Pascal Programming/Sets
This chapter introduces you to a new custom data type. Sets are one of the basic structured data types. When programming you will frequently find that some logic can be modeled with sets. Learning and mastering usage of sets is a key skill, since you will encounter them a lot in Pascal.
Basics
[edit | edit source]Notion
[edit | edit source]Sets are (possibly empty) aggregations of distinguishable objects. Either a set contains an object, or it does not. An object being part of a set is also referred to as element of that set.
Let's say we know the objects “apple”, “banana” and “pencil”. The set Fruit ≔ {“apple”, “banana”} contains the objects “apple” and “banana”. “Pencil” is not a member of the set Fruit.
Digitization
[edit | edit source]When a computer is supposed to store and process a set, it actually handles a series of Boolean values.[fn 1]
Every one of those Boolean values tells us whether a certain element is part of a set.
A computer does also store a Boolean value for every object that is not part of a certain set.
|
Sets in Pascal
[edit | edit source]The computer needs to know how many Boolean values it needs to set aside.
In order to achieve this, a set in Pascal requires an ordinal type as a set’s base type.
An ordinal type always has a finite range of permissible discrete values, thus the computer knows beforehand how many Boolean values to reserve, how many elements we can expect a set contain at most.
In consequence, a valid set type declaration is:
type
characters = set of char;
A variable of the data type characters can only contain char values.
This set cannot contain, for instance, 42, that is an integer value, nor is this information stored in any way.
A data type declaration for a set of real is illegal, since the set’s base type, the data type real, is not an ordinal data type.
Remember, in order to qualify as an ordinal data type there must be a means to assign every legal value an integer value.[fn 2] |
Sets are particularly useful in conjunction with enumeration data types, which you just learned in previous chapter. Let’s consider an example in Pascal:
program setDemo;
type
skill = (cooking, cleaning, driving, videogames, eating);
skills = set of skill;
var
slob: skills;
begin
slob := [videogames, eating];
end.
Here, we have declared a variable slob, which represents a set of the skill enumeration data type values.
In the penultimate line we populate our set slob with two objects, videogames and eating.
The brackets indicate a set literal.
[videogames, eating] is a set expression which we are assigning to the slob variable.
The set variable slob contains no other objects.
However, the computer still stores five Boolean values for every potential member of that set.
The number five is number of elements in skill, the set’s base type.
The information that cooking, cleaning and driving are not part of the set slob is stored explicitly (by the proper Boolean value false).
Inspecting a set
[edit | edit source]If we want to learn, whether a certain object is part of a set, the set operator in yields the corresponding Boolean value the computer uses to store that information.
program setInspection(output);
type
skill = (cooking, cleaning, driving, videogames, eating);
skills = set of skill;
var
slob: skills;
begin
slob := [videogames, eating];
if videogames in slob then
begin
writeLn('Is she a level 45 dungeon master?');
end;
end.
The in operator is one of Pascal’s non-commutative operators.
This means, you cannot swap the operands.
On the RHS you always need to write an expression evaluating to a set value, whereas the LHS has to be an expression evaluating to this set’s base type.
Even though we, as humans, can say that 42 in slob is wrong, i. e. false, such a comparison is illegal.
Per definition, the slob set can only contain skill values.
Operations
[edit | edit source]So far, sets probably seemed like a really complicated way for using Boolean values.
The true power of sets lies in a number of distinct operations, making sets an easier, and thus better alternative to handling two or more individual (but related) Boolean values directly.
Combinations
[edit | edit source]In Pascal, two sets of the same kind, the same data type, can be combined forming a new set of the respective data type. Following operators are available:
| name | mathematical symbol | source code symbol |
|---|---|---|
| union | ∪ | +
|
| difference | ∖ | -
|
| intersection | ∩ | *
|
| symmetric difference | △ | ><†
|
† The symmetric difference operator is only defined in EP.
Union
[edit | edit source]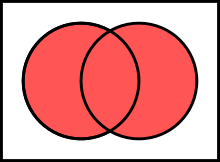
The result of unifying two sets into one is called union. Let’s say, recently our slob has learned how to drive and does that now too. This can be written as:
slob := slob + [driving];
Now, slob contains all objects it previously held, plus all objects from the other set, [driving].
Difference
[edit | edit source]
Of course sets can be deprived of a set of elements by using the difference operator, in source code written as -.
slob := slob - [];
This removes all objects present in the second set from the first set.
Here, the empty set ([]) does not contain any objects, thus removing no objects has virtually no effect on slob.
Intersection
[edit | edit source]
Furthermore you can intersect sets. The intersection of two sets is defined as the set of elements both operands contain.
program intersectionDemo;
type
skill = (cooking, cleaning, driving, videogames, eating);
skills = set of skill;
var
slob, blueCollar, common: skills;
begin
blueCollar := [cooking, cleaning, driving, eating];
slob := [driving, videogames, eating];
common := blueCollar * slob;
end.
The set common now (only) contains driving and eating, because those are the objects member of both operands, of both given sets.
Symmetric difference
[edit | edit source]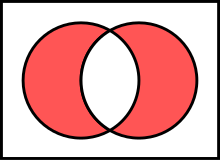
A disjunct result to the intersection gives the symmetric difference. It is the union of the operands without the elements contained in both sets.
unique := blueCollar >< slob;
Now unique is [cooking, cleaning, videogames], because those are the values from either set, but not both.
Comparisons
[edit | edit source]Two sets of the same kind, the same data type, can be compared by looking at each element in both sets.
| name | mathematical symbol | source code symbol |
|---|---|---|
| equality | = | =
|
| inequality | ≠ | <>
|
| inclusion | ⊆ | <=
|
| inclusion | ⊇ | >=
|
| element | ∈ | in
|
All comparison operators, as before, evaluate to a Boolean expression.
Inclusion
[edit | edit source]The inclusion of a two sets means that all objects one set contains are present in another set.
If the expression A <= B evaluates to true, all objects present in the set A are also present B.
In a Venn diagram you will notice that one circle’s area is completely surrounded by another circle, if not identical to the other circle.
Equality and inequality
[edit | edit source]The equality of two sets is defined as A <= B and B <= A.
All objects contained in the left-hand set are present in the right-hand set and vice versa.
In other words, there is not a single object that is present in just one of the sets.
The inequality is just the negation thereof.
Element of
[edit | edit source]The in operator is the only set operator that does not act on two sets but on one potential set member candidate and a set.
It has been introduced above.
With respect to Venn diagrams, though, you can say that the in operator is “like” pointing with your index finger to a point inside a circle, or outside of it.
Pre-defined set routines
[edit | edit source]Cardinality
[edit | edit source](After initialization) at any time a set contains a certain number of elements.
In mathematics the number of objects being part of a set is called cardinality.
The cardinality of a set can be retrieved using the function card, an EP extension.
emptySet := [];
writeLn(card(emptySet));
This will print 0 as there are no elements in an empty set.
Unfortunately, not all compilers implement the card function.
The FPC does not have none.
The GPC does supply one, though.
Universe
[edit | edit source]Originally, Wirth proposed a function all:
[1]
all(T)is the set of all values of type T
For example:
superwoman := all(skill);
The set superwoman would contain all available skill values, cooking, cleaning, driving, videogames, eating.
Unfortunately, this proposal never made it into the ISO standards, nor do the FPC or GPC support that function, or provide an equivalent.
The only alternative is to use an appropriate set constructor (an EP extension):
[cooking..eating] is equivalent to all(skill), provided that cooking is the first skill and eating the last skill value (referring to the order these items were listed during the data type declaration of skill).
Inclusion and exclusion
[edit | edit source]Not standardized, but convenient is BP’s definition of include and exclude procedures.
These are shorthand for very frequent set manipulations.
The procedures allow you to quickly add or remove one object from one set.
include(recognizedLetters, 'Z');
is identical to
recognizedLetters := recognizedLetters + ['Z'];
but you do not need to type out the set name twice and everything, thus reducing the chance of typing mistakes. Likewise,
exclude(primeSieve, 4);
will do the same as
primeSieve := primeSieve - [4];
Both, the FPC and GPC, support these handy routines, which are in fact in all cases implemented as compiler intrinsics, not actual procedures.
Intermediate usage
[edit | edit source]Set literals
[edit | edit source]Effectively stating sets is a required skill when handling sets.
It is important to understand that sets merely store the information that an object is a member of a set, or not.
The set ['A', 'A', 'A'] is identical to ['A'].
Specifying 'A' multiple times does not make it “more” part of that set.
Also, it is not necessary to list all members in any particular order.
['X', 'Z', 'Y'] is just as acceptable as ['X', 'Y', 'Z'] is.
Mathematically speaking, sets are not ordered.
Pascal’s requirement that a set’s base data type has to be an ordinal type is purely a technical requirement.
For readability reasons it is usually sensible, though, to list elements in ascending order.
The EP standard gives you nice short notation for set literals containing a continuous series of values.
Instead of writing [7, 8, 9, 11, 12, 13] you can also write ranges like [7..9, 11..13] evaluating to the very same value.
Of course, all numbers could also be variables, or expressions in general.
Set literals are always a positive statement which objects are in a set.
If we wanted a set of integer values between 0 and 10 without 3, 5 and 7, but do not want to write this set out entirely (i. e. as [0, 1, 2, 4, 6, 8, 9, 10]), you can either write [0..2, 4, 6, 8..10] or the expression [0..10] - [3, 5, 7].
The latter is probably a little easier to grasp what objects are and which are not in the final set.
Memory restrictions
[edit | edit source]Although a set of integer is legal and complies with all Pascal standards, many compilers do not support such large sets.
Per definition, a set of integer can contain (at most) all values in the range -maxInt..maxInt.
That is a lot (try writeLn(maxInt) or read your compiler’s documentation to find out this value).
On a 64‑bit platform this value (usually) is 263−1, i. e. 9,223,372,036,854,775,808.
As of the year 2020 many computers will quickly run out of main memory if they attempted to hold that many Boolean values.
As a consequence, BP restricts permissible set’s base types.
In BP the base type’s largest and smallest values’ ordinal values have to be in the range 0..255.
The value 255 is 28−1.
As of version 3.2.0, the FPC sets the same limitations.
The GPC allows set definitions beyond 28 elements, although some configuration is required:
You need to specify the ‑‑setlimit command-line parameter or a specially crafted comment in your source code:
program largeSetDemo;
{$setLimit=2147483647} // this is 2³¹ − 1
type
// 1073741823 is 2³⁰ − 1
characteristicInteger = -1073741823..1073741823;
integers = set of characteristicInteger;
var
manyManyIntegers: integers;
begin
manyManyIntegers := [];
include(manyManyIntegers, 1073741823);
end.
This will instruct the GPC that a set of characteristicInteger can only store up to this many characteristicInteger values.
Loops
[edit | edit source]Now that you have made the acquaintance of enumeration data types and sets, you see yourself faced with dealing a growing number of data. Pascal, like many other programming languages, support a language construct called loops.
Characteristics
[edit | edit source]Loops are (possibly empty) sequences of statements that are repeated over and over again, or even never, based on a Boolean value.
The sequence of statements is termed loop body.
The loop head contains (possibly implicitly) a Boolean expression determining whether the loop body is executed.
Every time the loop body is run, an iteration is in progress.
The term loop originates from the circumstance that some early models of computers required programs to be fed (“loaded”) via punched paper tape. If a portion of that paper tape was meant to be processed multiple times, that piece of paper tape was cut, bent and temporarily fixated so it formed a physical loop. Thankfully, advancements in computer technology has made it far more convenient to handle repeating code.
Pascal (and many other programming languages) differentiate between two groups of loops:
- counting loops, presented here, and
- conditional loops, presented in a chapter to come.
Counting loops have in common that, before running the first iteration it can already be determined how many times the loop body will be executed just by evaluating the loop head.[fn 3]
Conditional loops on the other hand are based on an abort condition, i. e. a Boolean expression.
Except for infinite loops, there is no way to tell in advance how many times, how many iterations a conditional loop will have without thoroughly (mathematically) analyzing the loop body and loop head, and possibly even considering circumstances beyond the loop.
Counting loops
[edit | edit source]Counting loops do not necessarily count a quantity. They are named after the fact that they employ a variable, a counting variable. This variable of any ordinal data type (de facto) assigns every iteration a number.
A counting loop is introduced by the reserved word for:
program forLoopDemo(output);
var
i: integer;
begin
for i := 1 to 10 do // loop head
begin // ┐
writeLn(i:3); // ┝ loop body
end; // ┘
end.
After for follows a specially crafted assignment to the counting variable.
Range of counting variable
[edit | edit source]1 to 10 (with the auxiliary reserved word to) denotes a range of values the counting variable i will assume while executing the loop body.
1 and 10 are both expressions possessing the counting variable’s data type, that means there could also appear variables or more complex expressions, not just constant literals as shown.
This range is like a set.
It may possibly be empty:
The range 5 to 4 is an empty range, since there are no values between 5 up to and including 4.
In consequence, the counting variable will not be assigned any value out of this empty range, as there simply are none available, and the loop body is never executed.
Nevertheless, the range 8 to 8 contains exactly one value, i. e. 8.
During the first iteration the corresponding counting variable, here i, will have the first value out of the given range, the start value, in the example above this is the value 1.
In the successive iteration the variable i has the value 2, and so forth up to and including the final value of the given range, here 10.
Immutability of counting variable
[edit | edit source]It is not necessary to actually utilize the counting variable inside the loop body, but you can use it if you are just obtaining its current value:
Inside the loop body of for‑loops it is forbidden to assign any values to the counting variable.
Forbidden assignments include, but are not limited to putting the counting the variable on the LHS of :=, but also read/readLn may not use the counting variable.
Tampering with the counting variable is forbidden, because the loop head will effectively employ succ(i) to obtain the next iteration’s value.
The loop head implicitly contains the Boolean expression counting variable ≠ final value.
If the counting variable was manipulated this condition might never be met, thus destroying the characteristics of a for‑loop.
Preventing the programmer to do any assignments preemptively ensures such an infinite loop is not, accidentally as well as deliberately, created.
Reverse direction
[edit | edit source]Pascal also allows for‑loops in a reversed direction using the reserved word downto instead of to:
program downtoDemo(output);
var
c: char;
begin
for c := 'Z' downto 'B' do
begin
write(c, ' ');
end;
writeLn('A');
end.
Here, the range is 'Z' down and including to 'B'.
The loop’s terminating condition is still counting variable ≠ final value, but in this case the counting variable c becomes pred(c) (not succ) at the end of each iteration, after the loop body has been executed.
Loops on collections
[edit | edit source]EP allows to iterate over discrete aggregations, such as sets. This is particularly useful if you have a routine that needs to be applied to every value of an aggregation. Here is an example to demonstrate the principle:
program forInDemo(output);
var
c: char;
vowels: set of char;
begin
vowels := ['A', 'E', 'I', 'O', 'U'];
for c in vowels do
begin
writeLn(c);
end;
end.
Now you see the word in again, but in this context c in vowels is not an expression.
The data type restrictions for in are still in effect:
On the RHS an aggregation expression is given, whereas the LHS is in this case a variable that has the aggregation’s data type.
This variable will be assigned every value out of the given aggregation every time an iteration is processed.
Since the RHS just needs an expression, not necessarily a variable, so you can shorten the example even further to:
for c in ['A', 'E', 'I', 'O', 'U'] do
Note, unlike the counting loops above, you are not supposed to make any assumptions about the order the loop variable is assigned values to.
It may be in ascending, descending, or completely mixed up “order”, but the specific order is “implementation defined”, i. e. it depends on the used compiler.
Accompanying documents of the compiler explain in which order the for … in loop is processed.
Tasks
[edit | edit source]fruit - fruit evaluate to?Sources:
- ↑ Wirth, Niklaus. The Programming Language Pascal (Revised Report ed.). p. 38.
{{cite book}}: Unknown parameter|month =ignored (help); Unknown parameter|year =ignored (help)
Notes:
- ↑ This is an analogy for explanation. The ISO standards do not set this requirement. Compiler developers are free to choose whatever implementation of the set data type they think is suitable. It would be perfectly OK to just store a list of elements that are present in a set and nothing else. Nevertheless, all, Delphi, FPC, as well as the GPC do store sets as a series of bits (“
Booleanvalues”) as it is explained here. - ↑ The data type
realdoes not qualify as an ordinal data type. Although it stores a finite subset of ℚ, the set of rational numbers, so there is a map ℚT ↦ ℕ, this depends on therealdata type’s precision (T), thus there is no one standard way of definingordforrealvalues, but many. - ↑ This statement ignores many dialects’ extensions
break/leave/continue/cyclethat neither the ISO standards 7185 (Standard Pascal) or 10206 (Extended Pascal) define, or thegotostatement.