Partial Differential Equations/Test functions

Motivation

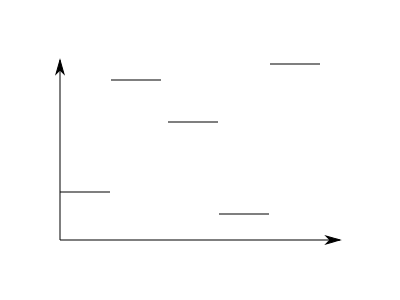
Before we dive deeply into the chapter, let's first motivate the notion of a test function. Let's consider two functions which are piecewise constant on the intervals $[0,1),[1,2),[2,3),[3,4),[4,5)$ and zero elsewhere; like, for example, these two:

Let's call the left function $f_{1}$, and the right function $f_{2}$.

Of course we can easily see that the two functions are different; they differ on the interval $[4,5)$; however, let's pretend that we are blind and our only way of finding out something about either function is evaluating the integrals

$\int _{\mathbb {R} }\varphi (x)f_{1}(x)dx$ and $\int _{\mathbb {R} }\varphi (x)f_{2}(x)dx$

for functions $\varphi$ in a given set of functions ${\mathcal {X}}$.

We proceed with choosing ${\mathcal {X}}$ sufficiently clever such that five evaluations of both integrals suffice to show that $f_{1}\neq f_{2}$. To do so, we first introduce the characteristic function. Let $A\subseteq \mathbb {R}$ be any set. The characteristic function of $A$ is defined as

$\chi _{A}(x):={\begin{cases}1&x\in A\\0&x\notin A\end{cases}}$

With this definition, we choose the set of functions ${\mathcal {X}}$ as

${\mathcal {X}}:=\{\chi _{[0,1)},\chi _{[1,2)},\chi _{[2,3)},\chi _{[3,4)},\chi _{[4,5)}\}$

It is easy to see (see exercise 1), that for $n\in \{1,2,3,4,5\}$, the expression

$\int _{\mathbb {R} }\chi _{[n-1,n)}(x)f_{1}(x)dx$

equals the value of $f_{1}$ on the interval $[n-1,n)$, and the same is true for $f_{2}$. But as both functions are uniquely determined by their values on the intervals $[n-1,n),n\in \{1,2,3,4,5\}$ (since they are zero everywhere else), we can implement the following equality test:

$f_{1}=f_{2}\Leftrightarrow \forall \varphi \in {\mathcal {X}}:\int _{\mathbb {R} }\varphi (x)f_{1}(x)dx=\int _{\mathbb {R} }\varphi (x)f_{2}(x)dx$

This obviously needs five evaluations of each integral, as $\#{\mathcal {X}}=5$.

Since we used the functions in ${\mathcal {X}}$ to test $f_{1}$ and $f_{2}$, we call them test functions. What we ask ourselves now is if this notion generalises from functions like $f_{1}$ and $f_{2}$, which are piecewise constant on certain intervals and zero everywhere else, to continuous functions. The following chapter shows that this is true.

Bump functions

In order to write down the definition of a bump function more shortly, we need the following two definitions:

Definition 3.1:

Let $B\subseteq \mathbb {R} ^{d}$, and let $f:B\to \mathbb {R}$. We say that $f$ is smooth if all the partial derivatives

$\partial _{\alpha }f,\alpha \in \mathbb {N} _{0}^{d}$

exist in all points of $B$ and are continuous. We write $f\in {\mathcal {C}}^{\infty }(B)$.

Definition 3.2:

Let $f:\mathbb {R} ^{d}\to \mathbb {R}$. We define the support of $f$, ${\text{supp }}f$, as follows:

${\text{supp }}f:={\overline {\{x\in \mathbb {R} ^{d}|f(x)\neq 0\}}}$

Now we are ready to define a bump function in a brief way:

Definition 3.3:

$\varphi :\mathbb {R} ^{d}\to \mathbb {R}$ is called a bump function iff $\varphi \in {\mathcal {C}}^{\infty }(\mathbb {R} ^{d})$ and ${\text{supp }}\varphi$ is compact. The set of all bump functions is denoted by ${\mathcal {D}}(O)$.

These two properties make the function really look like a bump, as the following example shows:

The standard mollifier $\eta$ in dimension $d=1$

Example 3.4: The standard mollifier $\eta$, given by

$\eta :\mathbb {R} ^{d}\to \mathbb {R} ,\eta (x)={\frac {1}{c}}{\begin{cases}e^{-{\frac {1}{1-\|x\|^{2}}}}&{\text{ if }}\|x\|_{2}<1\\0&{\text{ if }}\|x\|_{2}\geq 1\end{cases}}$

, where $c:=\int _{B_{1}(0)}e^{-{\frac {1}{1-\|x\|^{2}}}}dx$, is a bump function (see exercise 2).

Schwartz functions

As for the bump functions, in order to write down the definition of Schwartz functions shortly, we first need two helpful definitions.

Definition 3.5:

Let $X$ be an arbitrary set, and let $f:X\to \mathbb {R}$ be a function. Then we define the supremum norm of $f$ as follows:

$\|f\|_{\infty }:=\sup \limits _{x\in X}|f(x)|$

Definition 3.6:

For a vector $x=(x_{1},\ldots ,x_{d})\in \mathbb {R} ^{d}$ and a $d$-dimensional multiindex $\alpha \in \mathbb {N} _{0}^{d}$ we define $x^{\alpha }$, $x$ to the power of $\alpha$, as follows:

$x^{\alpha }:=x_{1}^{\alpha _{1}}\cdots x_{d}^{\alpha _{d}}$

Now we are ready to define a Schwartz function.

Definition 3.7:

We call $\phi :\mathbb {R} ^{d}\to \mathbb {R}$ a Schwartz function iff the following two conditions are satisfied:

1. $\phi \in {\mathcal {C}}^{\infty }(\mathbb {R} ^{d})$
2. $\forall \alpha ,\beta \in \mathbb {N} _{0}^{d}:\|x^{\alpha }\partial _{\beta }\phi \|_{\infty }<\infty$

By $x^{\alpha }\partial _{\beta }\phi$ we mean the function $x\mapsto x^{\alpha }\partial _{\beta }\phi (x)$.

$f(x,y)=e^{-x^{2}-y^{2}}$

Example 3.8: The function

$f:\mathbb {R} ^{2}\to \mathbb {R} ,f(x,y)=e^{-x^{2}-y^{2}}$

is a Schwartz function.

Theorem 3.9:

Every bump function is also a Schwartz function.

This means for example that the standard mollifier is a Schwartz function.

Proof:

Let $\varphi$ be a bump function. Then, by definition of a bump function, $\varphi \in {\mathcal {C}}^{\infty }(\mathbb {R} ^{d})$. By the definition of bump functions, we choose $R>0$ such that

${\text{supp }}\varphi \subseteq {\overline {B_{R}(0)}}$

, as in $\mathbb {R} ^{d}$, a set is compact iff it is closed & bounded. Further, for $\alpha ,\beta \in \mathbb {N} _{0}^{d}$ arbitrary,

${\begin{aligned}\|x^{\alpha }\partial _{\beta }\varphi (x)\|_{\infty }&:=\sup _{x\in \mathbb {R} ^{d}}|x^{\alpha }\partial _{\beta }\varphi (x)|&\\&=\sup _{x\in {\overline {B_{R}(0)}}}|x^{\alpha }\partial _{\beta }\varphi (x)|&{\text{supp }}\varphi \subseteq {\overline {B_{R}(0)}}\\&=\sup _{x\in {\overline {B_{R}(0)}}}\left(|x^{\alpha }||\partial _{\beta }\varphi (x)|\right)&{\text{rules for absolute value}}\\&\leq \sup _{x\in {\overline {B_{R}(0)}}}\left(R^{|\alpha |}|\partial _{\beta }\varphi (x)|\right)&\forall i\in \{1,\ldots ,d\},(x_{1},\ldots ,x_{d})\in {\overline {B_{R}(0)}}:|x_{i}|\leq R\\&<\infty &{\text{Extreme value theorem}}\end{aligned}}$

$\Box$

Convergence of bump and Schwartz functions

Now we define what convergence of a sequence of bump (Schwartz) functions to a bump (Schwartz) function means.

Definition 3.10:

A sequence of bump functions $(\varphi _{i})_{i\in \mathbb {N} }$ is said to converge to another bump function $\varphi$ iff the following two conditions are satisfied:

1. There is a compact set $K\subset \Omega$ such that $\forall i\in \mathbb {N} :{\text{supp }}\varphi _{i}\subseteq K$
2. $\forall \alpha \in \mathbb {N} _{0}^{d}:\lim _{i\rightarrow \infty }\|\partial _{\alpha }\varphi _{i}-\partial _{\alpha }\varphi \|_{\infty }=0$

Definition 3.11:

We say that the sequence of Schwartz functions $(\phi _{i})_{i\in \mathbb {N} }$ converges to $\phi$ iff the following condition is satisfied:

$\forall \alpha ,\beta \in \mathbb {N} _{0}^{d}:\|x^{\alpha }\partial _{\beta }\phi _{i}-x^{\alpha }\partial _{\beta }\phi \|_{\infty }\to 0,i\to \infty$

Theorem 3.12:

Let $(\varphi _{i})_{i\in \mathbb {N} }$ be an arbitrary sequence of bump functions. If $\varphi _{i}\to \varphi$ with respect to the notion of convergence for bump functions, then also $\varphi _{i}\to \varphi$ with respect to the notion of convergence for Schwartz functions.

Proof:

Let $O\subseteq \mathbb {R} ^{d}$ be open, and let $(\varphi _{l})_{l\in \mathbb {N} }$ be a sequence in ${\mathcal {D}}(O)$ such that $\varphi _{l}\to \varphi \in {\mathcal {D}}(O)$ with respect to the notion of convergence of ${\mathcal {D}}(O)$. Let thus $K\subset \mathbb {R} ^{d}$ be the compact set in which all the ${\text{supp }}\varphi _{l}$ are contained. From this also follows that ${\text{supp }}\varphi \subseteq K$, since otherwise $\|\varphi _{l}-\varphi \|_{\infty }\geq |c|$, where $c\in \mathbb {R}$ is any nonzero value $\varphi$ takes outside $K$; this would contradict $\varphi _{l}\to \varphi$ with respect to our notion of convergence.

In $\mathbb {R} ^{d}$, ‘compact’ is equivalent to ‘bounded and closed’. Therefore, $K\subset B_{R}(0)$ for an $R>0$. Therefore, we have for all multiindices $\alpha ,\beta \in \mathbb {N} _{0}^{d}$:

${\begin{aligned}\|x^{\alpha }\partial _{\beta }\varphi _{l}-x^{\alpha }\partial _{\beta }\varphi \|_{\infty }&=\sup _{x\in \mathbb {R} ^{d}}\left|x^{\alpha }\partial _{\beta }\varphi _{l}(x)-x^{\alpha }\partial _{\beta }\varphi (x)\right|&{\text{ definition of the supremum norm}}\\&=\sup _{x\in B_{R}(0)}\left|x^{\alpha }\partial _{\beta }\varphi _{l}(x)-x^{\alpha }\partial _{\beta }\varphi (x)\right|&{\text{ as }}{\text{supp }}\varphi _{l},{\text{supp }}\varphi \subseteq K\subset B_{R}(0)\\&\leq R^{|\alpha |}\sup _{x\in B_{R}(0)}\left|\partial _{\beta }\varphi _{l}(x)-\partial _{\beta }\varphi (x)\right|&\forall i\in \{1,\ldots ,d\},(x_{1},\ldots ,x_{d})\in {\overline {B_{R}(0)}}:|x_{i}|\leq R\\&=R^{|\alpha |}\sup _{x\in \mathbb {R} ^{d}}\left|\partial _{\beta }\varphi _{l}(x)-\partial _{\beta }\varphi (x)\right|&{\text{ as }}{\text{supp }}\varphi _{l},{\text{supp }}\varphi \subseteq K\subset B_{R}(0)\\&=R^{|\alpha |}\left\|\partial _{\beta }\varphi _{l}(x)-\partial _{\beta }\varphi (x)\right\|_{\infty }&{\text{ definition of the supremum norm}}\\&\to 0,l\to \infty &{\text{ since }}\varphi _{l}\to \varphi {\text{ in }}{\mathcal {D}}(O)\end{aligned}}$

Therefore the sequence converges with respect to the notion of convergence for Schwartz functions.$\Box$

The ‘testing’ property of test functions

In this section, we want to show that we can test equality of continuous functions $f,g$ by evaluating the integrals

$\int _{\mathbb {R} ^{d}}f(x)\varphi (x)dx$ and $\int _{\mathbb {R} ^{d}}g(x)\varphi (x)dx$

for all $\varphi \in {\mathcal {D}}(O)$ (thus, evaluating the integrals for all $\varphi \in {\mathcal {S}}(\mathbb {R} ^{d})$ will also suffice as ${\mathcal {D}}(O)\subset {\mathcal {S}}(\mathbb {R} ^{d})$ due to theorem 3.9).

But before we are able to show that, we need a modified mollifier, where the modification is dependent of a parameter, and two lemmas about that modified mollifier.

Definition 3.13:

For $R\in \mathbb {R} _{>0}$, we define

$\eta _{R}:\mathbb {R} ^{d}\to \mathbb {R} ,\eta _{R}(x)=\eta \left({\frac {x}{R}}\right){\big /}R^{d}$.

Lemma 3.14:

Let $R\in \mathbb {R} _{>0}$. Then

${\text{supp }}\eta _{R}={\overline {B_{R}(0)}}$.

Proof:

From the definition of $\eta$ follows

${\text{supp }}\eta ={\overline {B_{1}(0)}}$.

Further, for $R\in \mathbb {R} _{>0}$

${\begin{aligned}{\frac {x}{R}}\in {\overline {B_{1}(0)}}&\Leftrightarrow \left\|{\frac {x}{R}}\right\|\leq 1\\&\Leftrightarrow \|x\|\leq R\\&\Leftrightarrow x\in {\overline {B_{R}(0)}}\end{aligned}}$

Therefore, and since

$x\in {\text{supp }}\eta _{R}\Leftrightarrow {\frac {x}{R}}\in {\text{supp }}\eta$

, we have:

$x\in {\text{supp }}\eta _{R}\Leftrightarrow x\in {\overline {B_{R}(0)}}$$\Box$

In order to prove the next lemma, we need the following theorem from integration theory:

Theorem 3.15: (Multi-dimensional integration by substitution)

If $O,U\subseteq \mathbb {R} ^{d}$ are open, and $\psi :U\to O$ is a diffeomorphism, then

$\int _{O}f(x)dx=\int _{U}f(\psi (x))|\det J_{\psi }(x)|dx$

We will omit the proof, as understanding it is not very important for understanding this wikibook.

Lemma 3.16:

Let $R\in \mathbb {R} _{>0}$. Then

$\int _{\mathbb {R} ^{d}}\eta _{R}(x)dx=1$.

Proof:

${\begin{aligned}\int _{\mathbb {R} ^{d}}\eta _{R}(x)dx&=\int _{\mathbb {R} ^{d}}\eta \left({\frac {x}{R}}\right){\big /}R^{d}dx&{\text{Def. of }}\eta _{R}\\&=\int _{\mathbb {R} ^{d}}\eta (x)dx&{\text{integration by substitution using }}x\mapsto Rx\\&=\int _{B_{1}(0)}\eta (x)dx&{\text{Def. of }}\eta \\&={\frac {\int _{B_{1}(0)}e^{-{\frac {1}{1-\|x\|}}}dx}{\int _{B_{1}(0)}e^{-{\frac {1}{1-\|x\|}}}dx}}&{\text{Def. of }}\eta \\&=1\end{aligned}}$$\Box$

Now we are ready to prove the ‘testing’ property of test functions:

Theorem 3.17:

Let $f,g:\mathbb {R} ^{d}\to \mathbb {R}$ be continuous. If

$\forall \varphi \in {\mathcal {D}}(O):\int _{\mathbb {R} ^{d}}\varphi (x)f(x)dx=\int _{\mathbb {R} ^{d}}\varphi (x)g(x)dx$,

then $f=g$.

Proof:

Let $x\in \mathbb {R} ^{d}$ be arbitrary, and let $\epsilon \in \mathbb {R} _{>0}$. Since $f$ is continuous, there exists a $\delta \in \mathbb {R} _{>0}$ such that

$\forall y\in {\overline {B_{\delta }(x)}}:|f(x)-f(y)|<\epsilon$

Then we have

${\begin{aligned}\left|f(x)-\int _{\mathbb {R} ^{d}}f(y)\eta _{\delta }(x-y)dy\right|&=\left|\int _{\mathbb {R} ^{d}}(f(x)-f(y))\eta _{\delta }(x-y)dy\right|&{\text{lemma 3.16}}\\&\leq \int _{\mathbb {R} ^{d}}|f(x)-f(y)|\eta _{\delta }(x-y)dy&{\text{triangle ineq. for the }}\int {\text{ and }}\eta _{\delta }\geq 0\\&=\int _{\overline {B_{\delta }(0)}}|f(x)-f(y)|\eta _{\delta }(x-y)dy&{\text{lemma 3.14}}\\&\leq \int _{\overline {B_{\delta }(0)}}\epsilon \eta _{\delta }(x-y)dy&{\text{monotony of the }}\int \\&\leq \epsilon &{\text{lemma 3.16 and }}\eta _{\delta }\geq 0\end{aligned}}$

Therefore, $\int _{\mathbb {R} ^{d}}f(y)\eta _{\delta }(x-y)dy\to f(x),\delta \to 0$. An analogous reasoning also shows that $\int _{\mathbb {R} ^{d}}g(y)\eta _{\delta }(x-y)dy\to g(x),\delta \to 0$. But due to the assumption, we have

$\forall \delta \in \mathbb {R} _{>0}:\int _{\mathbb {R} ^{d}}g(y)\eta _{\delta }(x-y)dy=\int _{\mathbb {R} ^{d}}f(y)\eta _{\delta }(x-y)dy$

As limits in the reals are unique, it follows that $f(x)=g(x)$, and since $x\in \mathbb {R} ^{d}$ was arbitrary, we obtain $f=g$.$\Box$

Remark 3.18: Let $f,g:\mathbb {R} ^{d}\to \mathbb {R}$ be continuous. If

$\forall \varphi \in {\mathcal {S}}(\mathbb {R} ^{d}):\int _{\mathbb {R} ^{d}}\varphi (x)f(x)dx=\int _{\mathbb {R} ^{d}}\varphi (x)g(x)dx$,

then $f=g$.

Proof:

This follows from all bump functions being Schwartz functions, which is why the requirements for theorem 3.17 are met.$\Box$

Exercises

1. Let $b\in \mathbb {R}$ and $f:\mathbb {R} \to \mathbb {R}$ be constant on the interval $[b-1,b)$. Show that

   $\forall y\in [b-1,b):\int _{\mathbb {R} }\chi _{[b-1,b)}(x)f(x)dx=f(y)$

2. Prove that the standard mollifier as defined in example 3.4 is a bump function by proceeding as follows:

   1. Prove that the function

      $x\mapsto {\begin{cases}e^{-{\frac {1}{x}}}&x>0\\0&x\leq 0\end{cases}}$

      is contained in ${\mathcal {C}}^{\infty }(\mathbb {R} )$.

   2. Prove that the function

      $x\mapsto 1-\|x\|$

      is contained in ${\mathcal {C}}^{\infty }(\mathbb {R} ^{d})$.

   3. Conclude that $\eta \in {\mathcal {C}}^{\infty }(\mathbb {R} ^{d})$.
   4. Prove that ${\text{supp }}\eta$ is compact by calculating ${\text{supp }}\eta$ explicitly.
3. Let $O\subseteq \mathbb {R} ^{d}$ be open, let $\varphi \in {\mathcal {D}}(O)$ and let $\phi \in {\mathcal {S}}(\mathbb {R} ^{d})$. Prove that if $\alpha ,\beta \in \mathbb {N} _{0}^{d}$, then $\partial _{\alpha }\varphi \in {\mathcal {D}}(O)$ and $x^{\alpha }\partial _{\beta }\phi \in {\mathcal {S}}(\mathbb {R} ^{d})$.
4. Let $O\subseteq \mathbb {R} ^{d}$ be open, let $\varphi _{1},\ldots ,\varphi _{n}\in {\mathcal {D}}(O)$ be bump functions and let $c_{1},\ldots ,c_{n}\in \mathbb {R}$. Prove that $\sum _{j=1}^{n}c_{j}\varphi _{j}\in {\mathcal {D}}(O)$.
5. Let $\phi _{1},\ldots ,\phi _{n}$ be Schwartz functions functions and let $c_{1},\ldots ,c_{n}\in \mathbb {R}$. Prove that $\sum _{j=1}^{n}c_{j}\phi _{j}$ is a Schwartz function.
6. Let $\alpha \in \mathbb {N} _{0}^{d}$, let $p(x):=\sum _{\varsigma \leq \alpha }c_{\varsigma }x^{\varsigma }$ be a polynomial, and let $\phi _{l}\to \phi$ in the sense of Schwartz functions. Prove that $p\phi _{l}\to p\phi$ in the sense of Schwartz functions.