Given a point on an elastic body with stress state
σ
{\textstyle {\boldsymbol {\sigma }}}
σ
=
(
72
21
0
21
32
0
0
0
0
)
{\displaystyle {\boldsymbol {\sigma }}={\begin{pmatrix}72&21&0\\21&32&0\\0&0&0\end{pmatrix}}}
We're going to solve this by two methods. First using the analytic solution then using Mohr's circle.
We have the equations
σ
11
′
=
σ
11
+
σ
22
2
+
σ
11
−
σ
22
2
c
o
s
(
2
θ
)
+
σ
12
s
i
n
(
2
θ
)
σ
22
′
=
σ
11
+
σ
22
2
−
σ
11
−
σ
22
2
c
o
s
(
2
θ
)
−
σ
12
s
i
n
(
2
θ
)
{\displaystyle {\begin{aligned}\sigma '_{11}={\frac {\sigma _{11}+\sigma _{22}}{2}}+{\frac {\sigma _{11}-\sigma _{22}}{2}}cos\left(2\theta \right)+\sigma _{12}sin\left(2\theta \right)\\\sigma '_{22}={\frac {\sigma _{11}+\sigma _{22}}{2}}-{\frac {\sigma _{11}-\sigma _{22}}{2}}cos\left(2\theta \right)-\sigma _{12}sin\left(2\theta \right)\end{aligned}}}
and
σ
12
′
=
σ
22
−
σ
11
2
s
i
n
(
2
θ
)
+
σ
12
c
o
s
(
2
θ
)
{\displaystyle {\begin{aligned}\sigma '_{12}={\frac {\sigma _{22}-\sigma _{11}}{2}}sin\left(2\theta \right)+\sigma _{12}cos\left(2\theta \right)\end{aligned}}}
where the prime stresses are in the rotated reference frame.
When
σ
12
′
=
0
{\displaystyle \sigma '_{12}=0}
σ
11
′
=
σ
p
1
{\displaystyle \sigma '_{11}=\sigma _{p1}}
σ
22
′
=
σ
p
2
{\displaystyle \sigma '_{22}=\sigma _{p2}}
σ
12
′
=
0
{\displaystyle \sigma '_{12}=0}
t
a
n
(
2
θ
)
=
2
σ
12
σ
22
−
σ
11
{\displaystyle tan\left(2\theta \right)={\frac {2\sigma _{12}}{\sigma _{22}-\sigma _{11}}}}
and upon substituting the stresses given in this problem we find
θ
=
23.2
{\displaystyle \theta =23.2}
θ
{\displaystyle \theta }
σ
{\displaystyle {\boldsymbol {\sigma }}}
σ
11
′
=
σ
p
1
=
81
{\displaystyle \sigma '_{11}=\sigma _{p1}=81}
σ
22
′
=
σ
p
2
=
23
{\displaystyle \sigma '_{22}=\sigma _{p2}=23}
σ
12
′
=
0
{\displaystyle \sigma '_{12}=0}
If we are given a stress state that is the principal orientation then in our rotated reference frame above
σ
′
{\displaystyle {\boldsymbol {\sigma '}}}
σ
12
{\displaystyle \sigma _{12}}
σ
12
′
{\displaystyle \sigma '_{12}}
θ
{\displaystyle \theta }
d
σ
12
′
d
θ
=
d
d
θ
(
σ
22
−
σ
11
2
s
i
n
(
2
θ
)
)
=
(
σ
22
−
σ
11
)
c
o
s
(
2
θ
)
{\displaystyle {\frac {d\sigma '_{12}}{d\theta }}={\frac {d}{d\theta }}\left({\frac {\sigma _{22}-\sigma _{11}}{2}}sin\left(2\theta \right)\right)=\left(\sigma _{22}-\sigma _{11}\right)cos\left(2\theta \right)}
and the maximum occurs when
θ
=
45
{\displaystyle \theta =45}
23.2
+
45
=
68.2
{\displaystyle 23.2+45=68.2}
σ
{\displaystyle {\boldsymbol {\sigma }}}
σ
11
′
=
σ
p
1
=
52
{\displaystyle \sigma '_{11}=\sigma _{p1}=52}
σ
22
′
=
σ
p
2
=
52
{\displaystyle \sigma '_{22}=\sigma _{p2}=52}
σ
12
′
=
−
29
{\displaystyle \sigma '_{12}=-29}
90
{\displaystyle 90}
σ
11
′
=
σ
p
1
=
52
{\displaystyle \sigma '_{11}=\sigma _{p1}=52}
σ
22
′
=
σ
p
2
=
52
{\displaystyle \sigma '_{22}=\sigma _{p2}=52}
σ
12
′
=
29
{\displaystyle \sigma '_{12}=29}
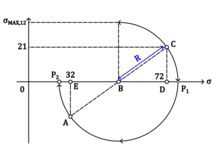
Diagram showing the Mohr's circle representation of this example problem. Following the diagram given here,
R
a
d
i
u
s
=
A
B
=
B
C
=
B
D
2
+
C
D
2
{\displaystyle Radius=AB=BC={\sqrt {BD^{2}+CD^{2}}}}
and
t
a
n
(
2
θ
)
=
C
D
B
D
{\displaystyle tan\left(2\theta \right)={\frac {CD}{BD}}}
Given
C
D
=
21
{\displaystyle CD=21}
O
D
=
72
{\displaystyle OD=72}
O
E
=
32
{\displaystyle OE=32}
A
D
=
40
{\displaystyle AD=40}
E
B
=
B
D
=
20
{\displaystyle EB=BD=20}
R
a
d
i
u
s
=
29
{\displaystyle Radius=29}
θ
=
23.2
{\displaystyle \theta =23.2}
P
1
=
O
B
+
R
a
d
i
u
s
=
O
E
+
E
B
+
R
a
d
i
u
s
=
81
{\displaystyle P1=OB+Radius=OE+EB+Radius=81}
P
2
=
P
1
−
2
R
a
d
i
u
s
=
23
{\displaystyle P2=P1-2Radius=23}
±
R
a
d
i
u
s
=
±
29
{\displaystyle \pm Radius=\pm 29}
23.2
+
45
=
68.2
{\displaystyle 23.2+45=68.2}
23.2
+
45
+
90
=
158.2
=
−
21.8
∘
{\displaystyle 23.2+45+90=158.2=-21.8^{\circ }}
Given a point on an elastic body with stress state
σ
{\textstyle {\boldsymbol {\sigma }}}
σ
=
(
0
6
8
6
0
10
8
10
0
)
{\displaystyle {\boldsymbol {\sigma }}={\begin{pmatrix}0&6&8\\6&0&10\\8&10&0\end{pmatrix}}}
Given a point on an elastic body with stress state
σ
{\textstyle {\boldsymbol {\sigma }}}
x
3
{\textstyle x_{3}}
σ
′
{\textstyle {\boldsymbol {\sigma '}}}
q
{\textstyle q}
σ
=
(
25
q
σ
12
0
σ
21
5
q
0
0
0
0
)
σ
′
=
(
50
5
0
5
σ
22
′
0
0
0
0
)
{\displaystyle {\boldsymbol {\sigma }}={\begin{pmatrix}25q&\sigma _{12}&0\\\sigma _{21}&5q&0\\0&0&0\end{pmatrix}}~{\boldsymbol {\sigma '}}={\begin{pmatrix}50&5&0\\5&\sigma '_{22}&0\\0&0&0\end{pmatrix}}}
Diagram showing the Mohr's circle representation of this example problem. The shaded regions are similar triangles. We have the equations
σ
11
′
=
σ
11
+
σ
22
2
+
σ
11
−
σ
22
2
c
o
s
(
2
θ
)
+
σ
12
s
i
n
(
2
θ
)
σ
22
′
=
σ
11
+
σ
22
2
−
σ
11
−
σ
22
2
c
o
s
(
2
θ
)
−
σ
12
s
i
n
(
2
θ
)
{\displaystyle {\begin{aligned}\sigma '_{11}={\frac {\sigma _{11}+\sigma _{22}}{2}}+{\frac {\sigma _{11}-\sigma _{22}}{2}}cos\left(2\theta \right)+\sigma _{12}sin\left(2\theta \right)\\\sigma '_{22}={\frac {\sigma _{11}+\sigma _{22}}{2}}-{\frac {\sigma _{11}-\sigma _{22}}{2}}cos\left(2\theta \right)-\sigma _{12}sin\left(2\theta \right)\end{aligned}}}
and
σ
12
′
=
σ
22
−
σ
11
2
s
i
n
(
2
θ
)
+
σ
12
c
o
s
(
2
θ
)
{\displaystyle {\begin{aligned}\sigma '_{12}={\frac {\sigma _{22}-\sigma _{11}}{2}}sin\left(2\theta \right)+\sigma _{12}cos\left(2\theta \right)\end{aligned}}}
where the prime stresses are in the rotated reference frame.
This immediately allows us to substitute for
σ
12
′
{\displaystyle \sigma '_{12}}
θ
{\displaystyle \theta }
q
=
−
1
/
2
{\displaystyle q=-1/2}
σ
11
=
−
12.5
{\displaystyle \sigma _{11}=-12.5}
σ
22
=
−
2.5
{\displaystyle \sigma _{22}=-2.5}
σ
11
+
σ
22
+
σ
33
=
I
1
{\displaystyle \sigma _{11}+\sigma _{22}+\sigma _{33}=I_{1}}
allows
σ
11
+
σ
22
+
σ
33
=
σ
11
′
+
σ
22
′
+
σ
33
′
{\displaystyle \sigma _{11}+\sigma _{22}+\sigma _{33}=\sigma '_{11}+\sigma '_{22}+\sigma '_{33}}
with substitutions determines
σ
22
′
=
−
65
{\displaystyle \sigma '_{22}=-65}
σ
12
{\displaystyle \sigma _{12}}
σ
11
′
{\displaystyle \sigma '_{11}}
σ
22
′
{\displaystyle \sigma '_{22}}
σ
12
=
57.5
{\displaystyle \sigma _{12}=57.5}
σ
=
(
−
12.5
57.5
0
57.5
−
2.5
0
0
0
0
)
σ
′
=
(
50
5
0
5
−
65
0
0
0
0
)
{\displaystyle {\boldsymbol {\sigma }}={\begin{pmatrix}-12.5&57.5&0\\57.5&-2.5&0\\0&0&0\end{pmatrix}}~{\boldsymbol {\sigma '}}={\begin{pmatrix}50&5&0\\5&-65&0\\0&0&0\end{pmatrix}}}
The Mohr's circle representation of this solution is shown here. Note that the shaded triangles are similar and therefore can be used to simplify the solution if sought graphically.
Given a point on an elastic body with stress state
σ
{\textstyle {\boldsymbol {\sigma }}}
σ
=
(
18
12
9
12
12
−
6
9
−
6
6
)
{\displaystyle {\boldsymbol {\sigma }}={\begin{pmatrix}18&12&9\\12&12&-6\\9&-6&6\end{pmatrix}}}
Both mathematically and with words explain the impact of applying the transformation tensors
T
1
{\textstyle {\boldsymbol {T_{1}}}}
T
2
{\textstyle {\boldsymbol {T_{2}}}}
T
3
{\textstyle {\boldsymbol {T_{3}}}}
T
4
{\textstyle {\boldsymbol {T_{4}}}}
a
{\textstyle {\boldsymbol {a}}}
Z
{\textstyle {\boldsymbol {Z}}}
T
1
=
(
1
0
0
0
1
0
0
0
1
)
T
2
=
(
−
1
0
0
0
−
1
0
0
0
−
1
)
T
3
=
(
−
1
0
0
0
1
0
0
0
−
1
)
T
4
=
(
c
o
s
(
θ
)
0
s
i
n
(
θ
)
0
1
0
−
s
i
n
(
θ
)
0
c
o
s
(
θ
)
)
{\displaystyle {\boldsymbol {T_{1}}}={\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}}~{\boldsymbol {T_{2}}}={\begin{pmatrix}-1&0&0\\0&-1&0\\0&0&-1\end{pmatrix}}~{\boldsymbol {T_{3}}}={\begin{pmatrix}-1&0&0\\0&1&0\\0&0&-1\end{pmatrix}}~{\boldsymbol {T_{4}}}={\begin{pmatrix}cos\left(\theta \right)&0&sin\left(\theta \right)\\0&1&0\\-sin\left(\theta \right)&0&cos\left(\theta \right)\end{pmatrix}}}
a
=
(
a
1
a
2
a
3
)
Z
=
(
Z
11
Z
12
Z
13
Z
21
Z
22
Z
23
Z
31
Z
32
Z
33
)
{\displaystyle {\boldsymbol {a}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}~{\boldsymbol {Z}}={\begin{pmatrix}Z_{11}&Z_{12}&Z_{13}\\Z_{21}&Z_{22}&Z_{23}\\Z_{31}&Z_{32}&Z_{33}\end{pmatrix}}}
Remembering the definition of tensor multiplication and the implicit summations used in Einstein notation, we know that the rank two
T
{\displaystyle {\boldsymbol {T}}}
a
{\displaystyle {\boldsymbol {a}}}
a
2
′
=
a
1
T
11
+
a
2
T
12
+
a
3
T
13
{\displaystyle a'_{2}=a_{1}T_{11}+a_{2}T_{12}+a_{3}T_{13}}
which is similar to "normal" matrix multiplication as you've seen before.
In contrast applying the rank two transformation tensor on the rank two
Z
{\displaystyle {\boldsymbol {Z}}}
Z
12
′
=
T
11
T
21
Z
11
+
T
11
T
22
Z
12
+
T
11
T
23
Z
13
+
T
12
T
21
Z
21
+
T
12
T
22
Z
22
+
T
12
T
23
Z
23
+
T
13
T
21
Z
31
+
T
13
T
22
Z
32
+
T
13
T
23
Z
33
{\displaystyle Z'_{12}=T_{11}T_{21}Z_{11}+T_{11}T_{22}Z_{12}+T_{11}T_{23}Z_{13}+T_{12}T_{21}Z_{21}+T_{12}T_{22}Z_{22}+T_{12}T_{23}Z_{23}+T_{13}T_{21}Z_{31}+T_{13}T_{22}Z_{32}+T_{13}T_{23}Z_{33}}
When working with these type of 9-term sums it is usually advisable to use a software package to simply the work.
The results are given here.
Transformation tensor 1 results in
a
′
=
(
a
1
a
2
a
3
)
Z
′
=
(
Z
11
Z
12
Z
13
Z
21
Z
22
Z
23
Z
31
Z
32
Z
33
)
{\displaystyle {\boldsymbol {a'}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}~{\boldsymbol {Z'}}={\begin{pmatrix}Z_{11}&Z_{12}&Z_{13}\\Z_{21}&Z_{22}&Z_{23}\\Z_{31}&Z_{32}&Z_{33}\end{pmatrix}}}
which corresponds to the identity transformation, i.e., leave the tensors unmodified.
Transformation tensor 2 results in
a
′
=
(
−
a
1
−
a
2
−
a
3
)
Z
′
=
(
Z
11
Z
12
Z
13
Z
21
Z
22
Z
23
Z
31
Z
32
Z
33
)
{\displaystyle {\boldsymbol {a'}}={\begin{pmatrix}-a_{1}\\-a_{2}\\-a_{3}\end{pmatrix}}~{\boldsymbol {Z'}}={\begin{pmatrix}Z_{11}&Z_{12}&Z_{13}\\Z_{21}&Z_{22}&Z_{23}\\Z_{31}&Z_{32}&Z_{33}\end{pmatrix}}}
This transformation is the inversion transformation. This can be seen in the behavior of the vector. Interestingly enough it leaves
Z
{\displaystyle {\boldsymbol {Z}}}
Transformation tensor 3 results in
a
′
=
(
−
a
1
a
2
−
a
3
)
Z
′
=
(
Z
11
−
Z
12
Z
13
−
Z
21
Z
22
−
Z
23
Z
31
−
Z
32
Z
33
)
{\displaystyle {\boldsymbol {a'}}={\begin{pmatrix}-a_{1}\\a_{2}\\-a_{3}\end{pmatrix}}~{\boldsymbol {Z'}}={\begin{pmatrix}Z_{11}&-Z_{12}&Z_{13}\\-Z_{21}&Z_{22}&-Z_{23}\\Z_{31}&-Z_{32}&Z_{33}\end{pmatrix}}}
This transformation involves mirroring across the
x
1
{\displaystyle x_{1}}
x
3
{\displaystyle x_{3}}
x
2
{\displaystyle x_{2}}
180
{\displaystyle 180}
Transformation tensor 4 results in
a
′
=
(
a
1
c
o
s
(
θ
)
+
a
3
s
i
n
(
θ
)
a
2
a
3
c
o
s
(
θ
)
−
a
1
s
i
n
(
θ
)
)
Z
′
=
(
Z
11
c
o
s
(
θ
)
2
+
Z
13
c
o
s
(
θ
)
s
i
n
(
θ
)
+
Z
31
c
o
s
(
θ
)
s
i
n
(
θ
)
+
Z
33
s
i
n
(
θ
)
2
Z
12
c
o
s
(
θ
)
+
Z
32
s
i
n
(
θ
)
Z
13
c
o
s
(
θ
)
2
−
Z
11
c
o
s
(
θ
)
s
i
n
(
θ
)
+
Z
33
c
o
s
(
θ
)
s
i
n
(
θ
)
−
Z
31
s
i
n
(
θ
)
2
Z
21
c
o
s
(
θ
)
+
Z
23
s
i
n
(
θ
)
Z
22
Z
23
c
o
s
(
θ
)
−
Z
21
s
i
n
(
θ
)
Z
31
c
o
s
(
θ
)
2
−
Z
11
c
o
s
(
θ
)
s
i
n
(
θ
)
+
Z
33
c
o
s
(
θ
)
s
i
n
(
θ
)
−
Z
13
s
i
n
(
θ
)
2
Z
32
c
o
s
(
θ
)
−
Z
12
s
i
n
(
θ
)
Z
33
c
o
s
(
θ
)
2
−
Z
13
c
o
s
(
θ
)
s
i
n
(
θ
)
−
Z
31
c
o
s
(
θ
)
s
i
n
(
θ
)
+
Z
11
s
i
n
(
θ
)
2
)
{\displaystyle {\boldsymbol {a'}}={\begin{pmatrix}a_{1}cos\left(\theta \right)+a_{3}sin\left(\theta \right)\\a_{2}\\a3cos\left(\theta \right)-a_{1}sin\left(\theta \right)\end{pmatrix}}~{\boldsymbol {Z'}}={\begin{pmatrix}Z_{11}cos\left(\theta \right)^{2}+Z_{13}cos\left(\theta \right)sin\left(\theta \right)+Z_{31}cos\left(\theta \right)sin\left(\theta \right)+Z_{33}sin\left(\theta \right)^{2}&Z_{12}cos\left(\theta \right)+Z_{32}sin\left(\theta \right)&Z_{13}cos\left(\theta \right)^{2}-Z_{11}cos\left(\theta \right)sin\left(\theta \right)+Z_{33}cos\left(\theta \right)sin\left(\theta \right)-Z_{31}sin\left(\theta \right)^{2}\\Z_{21}cos\left(\theta \right)+Z_{23}sin\left(\theta \right)&Z_{22}&Z_{23}cos\left(\theta \right)-Z_{21}sin\left(\theta \right)\\Z_{31}cos\left(\theta \right)^{2}-Z_{11}cos\left(\theta \right)sin\left(\theta \right)+Z_{33}cos\left(\theta \right)sin\left(\theta \right)-Z_{13}sin\left(\theta \right)^{2}&Z_{32}cos\left(\theta \right)-Z_{12}sin\left(\theta \right)&Z_{33}cos\left(\theta \right)^{2}-Z_{13}cos\left(\theta \right)sin\left(\theta \right)-Z_{31}cos\left(\theta \right)sin\left(\theta \right)+Z_{11}sin\left(\theta \right)^{2}\end{pmatrix}}}
x
2
{\displaystyle x_{2}}
180
{\displaystyle 180}
θ
{\displaystyle \theta }
Consider the stress state
σ
{\textstyle {\boldsymbol {\sigma }}}
σ
=
(
72
21
0
21
32
0
0
0
0
)
{\displaystyle {\boldsymbol {\sigma }}={\begin{pmatrix}72&21&0\\21&32&0\\0&0&0\end{pmatrix}}}
We know from Example 1 that the solution is to rotate by
θ
=
23.2
{\displaystyle \theta =23.2}
x
3
{\displaystyle x_{3}}
σ
=
(
c
o
s
(
θ
)
s
i
n
(
θ
)
0
s
i
n
(
θ
)
c
o
s
(
θ
)
0
0
0
0
)
{\displaystyle {\boldsymbol {\sigma }}={\begin{pmatrix}cos\left(\theta \right)&sin\left(\theta \right)&0\\sin\left(\theta \right)&cos\left(\theta \right)&0\\0&0&0\end{pmatrix}}}
where
θ
=
23.2
{\displaystyle \theta =23.2}
Given the displacement tensor
e
{\textstyle {\boldsymbol {e}}}
e
=
(
0.001
0.001
0.002
−
0.001
0.002
0.002
0.001
0.003
0.002
)
{\displaystyle {\boldsymbol {e}}={\begin{pmatrix}0.001&0.001&0.002\\-0.001&0.002&0.002\\0.001&0.003&0.002\end{pmatrix}}}
We can break any tensor into a fully symmetric and fully anti-symmetric tensor resulting in an anti-symmetric rotation tensor
ω
=
(
0
e
12
−
e
21
2
e
13
−
e
31
2
e
21
−
e
12
2
0
e
23
−
e
32
2
e
31
−
e
13
2
e
32
−
e
23
2
0
)
=
(
0
0.001
0.0005
−
0.001
0
−
0.0005
−
0.0005
0.0005
0
)
{\displaystyle {\boldsymbol {\omega }}={\begin{pmatrix}0&{\frac {e_{12}-e_{21}}{2}}&{\frac {e_{13}-e_{31}}{2}}\\{\frac {e_{21}-e_{12}}{2}}&0&{\frac {e_{23}-e_{32}}{2}}\\{\frac {e_{31}-e_{13}}{2}}&{\frac {e_{32}-e_{23}}{2}}&0\end{pmatrix}}={\begin{pmatrix}0&0.001&0.0005\\-0.001&0&-0.0005\\-0.0005&0.0005&0\end{pmatrix}}}
and symmetric strain tensor
ε
=
(
e
11
e
12
+
e
21
2
e
13
+
e
31
2
e
21
+
e
12
2
e
22
e
23
+
e
32
2
e
31
+
e
13
2
e
32
+
e
23
2
e
33
)
=
(
0.001
0
0.0015
0
0
0.0025
0.0015
0.0025
0
)
{\displaystyle {\boldsymbol {\varepsilon }}={\begin{pmatrix}e_{11}&{\frac {e_{12}+e_{21}}{2}}&{\frac {e_{13}+e_{31}}{2}}\\{\frac {e_{21}+e_{12}}{2}}&e_{22}&{\frac {e_{23}+e_{32}}{2}}\\{\frac {e_{31}+e_{13}}{2}}&{\frac {e_{32}+e_{23}}{2}}&e_{33}\end{pmatrix}}={\begin{pmatrix}0.001&0&0.0015\\0&0&0.0025\\0.0015&0.0025&0\end{pmatrix}}}
resulting ultimately in
e
=
ω
+
ε
{\displaystyle {\boldsymbol {e}}={\boldsymbol {\omega }}+{\boldsymbol {\varepsilon }}}
Within linear, homogeneous, isotropic elasticity theory, for a given stress state (units in MPa) determine the strain state given the Poisson ratio is 0.40 and the shear modulus is 50 GPa. Identify the hydrostatic stress, deviatoric stresses, strain dilatation, and strain deviator.
σ
=
(
10
2
2
2
5
−
3
2
−
3
−
5
)
{\displaystyle {\boldsymbol {\sigma }}={\begin{pmatrix}10&2&2\\2&5&-3\\2&-3&-5\end{pmatrix}}}
We're given the stress, so returning a solution requires determining the strain, which can be determined by
ε
i
j
=
1
+
ν
E
σ
i
j
−
ν
E
σ
k
k
δ
i
j
{\displaystyle \varepsilon _{ij}={\frac {1+\nu }{E}}\sigma _{ij}-{\frac {\nu }{E}}\sigma _{kk}\delta _{ij}}
We're given the Poisson ratio,
ν
{\displaystyle \nu }
G
{\displaystyle G}
E
{\displaystyle E}
G
=
E
2
(
1
−
ν
)
{\displaystyle G={\frac {E}{2\left(1-\nu \right)}}}
which can be inverted to
E
=
2
G
(
1
−
ν
)
{\displaystyle E=2G\left(1-\nu \right)}
Upon substitution this yields
E
=
60
{\displaystyle E=60}
ε
=
(
1
+
ν
E
σ
11
−
ν
E
(
σ
22
+
σ
33
)
σ
12
2
G
σ
13
2
G
σ
21
2
G
1
+
ν
E
σ
22
−
ν
E
(
σ
11
+
σ
33
)
σ
23
2
G
σ
31
2
G
σ
32
2
G
1
+
ν
E
σ
33
−
ν
E
(
σ
11
+
σ
22
)
)
=
(
0.1667
0.0467
0.0467
0.0467
0.0500
−
0.0700
0.0467
−
0.0700
−
0.1833
)
.
{\displaystyle {\boldsymbol {\varepsilon }}={\begin{pmatrix}{\frac {1+\nu }{E}}\sigma _{11}-{\frac {\nu }{E}}\left(\sigma _{22}+\sigma _{33}\right)&{\frac {\sigma _{12}}{2G}}&{\frac {\sigma _{13}}{2G}}\\{\frac {\sigma _{21}}{2G}}&{\frac {1+\nu }{E}}\sigma _{22}-{\frac {\nu }{E}}\left(\sigma _{11}+\sigma _{33}\right)&{\frac {\sigma _{23}}{2G}}\\{\frac {\sigma _{31}}{2G}}&{\frac {\sigma _{32}}{2G}}&{\frac {1+\nu }{E}}\sigma _{33}-{\frac {\nu }{E}}\left(\sigma _{11}+\sigma _{22}\right)\end{pmatrix}}={\begin{pmatrix}0.1667&0.0467&0.0467\\0.0467&0.0500&-0.0700\\0.0467&-0.0700&-0.1833\end{pmatrix}}.}
The hydrostatic stress is
σ
m
=
σ
k
k
3
=
σ
11
+
σ
22
+
σ
33
3
=
10
+
5
−
5
3
=
3.33
GPa
{\displaystyle \sigma _{m}={\frac {\sigma _{kk}}{3}}={\frac {\sigma _{11}+\sigma _{22}+\sigma _{33}}{3}}={\frac {10+5-5}{3}}=3.33{\text{ GPa}}}
The strain dilatation is
Δ
=
(
1
+
ε
11
)
(
1
+
ε
22
)
(
1
+
ε
33
)
−
1
=
(
1
+
0.1667
)
(
1
+
0.0500
)
(
1
+
0.1833
)
−
1
=
0.4496
{\displaystyle \Delta =\left(1+\varepsilon _{11}\right)\left(1+\varepsilon _{22}\right)\left(1+\varepsilon _{33}\right)-1=\left(1+0.1667\right)\left(1+0.0500\right)\left(1+0.1833\right)-1=0.4496}
which results in a mean strain of
ε
m
=
Δ
3
=
0.4496
3
=
0.1499
{\displaystyle \varepsilon _{m}={\frac {\Delta }{3}}={\frac {0.4496}{3}}=0.1499}
(Note that when strain is small
Δ
≈
ε
11
+
ε
22
+
ε
33
=
0.400
{\displaystyle \Delta \approx \varepsilon _{11}+\varepsilon _{22}+\varepsilon _{33}=0.400}
ε
m
≈
0.1333
{\displaystyle \varepsilon _{m}\approx 0.1333}
σ
′
=
(
10
−
3.33
2
2
2
5
−
3.33
−
3
2
−
3
−
5
−
3.33
)
=
(
6.67
2
2
2
1.67
−
3
2
−
3
−
8.33
)
{\displaystyle {\boldsymbol {\sigma '}}={\begin{pmatrix}10-3.33&2&2\\2&5-3.33&-3\\2&-3&-5-3.33\end{pmatrix}}={\begin{pmatrix}6.67&2&2\\2&1.67&-3\\2&-3&-8.33\end{pmatrix}}}
and
ε
′
=
(
0.1667
−
0.1499
0.0467
0.0467
0.0467
0.0500
−
0.1499
−
0.0700
0.0467
−
0.0700
−
0.1833
−
0.1499
)
=
(
0.0168
0.0467
0.0467
0.0467
0.0999
−
0.0700
0.0467
−
0.0700
−
0.3332
)
{\displaystyle {\boldsymbol {\varepsilon '}}={\begin{pmatrix}0.1667-0.1499&0.0467&0.0467\\0.0467&0.0500-0.1499&-0.0700\\0.0467&-0.0700&-0.1833-0.1499\end{pmatrix}}={\begin{pmatrix}0.0168&0.0467&0.0467\\0.0467&0.0999&-0.0700\\0.0467&-0.0700&-0.3332\end{pmatrix}}}
Within linear, homogeneous, isotropic elasticity theory, for a given strain state determine the stress state given the bulk modulus of 100 GPa and Lam
e
´
{\displaystyle {\acute {e}}}
ε
=
(
0.002
0.002
0.001
0.002
0.002
0.001
0.001
0.001
−
0.001
)
{\displaystyle {\boldsymbol {\varepsilon }}={\begin{pmatrix}0.002&0.002&0.001\\0.002&0.002&0.001\\0.001&0.001&-0.001\end{pmatrix}}}
We are given the strain, so returning a solution requires determining the stress, which can be determined by
σ
i
j
=
E
1
+
ν
ε
i
j
−
ν
E
(
1
+
ν
)
(
1
−
2
ν
)
ε
k
k
δ
i
j
{\displaystyle \sigma _{ij}={\frac {E}{1+\nu }}\varepsilon _{ij}-{\frac {\nu E}{\left(1+\nu \right)\left(1-2\nu \right)}}\varepsilon _{kk}\delta _{ij}}
where
ν
E
(
1
+
ν
)
(
1
−
2
ν
)
{\displaystyle {\frac {\nu E}{\left(1+\nu \right)\left(1-2\nu \right)}}}
λ
{\displaystyle \lambda }
G
=
E
2
(
1
+
ν
)
{\displaystyle G={\frac {E}{2\left(1+\nu \right)}}}
and
G
=
3
(
K
−
λ
)
2
{\displaystyle G={\frac {3\left(K-\lambda \right)}{2}}}
we know
E
(
1
+
ν
)
=
3
(
K
−
λ
)
{\displaystyle {\frac {E}{\left(1+\nu \right)}}=3\left(K-\lambda \right)}
The stress expression becomes
σ
i
j
=
3
(
K
−
λ
)
ε
i
j
+
λ
ε
k
k
δ
i
j
{\displaystyle \sigma _{ij}=3\left(K-\lambda \right)\varepsilon _{ij}+\lambda \varepsilon _{kk}\delta _{ij}}
Substituting and solving yields
σ
=
(
0.45
0.3
0.15
0.3
0.45
0.15
0.15
0.15
0.0
)
{\displaystyle {\boldsymbol {\sigma }}={\begin{pmatrix}0.45&0.3&0.15\\0.3&0.45&0.15\\0.15&0.15&0.0\end{pmatrix}}}
The hydrostatic stress is
σ
m
=
σ
k
k
3
=
σ
11
+
σ
22
+
σ
33
3
=
0.45
+
0.45
+
0.0
3
=
0.30
GPa
{\displaystyle \sigma _{m}={\frac {\sigma _{kk}}{3}}={\frac {\sigma _{11}+\sigma _{22}+\sigma _{33}}{3}}={\frac {0.45+0.45+0.0}{3}}=0.30{\text{ GPa}}}
The strain dilatation is
Δ
=
(
1
+
ε
11
)
(
1
+
ε
22
)
(
1
+
ε
33
)
−
1
=
(
1
+
0.002
)
(
1
+
0.002
)
(
1
−
0.001
)
−
1
=
0.003
{\displaystyle \Delta =\left(1+\varepsilon _{11}\right)\left(1+\varepsilon _{22}\right)\left(1+\varepsilon _{33}\right)-1=\left(1+0.002\right)\left(1+0.002\right)\left(1-0.001\right)-1=0.003}
which results in a mean strain of
ε
m
=
Δ
3
=
0.003
3
=
0.001
{\displaystyle \varepsilon _{m}={\frac {\Delta }{3}}={\frac {0.003}{3}}=0.001}
An interesting observation is that the strain dilation and hydrostatic (mean) stress are related by the bulk modulus
σ
m
=
K
Δ
{\displaystyle \sigma _{m}=K\Delta }
0.3
=
100
×
0.003
{\displaystyle 0.3=100\times 0.003}
The deviatoric stress and strain are then determined by subtracting the mean stress and strain from their respective tensors diagonal.
σ
′
=
(
0.45
−
0.30
0.30
0.15
0.30
0.45
−
0.30
0.15
0.15
0.15
0.00
−
0.30
)
=
(
0.15
0.30
0.15
0.30
0.15
0.15
0.15
0.15
−
0.30
)
{\displaystyle {\boldsymbol {\sigma '}}={\begin{pmatrix}0.45-0.30&0.30&0.15\\0.30&0.45-0.30&0.15\\0.15&0.15&0.00-0.30\end{pmatrix}}={\begin{pmatrix}0.15&0.30&0.15\\0.30&0.15&0.15\\0.15&0.15&-0.30\end{pmatrix}}}
and
ε
′
=
(
0.002
−
0.001
0.002
0.001
0.002
0.002
−
0.001
0.001
0.001
0.001
−
0.001
−
0.001
)
=
(
0.001
0.002
0.001
0.002
0.001
0.001
0.001
0.001
−
0.002
)
{\displaystyle {\boldsymbol {\varepsilon '}}={\begin{pmatrix}0.002-0.001&0.002&0.001\\0.002&0.002-0.001&0.001\\0.001&0.001&-0.001-0.001\end{pmatrix}}={\begin{pmatrix}0.001&0.002&0.001\\0.002&0.001&0.001\\0.001&0.001&-0.002\end{pmatrix}}}
For a single crystal of cubic zirconia, which has a elastic constants approximately
c
11
=
575
{\displaystyle c_{11}=575}
c
12
=
115
{\displaystyle c_{12}=115}
c
44
=
75
{\displaystyle c_{44}=75}
[
100
]
{\displaystyle \left[100\right]}
[
110
]
{\displaystyle \left[110\right]}
200
G
P
a
{\displaystyle 200\ GPa}
0.3
{\displaystyle 0.3}
Say that the
[
100
]
{\displaystyle \left[100\right]}
x
1
{\displaystyle x_{1}}
U
o
{\displaystyle U_{o}}
U
o
=
1
2
σ
i
j
ε
i
j
{\displaystyle U_{o}={\frac {1}{2}}\sigma _{ij}\varepsilon _{ij}}
so
d
U
o
=
1
2
σ
i
j
d
ε
i
j
{\displaystyle dU_{o}={\frac {1}{2}}\sigma _{ij}d\varepsilon _{ij}}
In the case of anisotropic elasticity theory
σ
i
j
=
c
i
j
k
l
ε
k
l
.
{\displaystyle \sigma _{ij}=c_{ijkl}\varepsilon _{kl}.}
In this case all
ε
i
j
=
0
{\displaystyle \varepsilon _{ij}=0}
ε
11
=
0.001
{\displaystyle \varepsilon _{11}=0.001}
σ
i
j
=
0
{\displaystyle \sigma _{ij}=0}
σ
11
=
c
1111
ε
11
{\displaystyle \sigma _{11}=c_{1111}\varepsilon _{11}}
σ
22
=
c
1122
ε
22
{\displaystyle \sigma _{22}=c_{1122}\varepsilon _{22}}
σ
33
=
c
1122
ε
33
{\displaystyle \sigma _{33}=c_{1122}\varepsilon _{33}}
Substituting into the above equationsː
d
U
0
=
ε
11
c
1111
d
ε
11
+
ε
11
c
1122
d
ε
22
+
ε
11
c
1122
d
ε
33
⏟
=
0
u
p
o
n
i
n
t
e
g
r
a
t
i
o
n
=
ε
11
c
1111
d
ε
11
U
0
=
∫
0
ε
11
=
0.001
ε
11
c
11
d
ε
11
=
c
11
ε
11
2
2
|
0
0.001
=
(
575
∗
10
9
P
a
)
0.001
2
2
=
288
k
J
{\displaystyle {\begin{aligned}dU_{0}&=\varepsilon _{11}c_{1111}d\varepsilon _{11}+\underbrace {\varepsilon _{11}c_{1122}\ d\varepsilon _{22}+\varepsilon _{11}c_{1122}\ d\varepsilon _{33}} _{=\ 0\ upon\ integration}\\&=\varepsilon _{11}c_{1111}d\varepsilon _{11}\\\\U_{0}&=\int _{0}^{\varepsilon _{11}\ =\ 0.001}\varepsilon _{11}c_{11}d\varepsilon _{11}\\&=\left.c_{11}{\varepsilon _{11}^{2} \over 2}\ \right|_{0}^{0.001}\\&=(575*10^{9}\ Pa){0.001^{2} \over 2}\\&=288\ kJ\end{aligned}}}
For a single crystal of cubic zirconia, which has a elastic constants approximately
c
11
=
575
{\displaystyle c_{11}=575}
c
12
=
115
{\displaystyle c_{12}=115}
c
44
=
75
{\displaystyle c_{44}=75}
[
100
]
{\displaystyle \left[100\right]}
(
001
)
{\displaystyle \left(001\right)}
[
010
]
{\displaystyle \left[010\right]}
Obeying the given order of operation, first we apply a uniaxial load of
0.001
{\displaystyle 0.001}
[
100
]
{\displaystyle [100]}
Note that our general equations are
d
U
=
σ
i
j
d
ε
i
j
{\textstyle dU=\sigma _{ij}\ d\varepsilon _{ij}}
σ
i
j
=
c
i
j
k
l
ε
k
l
{\textstyle \sigma _{ij}=c_{ijkl}\varepsilon _{kl}}
Restating the strain tensorː
ε
=
(
ε
11
0
0
0
0
0
0
0
0
)
{\displaystyle \varepsilon =\left({\begin{matrix}\varepsilon _{11}&0&0\\0&0&0\\0&0&0\end{matrix}}\right)}
From this we get the non-zero stress tensorː
σ
=
(
ε
11
c
11
0
0
0
ε
11
c
12
0
0
0
ε
11
c
12
)
{\displaystyle \sigma =\left({\begin{matrix}\varepsilon _{11}c_{11}&0&0\\0&\varepsilon _{11}c_{12}&0\\0&0&\varepsilon _{11}c_{12}\end{matrix}}\right)}
Thus the only non-zero
d
ε
i
j
{\displaystyle d\varepsilon _{ij}}
d
ε
11
{\displaystyle d\varepsilon _{11}}
d
U
{\textstyle dU}
U
1
=
288
k
J
{\displaystyle U_{1}=288\ kJ}
Now let's apply the shear
0.001
{\displaystyle 0.001}
(
100
)
{\displaystyle (100)}
[
010
]
{\displaystyle [010]}
Our new stress tensor isː
σ
=
(
ε
11
c
11
ε
12
c
44
0
ε
12
c
44
ε
11
c
12
0
0
0
ε
11
c
12
)
{\displaystyle \sigma =\left({\begin{matrix}\varepsilon _{11}c_{11}&\varepsilon _{12}c_{44}&0\\\varepsilon _{12}c_{44}&\varepsilon _{11}c_{12}&0\\0&0&\varepsilon _{11}c_{12}\end{matrix}}\right)}
Here, the only non-zero terms are
d
ε
12
{\displaystyle d\varepsilon _{12}}
d
ε
21
{\displaystyle d\varepsilon _{21}}
Once again utilizing our basic energy equation we getː
d
U
=
σ
i
j
d
ε
i
j
=
ε
12
c
44
d
ε
12
U
2
=
2
∫
0
ε
12
ε
12
c
44
d
ε
12
=
2
[
c
44
ε
12
2
2
]
0
ε
12
=
(
75
∗
10
9
P
a
)
0.001
2
U
2
=
75
k
J
{\displaystyle {\begin{aligned}dU&=\sigma _{ij}\ d\varepsilon _{ij}=\varepsilon _{12}c_{44}\ d\varepsilon _{12}\\\\U_{2}&=2\int _{0}^{\varepsilon _{12}}\varepsilon _{12}c_{44}\ d\varepsilon _{12}\\&=2\left[c_{44}{\varepsilon _{12}^{2} \over 2}\right]_{0}^{\varepsilon _{12}}\\&=(75*10^{9}\ Pa)0.001^{2}\\U_{2}&=75\ kJ\end{aligned}}}
Finally, adding
U
1
{\displaystyle U_{1}}
U
2
{\displaystyle U_{2}}
363
k
J
{\displaystyle 363\ kJ}
For a polycrystal specimen of cubic zirconia, which has a elastic constants approximately
c
11
=
575
{\displaystyle c_{11}=575}
c
12
=
115
{\displaystyle c_{12}=115}
c
44
=
75
{\displaystyle c_{44}=75}
200
G
P
a
{\displaystyle 200\ GPa}
0.3
{\displaystyle 0.3}
ε
=
(
0.001
0.001
0.000
0.001
0.000
0.000
0.000
0.000
0.000
)
{\displaystyle {\boldsymbol {\varepsilon }}={\begin{pmatrix}0.001&0.001&0.000\\0.001&0.000&0.000\\0.000&0.000&0.000\end{pmatrix}}}
If the polycrystal material has a porosity of 2% approximately how much will this change the elastic modulus? Approximately how much will this change the elastic energy for this applied strain?
Note that our general equations are
d
U
=
σ
i
j
d
ε
i
j
{\textstyle dU=\sigma _{ij}\ d\varepsilon _{ij}}
σ
i
j
=
c
i
j
k
l
ε
k
l
{\textstyle \sigma _{ij}=c_{ijkl}\varepsilon _{kl}}
Here, we can put the stress in terms of the elastic modulus and the Poisson's ratioː
σ
i
j
=
E
1
+
ν
ε
i
j
+
ν
E
(
1
+
ν
)
(
1
−
2
ν
)
ε
k
k
∂
i
j
{\displaystyle \sigma _{ij}={E \over 1+\nu }\varepsilon _{ij}+{\nu E \over (1+\nu )(1-2\nu )}\varepsilon _{kk}\partial _{ij}}
Where the latter constant is equivalent to the Lamé Constant (
λ
{\displaystyle \lambda }
λ
=
ν
E
(
1
+
ν
)
(
1
−
2
ν
)
{\displaystyle \lambda ={\nu E \over (1+\nu )(1-2\nu )}}
Briefly solving for the Lamé Constant yields usː
λ
=
ν
E
(
1
+
ν
)
(
1
−
2
ν
)
=
0.3
∗
200
G
P
a
(
1
+
0.3
)
(
1
−
2
(
0.3
)
)
=
115.3846
G
P
a
{\displaystyle {\begin{aligned}\lambda &={\nu E \over (1+\nu )(1-2\nu )}\\&={0.3*200\ GPa \over (1+0.3)(1-2(0.3))}=115.3846\ GPa\end{aligned}}}
Keeping in mind that
ε
12
{\displaystyle \varepsilon _{12}}
ε
21
{\displaystyle \varepsilon _{21}}
σ
=
(
E
1
+
ν
ε
11
+
λ
ε
11
E
1
+
ν
ε
12
0
E
1
+
ν
ε
12
λ
ε
11
0
0
0
λ
ε
11
)
{\displaystyle \sigma =\left({\begin{matrix}{E \over 1+\nu }\varepsilon _{11}+\lambda \varepsilon _{11}&{E \over 1+\nu }\varepsilon _{12}&0\\{E \over 1+\nu }\varepsilon _{12}&\lambda \varepsilon _{11}&0\\0&0&\lambda \varepsilon _{11}\end{matrix}}\right)}
Therefore, we can write out the non-zero energy terms asː
d
U
=
σ
i
j
d
ε
i
j
=
(
E
1
+
ν
+
λ
)
ε
11
d
ε
11
+
(
E
1
+
ν
+
λ
)
ε
12
d
ε
12
+
(
E
1
+
ν
+
λ
)
ε
21
d
ε
21
+
λ
ε
11
d
ε
11
+
λ
ε
11
d
ε
11
=
(
E
1
+
ν
+
λ
)
ε
11
d
ε
11
+
2
(
E
1
+
ν
+
λ
)
ε
12
d
ε
12
U
=
(
E
1
+
ν
+
λ
)
1
2
ε
11
2
|
0
ε
11
+
(
E
1
+
ν
)
ε
12
2
|
0
ε
12
=
288
k
J
{\displaystyle {\begin{aligned}dU&=\sigma _{ij}\ d\varepsilon _{ij}\\&=\left({E \over 1+\nu }+\lambda \right)\varepsilon _{11}\operatorname {d} \!\varepsilon _{11}+\left({E \over 1+\nu }+\lambda \right)\varepsilon _{12}\operatorname {d} \!\varepsilon _{12}+\left({E \over 1+\nu }+\lambda \right)\varepsilon _{21}\operatorname {d} \!\varepsilon _{21}+\lambda \varepsilon _{11}\operatorname {d} \varepsilon _{11}+\lambda \varepsilon _{11}\operatorname {d} \varepsilon _{11}\\&=\left({E \over 1+\nu }+\lambda \right)\varepsilon _{11}\operatorname {d} \!\varepsilon _{11}+2\left({E \over 1+\nu }+\lambda \right)\varepsilon _{12}\operatorname {d} \!\varepsilon _{12}\\\\U&=\left.\left({E \over 1+\nu }+\lambda \right){1 \over 2}\varepsilon _{11}^{2}\right|_{0}^{\varepsilon _{11}}+\left.\left({E \over 1+\nu }\right)\varepsilon _{12}^{2}\right|_{0}^{\varepsilon _{12}}\\&=288\ kJ\end{aligned}}}




















































































































![{\displaystyle \left[100\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd21195ca6ec3a305a0f96b58aa56d725175e550)
![{\displaystyle \left[110\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec690830a124ff30d8cdeef434cfd8730e3fbfcb)














![{\displaystyle \left[010\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f638112e2a70d4eea1ef1901e85ee3886e642c8)

![{\displaystyle [100]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f136cc39fc2e358ec08d93e4e7a0e2c108c9538a)









![{\displaystyle [010]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11eb1613d9138c5fc420b5cfdae5b74575a26e9e)



![{\displaystyle {\begin{aligned}dU&=\sigma _{ij}\ d\varepsilon _{ij}=\varepsilon _{12}c_{44}\ d\varepsilon _{12}\\\\U_{2}&=2\int _{0}^{\varepsilon _{12}}\varepsilon _{12}c_{44}\ d\varepsilon _{12}\\&=2\left[c_{44}{\varepsilon _{12}^{2} \over 2}\right]_{0}^{\varepsilon _{12}}\\&=(75*10^{9}\ Pa)0.001^{2}\\U_{2}&=75\ kJ\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cff27ede42afcb17c48415cfafa804bc1ff5704)










