Origami/Techniques/Practice
Most origami folds can be broken down into simpler steps.
Basic skills
[edit | edit source]Valley fold
[edit | edit source]
A valley fold is the first basic fold, in which the paper is folded in front of itself. The valley fold — which most people do as "just fold the paper in half" — is really made of substeps. These steps help fold the paper very precisely, which is important in complicated models. Here is one way to make the valley fold very precisely:
- Pull the bottom edge up and forward.
- Loosely fold, without making a crease.
- Line up edges.
- Line up a corner (by lining up the edges on one side, and lining up the edges on the other side).
- Hold (a loosely folded, uncreased) paper down to prevent slipping.
- While holding the paper down so it does not slip, spread out a flat area on the paper. This is often done by holding the paper down at two edges with your index fingers. Also hold down the paper with one (or both) thumbs. Gradually move your thumb(s) away from your finger(s), pushing your thumb into the paper, but pulling the paper taut between your thumb(s) and your fingers.
- Pinch a crease. While holding the paper down so it does not slip, spread your thumb(s) far enough from the edge that they reach the intended crease line.
- Resolve the crease. Without letting up on the paper, continue the spreading motion until the crease is sharp. The crease should be exactly where you intended it to be, without any waviness in the edge, without any "bubbles" in the layers of paper, and without any slipping of the paper at the edge(s) or corner(s).
Mountain fold
[edit | edit source]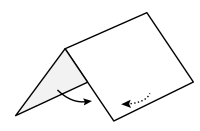
A mountain fold is much the same as a valley fold, except in one respect: it is in the opposite direction. This can present problems with the folding order, as valley folds are occasionally performed when there are other layers of paper underneath and the paper cannot merely be turned over. Therefore, to complete a mountain fold, these instructions must be followed:
Summary: fold the paper behind itself
- Lightly pinch the paper along where the crease will be.
- Pull the bottom of flap to be folded behind itself, but without trapping other layers of paper between them (this is only a problem if there are flaps behind the section to be folded, and can be avoided if the flaps are pulled apart a bit to open them and give you more space to fold)
- Line up the pinch marks with the edges of the paper.
- While holding the paper down so it does not slip, spread out a flat area on the paper. This is often done by holding the paper down at two edges with your index fingers. Also hold down the paper with one (or both) thumbs. Gradually move your thumb(s) away from your finger(s), pushing your thumb into the paper, but pulling the paper taut between your thumb(s) and your fingers.
- Pinch a crease. While holding the paper down so it does not slip, spread your thumb(s) far enough from the edge that they reach the intended crease line.
- Resolve the crease. Without letting up on the paper, continue the spreading motion until the crease is sharp. The crease should be exactly where you intended it to be, without any waviness in the edge, without any "bubbles" in the layers of paper, and without any slipping of the paper at the edge(s) or corner(s).
Simple compound folds
[edit | edit source]Simple compound folds require simultaneous valley and mountain folds but the creases can be made before the actual folding.
Inside reverse fold
[edit | edit source]
An inside reverse fold consists of two radial mountain folds extending from a single point on a central fold, and a reversal of the central fold on the affected end, all done simultaneously. Here is one way to do the inside reverse fold:
- Start with a flap. Decide where you want to make the inside reverse fold.
- Valley fold the paper along the chosen line.
- Unfold to step 2.
- Separate the two hidden layers of paper, so that you are half-way between step 1 and step 2. You will see the vee-shaped pair of creases formed in step 2.
- Push the tip of the paper into the gap you just made.
- One of the creases (of the vee) will already be in the correct direction (a valley fold as seen from inside; a mountain fold as seen from outside). The other crease will be in the opposite direction. Reverse the second crease, so that both creases are valley folds as seen from the inside, and [mountain fold]s as seen from the outside.
- Reverse the lower left edge, so that it is a mountain fold as seen from the inside, and a valley fold as seen from the outside.
- "Pop" all three creases into place.
- Close up the model again.
- The inside reverse fold is done. (Notice how you reversed the folds to put the tip inside the model--thus the name.)
Outside reverse fold
[edit | edit source]
An outside reverse fold consists of two radial valley folds extending from a single point on a central fold and a reversal of the center fold on the affected end, all done simultaneously.
Low-intermediate skills
[edit | edit source]Low-intermediate skills require simultaneous valley and mountain folds but not all the creases can be made before the actual folding.
Squash fold
[edit | edit source]
The squash fold starts with a flap with at least two layers.
- Make a radial fold from the closed point down the center of this flap.
- Open the flap and refold downward to make two adjacent flaps.
Rabbit ear fold
[edit | edit source]A rabbit ear fold starts with a reference crease down a diagonal. Fold two radial folds from opposite corners along the same side of the reference crease; the resulting flap should be folded downwards so that the previous edges are aligned.

Petal fold
[edit | edit source]A petal fold starts with two connected flaps, each of which has at least two layers. The two flaps are attached to each other along a reference crease. Make two radial folds from the open point, so that the open edges lie along the reference crease. Unfold these two radial folds. Make another fold across the top connecting the ends of the creases to create a triangle of creases. Unfold this fold as well. Fold one layer of the open point upward and flatten it using the existing creases. A petal fold is equivalent to two side-by-side rabbit ears, which are connected along the reference crease.
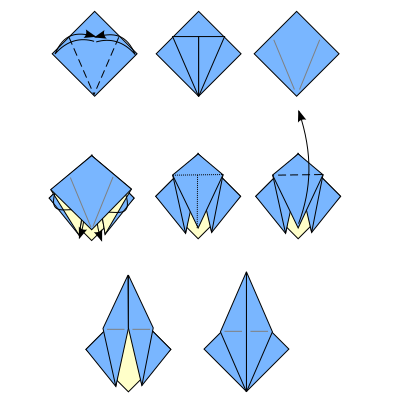
Mid-intermediate skills
[edit | edit source]Swivel fold
[edit | edit source]
The swivel fold is difficult to describe as the term is loosely defined and there are so many different versions that could be called "swivel folds". However, generally swivel folds consists of swivelling a flap of paper at a certain point or vertex in order that the raised edge of the flap will lie on the edge of the flap that doesn't move:
- You should start with a sheet that is already fold,
- Take the corner of an overflowed paper and make a fold that cut the corner in the middle; doing so, one edge of the corner will lie on the other edge of the corner,
- Make a radial fold which starts from the same point of the previous fold; you can choose the angle of this fold; it depends on the origami you want to make,
- Open the flap,
- Refold downward,
- Make the edge of the flap lying on the other edge.
Pentagon
[edit | edit source]Although most origami models start with a square or rectangular sheet of paper, a few start with a triangle, pentagon, hexagon, circle, or other convex sheet of paper. A pentagon can be traced (from a template) onto a square sheet of paper, or it can be folded from a square sheet of paper. One technique for folding a pentagon uses folds to calculate the golden ratio: (1+sqrt(5))/2. Another technique for folding a pentagon uses folds to divide a 180 degree angle into five (almost exactly) equal angles. The excess paper is often trimmed, before starting to fold the desired model. Pentagons are used in five-sided flowers, such as the cherry blossom and Marie's Rose.
High-intermediate skills
[edit | edit source]Spread squash
[edit | edit source]The spread squash can similarly be considered the sinked analog of the squash fold. It is used to flatten a closed flap or twist fold (see below). Instead of creating a long point to one side of the flap's base, the spread squash creates a wide splat around the flap's base. The spread squash is used in the eyes of Engel's Octopus, in Marie's Rose, and in some other intermediate and complex models.
Open sink
[edit | edit source]
The open sink usually involves opening out the paper, and reversing creases to make a waterbomb base in the middle of the model.
Open double sink
[edit | edit source]The open double sink is equivalent to making an open sink, and then open-sinking the point in the opposite direction. It is a sinked analog of the crimp fold. When made in a single step (after pre-creasing), it can be easier to make than a single open sink, because it does not require neatly reversing the point. The open double sink is used in many box-pleated models.
Closed sink
[edit | edit source]The closed sink simultaneously makes a locking flap inside of a sink. It is difficult because the paper cannot be opened out further than a triangle. This technique is illustrated in the Origami Forum's thread #462. The closed sink appears in some high-intermediate and complex models.
Twist fold
[edit | edit source]
The twist fold involves, as the name implies, twisting a section of the paper with respect to its original position. The section twisted will be a polygon; the numerous required support creases include pleat folds radiating from its corners. Marie's Rose demonstrates this on a pentagon.
It is also possible to twist a single conical point indefinitely, collapsing the sides in a waterbomb-base-like fashion as one goes. (If this is tried with a non-conical point, such as the waterbomb base itself, eventually the fold will terminate in a spread squash.) This variant is used in many of Tomoko Fuse's modular boxes.
Complex skills
[edit | edit source]Unsink
[edit | edit source]The unsink, or sometimes open unsink, makes a concave pocket convex without fully unfolding the paper, or the opposite of an open sink. It is more difficult than the closed unsink below because there is no internal flap to grab onto to help unsink the paper, so the paper must be opened out and the area to be unsunk is pushed out (to be convex) from inside the model and from behind. It is a common fold in Lang's insects.
Closed unsink
[edit | edit source]The closed unsink inverts a closed sink without completely opening out the affected paper. In theory, it is "just" the opposite of a closed sink. In practice, it is very difficult, because the paper being "popped" into place usually must be pulled (not pushed), and because it involves simultaneously folding over a locking flap that is hidden inside the sink. However, it is easier to manipulate than an open unsink as there is an internal flap to pull to pop the unsink in place; in an open unsink there is nothing to hold. The closed unsink appears in some complex models, such as a few of Lang's insects.