OPT Design

Tube Output Transformer Design
[edit | edit source]The goal of this book is to show the world how an output transformer or OPT may be designed and what to think of.
Theory
[edit | edit source]The fundamental consideration is that the core must not go into saturation at any voltage or frequency. That means that the core must widthstand:
Due to DC almost always being present (especially true in single-end designs) we must also consider the magnetic intensity H:
where lm is the mean magnetic length around the core.
It can furthermore be shown that the primary inductance need emerges from the fact that
where RL is the reflected load resistance and rp is the plate resistance of the tube(s).
This yields the equation
where ZL is the loudspeaker nominal impedance and n the turn-ratio of the transformer.
It can furthermore be shown that maximum output power occurs when each tube is loaded by
Knowing this the minimum inductance L may be calculated.
The small signal model do however also put restrictions on HF parameters. If the OPT is carefully wound (in sectors and not bifilaryTemplate:Fix/category[check spelling] as well as at least one layer of transformer tape inbetween each layer) the main HF problem will be a so called leakage inductance. The equation for calculating this is:
or
This parameter is however very hard to control. But experience has showed that one important thing is that the secondary winding must cover the whole (or both) primaries. Another idea is that the winding ends must not be folded. This last part might mainly eliminate HF resonances.
The inductance of a toroidal transformer can be expressed as:
where
where lg is the length of the air-gap and lm is the mean magnetic length.
If lg is zero, this simplifies to
where
is the relative permeability of the iron and
is the permeability of vacuum.
A Practical Example
[edit | edit source]It can be shown that a single-pole low-pass filter roll-off yields an only -0,5dB impact on the frequency three times lower than fh. This means that if we want -0,5dB at highest audible frequency (20kHz) we would need a fh of 60kHz.
Because
this means a leakage inductance of less than
if we want to use KT66 tubes in push-pull (PP) where rp=2rp(KT66)=2500 Ohm. Observe that RL in PP-designs is 4 times the load on each tube. Optimum plat-to-plate load is thus 10k Ohms in our case.
The same thing is valid for single-pole high-pass filters, thus fl for -0.5dB@10Hz is 3,3Hz. The inductance therefor needs to be greater than
If we want to use the suggested core dimensions we get
and
Because P1+P2 needs to widthstand 230V@15Hz and a common maximum flux density for transformer irons is around
the number of turns can now be calculated using the first equation. This gives
Putting this into the equation for the primary inductance we get
Because we want to use the OPT in Class A push-pull configuration we need not take too much consideration of the DC that will flow due to tube aging and loudspeaker impedance variation with frequency. But it is recommended that the OPT should widthstand at least 10mADC thru both primaries. In SE-configuration a so called air-gap would be needed but this cannot (easily) be realised in toroidal transformers which makes us dependent on the width of the BH-loop of the used iron.
The magnetic intensity for a DC current of 10mA is for our transformer:
and here we want to have at least L/3=30H left.
Equation Derivation
[edit | edit source]In this paragraph the derivation of the above used equations will be explained.
Standard OPT Usage
[edit | edit source]
This picture shows how an OPT is used in push-pull (PP) configuration. The below theory is however also valid for single-end (SE) configurations.
OPT Small Signal Model
[edit | edit source]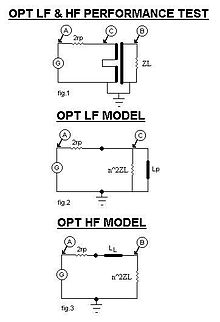
This picture shows the small signal model of the OPT.
Fig.1 shows the trivial OPT connection i.e driven by the generator G thru two plate resistances rp (because of PP).
Fig.2 shows what happens at low frequencies where the OPT works as an ordinary transformer. Reflected impedance is therefor
where n is the turn ratio of the OPT and ZL is the loudspeaker impedence.
Fig.3 shows what happens at high frequencies where the leakage inductance LL is dominant over the interlayer capacitance (due to special winding techniques described earlier). The above expression still holds though.
Transformer Basics
[edit | edit source]Consider an ideal transformer without iron or copper losses. The output power will then be equal to the input power.
If you transform a high voltage to a low voltage you will be then able to extract a higher current at the secondary than you are putting in on the primary.
So if
then
and if
it follows that
and finally
or
Small Signal Model Evaluation
[edit | edit source]While using Norton and Thevenin circuit theory in Fig.2 we get:
In Fig.3 we may however just realize the fact that
because this is where the reactance of LL becomes dominant.
Standard Filter Characteristics
[edit | edit source]Imagine a single-pole High-Pass filter. Then you might have a capacitor in series with a resistor to ground. The Laplace transfer function then yields
or simplified
Putting
we get
Putting s=jw we get
and the amplitude of the transfer function gets
or
where f is the frequency.
Putting
we get
Field Magnetics
[edit | edit source]In this paragraph we will show the world the electromagnetic fundamentals.
Maxwell's Equations
[edit | edit source]The normal form of Maxwell's Equations is
The first equation, Gauss's Law, describes how electrical fields are caused by electrical charges.
The second equation states that there are no "magnetic charges", or so called magnetic monopoles.
The third equation, Faraday's Law, describes how electrical fields are created due to magnetic field variations.
The fourth equation, Ampere's Law (with Maxwell's correction), describes how magnetic fields are created from electrical field variations.
A List of the Used Quanteties
[edit | edit source]E : Electric Field Intensity [V/m]
D : Electric Flux Density [As/m^2]
H : Magnetic Field Intensity [A/m]
B : Magnetic Flux Density [Vs/m^2]
Jf : Free Current Density [A/m^2]
Integral Form
[edit | edit source]
Boundary Limits
[edit | edit source]Going from medium 1 to medium 2 Maxwell's Equations gives
where
is the surface charge density och Kf the free surface current intensity between the mediums.
Faraday's Law
[edit | edit source]Consider Faraday's Law where we have from Maxwell's Equations:
If we define:
=emf induced in the curvature C [Volt]
and
=magnetic flux thru the surface S [Vs or Weber]
then we get:
[Volt]
If we use several turns N of wire we get
[Volt]
And if the magnetic flux flows thru an iron where
the magnetic flux will stay in the iron only, yielding a secondary voltage proportional to the turn ratio n.
Magnetic Flux Density in an Iron Core
[edit | edit source]From Faraday's Law we have
And due to no variations in the surface S, we have
Using the equation
we then get
A sinusoidal magnetic flux density yields
and thus
which maximum occurs when
Thus
or
where A has been substituted for S
And if the voltage is sinusoidal
we get
Magnetic Field Intensity in an Iron Core
[edit | edit source]From Maxwell's Equations we get
because we are considering DC only and a homogenous surface.
So if we are using a toroid, then
and if
then
Effective Permeability due to Air-Gap
[edit | edit source]Applying Ampere's law we once again get
Here we also have
But in the core we will have
and in the air-gap
This gives
This may be rewritten as
or
where
which gives
or
Toroidal Core Inductance
[edit | edit source]Consider cylindrical coordinates. Then we get
Since the path encircles a total current NI, we have
Knowing the relationship
it is easy to relate to the earlier equations, thus
and
which equals
Using that the flux linkage is
and that the small signal inductance is independent of the current, we get
C-Core Inductance
[edit | edit source]This is not so easy to calculate but we can do some approximations if the mean magnetic length could be defined by
where c is the shortest leg (at the center of the iron) and d the longest dito leg.
Approximating this to a circular toroidal shape, we get
Adding half of the thickness of the iron to this we get b, substracting half of the thickness we get a. Then we might reuse
This should be quite valid due to the magnetic flux staying in the iron because of
Optimizing Tube Amp Load
[edit | edit source]
If we consider
and realize that
output power may be written
and derivated by Ia this gives
with maxima for
thus
From the image we can see that
where Ua disappears so that
or
thus
A more simple way to prove this is by inspection of image:
This finally proves that optimum load for a triode is double it's internal resistance. It should however be pointed out that plate voltage should be the limiting factor, for higher voltages where plate dissipation comes into the picture, Ra must be higher.
It is also interesting to note that the efficiency is only 25% in this case, we can prove this by putting:
with
thus

![{\displaystyle B={\frac {U_{rms}}{4,44NAf}}[T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80bd1b305000cf821a76e13e2abca302fd763ea8)
![{\displaystyle H={\frac {NI}{lm}}[A/m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6793e69c9e965086fc58cd2d00e44f05a9f47ea)





![{\displaystyle L={\frac {\mu _{eff}N^{2}h}{2\pi }}\ln {\frac {b}{a}}[H]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c672290ae1d4dec4f0923f1920f2852d9d3e7e54)







![{\displaystyle A=6,25\cdot 10^{-4}[m^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/684a0dc9e097c59f6c41f95b70a79c9a52457617)
![{\displaystyle l_{m}=0,196[m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1ab800f98ae07b9b66f05284ce1d6664d28025a)


![{\displaystyle L=0,041\mu _{r}[H]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0464db0ceae9bfbd50160c236f34dfa65891d19)
![{\displaystyle H=176[A/m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75366e3a884c05313dea73d367b6170b3c583f8c)
























































































