OCR A-Level Physics/Fields, Particles and Frontiers of Physics/Electromagnetic Induction
In order to understand electromagnetic induction, it is necessary to appreciate what is meant by the magnetic flux linkage of a coil. Flux linkage can be calculated by magnetic flux * number of turns on coil, and, according to Faraday's law of electromagnetic induction, a changing flux linkage results in the induction of an e.m.f. across the coil equal in magnitude to the rate of change of flux linkage.
Faraday's and Lenz's Law
[edit | edit source]Faraday's
[edit | edit source]While Faraday's law gives the magnitude of the e.m.f., it is important to remember that e.m.f. is a vector.
induced e.m.f rate of change of flux linkage.
Lenz's
[edit | edit source]Consequently, it is also important to know the direction, something that can be calculated using Lenzs' law. This says that the direction of the induced e.m.f. will be such as to produce a magnetic field in the direction that resists the change in magnetic flux. For example, if magnetic flux is decreasing, an e.m.f. will be induced in the direction that leads to it increasing.
One Equation
[edit | edit source]Brought together, these two laws can be represented in a simple equation:
induced e.m.f. = - rate of change of flux linkage.
Lenz's Law is the negative part of this equation. The rest is Faraday's.
As we know flux linkage, , is the magnetic flux, multiplied by the number of turns,
Now we know all this we can deduce the following:
AC Generator
[edit | edit source]AC generators apply the above principles in order to generate electricity. In these generators, a coil of wire is rotated inside a magnetic field, changing the angle between the magnetic field and the coil and so changing magnetic flux. According to Faraday's law, this change will lead to the induction of an alternating e.m.f.
Transformers
[edit | edit source]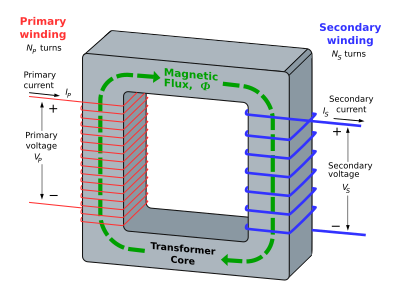
Transformers use the principles of electromagnetic induction to either increase (in step-up transformers) or decrease (in step-down transformers) the voltage. Its key use is in electricity transmission, where the voltage is increased significantly before being transmitted into a power line. This reduces the current (as P=VI and power is constant) and so increases the efficiency of this transmission process.
Transformers are made of two coils of wire, the primary (input) and the secondary (output) coil, wrapped around an iron core. The voltage across the two coils is shown by:
Vs = Voltage across secondary coil; Vp = Voltage across primary coil; ns = Number of turns on secondary coil; np = Number of turns on primary coil
We got to this equation by rearranging Faraday's law.
We then use 'n' rather than 'N' and we know that this relationship must be constant so we equate the primary and secondary together.
Transformers work by the following process:
- An alternating current is passed through the primary coil
- The alternating current in the primary coil leads the primary coil to produce a magnetic field of alternating direction (as the direction of the magnetic field and of the current are related by Fleming's left hand rule)
- The iron core ensures that the magnetic field is significantly stronger inside this core. This ensures that the as much of the changing magnetic flux produced by the primary coil as possible links the secondary coil.
- The changing magnetic flux in the secondary coil induces an e.m.f. across its ends.










