Linear Algebra/Topic: Analyzing Networks/Solutions

Solutions

Many of the systems for these problems are mostly easily solved on a computer.

Problem 1

Calculate the amperages in each part of each network.

1. This is a simple network.

   

2. Compare this one with the parallel case discussed above.

   

3. This is a reasonably complicated network.

   

Answer

1. The total resistance is $7$ ohms. With a $9$ volt potential, the flow will be $9/7$ amperes. Incidentally, the voltage drops will then be: $27/7$ volts across the $3$ ohm resistor, and $18/7$ volts across each of the two $2$ ohm resistors.
2. One way to do this network is to note that the $2$ ohm resistor on the left has a voltage drop across it of $9$ volts (and hence the flow through it is $9/2$ amperes), and the remaining portion on the right also has a voltage drop of $9$ volts, and so is analyzed as in the prior item. We can also use linear systems.

   

   Using the variables from the diagram we get a linear system

   ${\begin{array}{*{4}{rc}r}i_{0}&-&i_{1}&-&i_{2}&&&=&0\\&&i_{1}&+&i_{2}&-&i_{3}&=&0\\&&2i_{1}&&&&&=&9\\&&&&7i_{2}&&&=&9\end{array}}$

   which yields the unique solution $i_{1}=81/14$, $i_{1}=9/2$, $i_{2}=9/7$, and $i_{3}=81/14$.

   Of course, the first and second paragraphs yield the same answer. Essentially, in the first paragraph we solved the linear system by a method less systematic than Gauss' method, solving for some of the variables and then substituting.

3. Using these variables

   

   one linear system that suffices to yield a unique solution is this.

   ${\begin{array}{*{7}{rc}r}i_{0}&-&i_{1}&-&i_{2}&&&&&&&&&=&0\\&&&&i_{2}&-&i_{3}&-&i_{4}&&&&&=&0\\&&&&&&i_{3}&+&i_{4}&-&i_{5}&&&=&0\\&&i_{1}&&&&&&&+&i_{5}&-&i_{6}&=&0\\&&3i_{1}&&&&&&&&&&&=&9\\&&&&3i_{2}&&&+&2i_{4}&+&2i_{5}&&&=&9\\&&&&3i_{2}&+&9i_{3}&&&+&2i_{5}&&&=&9\end{array}}$

   (The last three equations come from the circuit involving $i_{0}$-$i_{1}$-$i_{6}$, the circuit involving $i_{0}$-$i_{2}$-$i_{4}$-$i_{5}$-$i_{6}$, and the circuit with $i_{0}$-$i_{2}$-$i_{3}$-$i_{5}$-$i_{6}$.) Octave gives $i_{0}=4.39437$, $i_{1}=3.00000$, $i_{2}=1.39437$, $i_{3}=0.38028$, $i_{4}=1.01408$, $i_{5}=1.39437$, $i_{6}=4.39437$.

Problem 2

In the first network that we analyzed, with the three resistors in series, we just added to get that they acted together like a single resistor of $10$ ohms. We can do a similar thing for parallel circuits. In the second circuit analyzed,

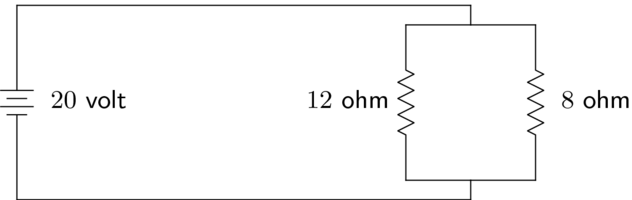
the electric current through the battery is $25/6$ amperes. Thus, the parallel portion is equivalent to a single resistor of $20/(25/6)=4.8$ ohms.

1. What is the equivalent resistance if we change the $12$ ohm resistor to $5$ ohms?
2. What is the equivalent resistance if the two are each $8$ ohms?
3. Find the formula for the equivalent resistance if the two resistors in parallel are $r_{1}$ ohms and $r_{2}$ ohms.

Answer

1. Using the variables from the earlier analysis,

   ${\begin{array}{*{3}{rc}r}i_{0}&-&i_{1}&-&i_{2}&=&0\\-i_{0}&+&i_{1}&+&i_{2}&=&0\\&&5i_{1}&&&=&20\\&&&&8i_{2}&=&20\\&&-5i_{1}&+&8i_{2}&=&0\end{array}}$

   The current flowing in each branch is then is $i_{2}=20/8=2.5$, $i_{1}=20/5=4$, and $i_{0}=13/2=6.5$, all in amperes. Thus the parallel portion is acting like a single resistor of size $20/(13/2)\approx 3.08$ ohms.
2. A similar analysis gives that is $i_{2}=i_{1}=20/8=4$ and $i_{0}=40/8=5$ amperes. The equivalent resistance is $20/5=4$ ohms.
3. Another analysis like the prior ones gives is $i_{2}=20/r_{2}$, $i_{1}=20/r_{1}$, and $i_{0}=20(r_{1}+r_{2})/(r_{1}r_{2})$, all in amperes. So the parallel portion is acting like a single resistor of size $20/i_{1}=r_{1}r_{2}/(r_{1}+r_{2})$ ohms. (This equation is often stated as: the equivalent resistance $r$ satisfies $1/r=(1/r_{1})+(1/r_{2})$.)

Problem 3

For the car dashboard example that opens this Topic, solve for these amperages (assume that all resistances are $2$ ohms).

1. If the driver is stepping on the brakes, so the brake lights are on, and no other circuit is closed.
2. If the hi-beam headlights and the brake lights are on.

Answer

1. The circuit looks like this.

   

2. The circuit looks like this.

   

Problem 4

Show that, in this Wheatstone Bridge,

$r_{2}/r_{1}$ equals $r_{4}/r_{3}$ if and only if the current flowing through $r_{g}$ is zero. (The way that this device is used in practice is that an unknown resistance at $r_{4}$ is compared to the other three $r_{1}$, $r_{2}$, and $r_{3}$. At $r_{g}$ is placed a meter that shows the current. The three resistances $r_{1}$, $r_{2}$, and $r_{3}$ are varied— typically they each have a calibrated knob— until the current in the middle reads $0$, and then the above equation gives the value of $r_{4}$.)

Answer

Kirchoff's Current Law, applied to the node where $r_{1}$, $r_{2}$, and $r_{g}$ come together, and also applied to the node where $r_{3}$, $r_{4}$, and $r_{g}$ come together gives these.

$i_{3}r_{3}-i_{g}r_{g}-i_{1}r_{1}=0$
$i_{4}r_{4}-i_{2}r_{2}+i_{g}r_{g}=0$

Assuming that $i_{g}$ is zero gives that $i_{1}=i_{2}$, $i_{3}=i_{4}$, that $i_{1}r_{1}=i_{3}r_{3}$, and that $i_{2}r_{2}=i_{4}r_{4}$. Then rearranging the last equality,

$r_{4}=(i_{2}r_{2})/i_{4}*(i_{3}r_{3})/(i_{1}r_{1})$

and cancelling the $i$'s gives the desired conclusion.

There are networks other than electrical ones, and we can ask how well Kirchoff's laws apply to them. The remaining questions consider an extension to networks of streets.

Problem 5

Consider this traffic circle.

This is the traffic volume, in units of cars per five minutes.

${\begin{array}{r|c|c|c}&{\textit {North}}&{\textit {Pier}}&{\textit {Main}}\\\hline {\textit {into}}&100&150&25\\{\textit {outof}}&75&150&50\end{array}}$

We can set up equations to model how the traffic flows.

1. Adapt Kirchoff's Current Law to this circumstance. Is it a reasonable modelling assumption?
2. Label the three between-road arcs in the circle with a variable. Using the (adapted) Current Law, for each of the three in-out intersections state an equation describing the traffic flow at that node.
3. Solve that system.
4. Interpret your solution.
5. Restate the Voltage Law for this circumstance. How reasonable is it?

Answer

1. An adaptation is: in any intersection the flow in equals the flow out. It does seem reasonable in this case, unless cars are stuck at an intersection for a long time.
2. We can label the flow in this way.

   

   Because $50$ cars leave via Main while $25$ cars enter, $i_{1}-25=i_{2}$. Similarly Pier's in/out balance means that $i_{2}=i_{3}$ and North gives $i_{3}+25=i_{1}$. We have this system.

   ${\begin{array}{*{3}{rc}r}i_{1}&-&i_{2}&&&=&25\\&i_{2}&-&i_{3}&=&0\\-i_{1}&&&+&i_{3}&=&-25\end{array}}$

3. The row operations $\rho _{1}+\rho _{2}$ and $rho_{2}+\rho _{3}$ lead to the conclusion that there are infinitely many solutions. With $i_{3}$ as the parameter,

   $\{{\begin{pmatrix}25+i_{3}\\i_{3}\\i_{3}\end{pmatrix}}\,{\big |}\,i_{3}\in \mathbb {R} \}$

   of course, since the problem is stated in number of cars, we might restrict $i_{3}$ to be a natural number.
4. If we picture an initially-empty circle with the given input/output behavior, we can superimpose a $z_{3}$-many cars circling endlessly to get a new solution.
5. A suitable restatement might be: the number of cars entering the circle must equal the number of cars leaving. The reasonableness of this one is not as clear. Over the five minute time period it could easily work out that a half dozen more cars entered than left, although the into/out of table in the problem statement does have that this property is satisfied. In any event it is of no help in getting a unique solution since for that we need to know the number of cars circling endlessly.

Problem 6

This is a network of streets.

The hourly flow of cars into this network's entrances, and out of its exits can be observed.

${\begin{array}{r|c|c|c|c|c}&{\textit {east\ Winooski}}&{\textit {west\ Winooski}}&{\textit {Willow}}&{\textit {Jay}}&{\textit {Shelburne}}\\\hline {\text{into}}&80&50&65&--&40\\{\text{out of}}&30&5&70&55&75\end{array}}$

(Note that to reach Jay a car must enter the network via some other road first, which is why there is no "into Jay" entry in the table. Note also that over a long period of time, the total in must approximately equal the total out, which is why both rows add to $235$ cars.) Once inside the network, the traffic may flow in different ways, perhaps filling Willow and leaving Jay mostly empty, or perhaps flowing in some other way. Kirchhoff's Laws give the limits on that freedom.

1. Determine the restrictions on the flow inside this network of streets by setting up a variable for each block, establishing the equations, and solving them. Notice that some streets are one-way only. (Hint: this will not yield a unique solution, since traffic can flow through this network in various ways; you should get at least one free variable.)
2. Suppose that some construction is proposed for Winooski Avenue East between Willow and Jay, so traffic on that block will be reduced. What is the least amount of traffic flow that can be allowed on that block without disrupting the hourly flow into and out of the network?

Answer

1. Here is a variable for each unknown block; each known block has the flow shown.

   

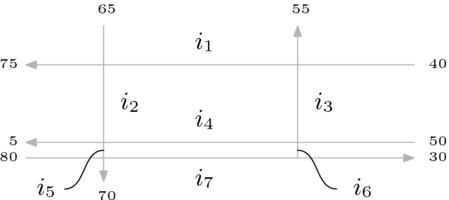
   We apply Kirchoff's principle that the flow into the intersection of Willow and Shelburne must equal the flow out to get $i_{1}+25=i_{2}+125$. Doing the intersections from right to left and top to bottom gives these equations.

   ${\begin{array}{*{7}{rc}r}i_{1}&-&i_{2}&&&&&&&&&&&=&10\\-i_{1}&&&+&i_{3}&&&&&&&&&=&15\\&&i_{2}&&&+&i_{4}&&&&&&&=&5\\&&&&-i_{3}&-&i_{4}&&&+&i_{6}&&&=&-50\\&&&&&&&&i_{5}&&&-&i_{7}&=&-10\\&&&&&&&&&&-i_{6}&+&i_{7}&=&30\end{array}}$

   The row operation $\rho _{1}+\rho _{2}$ followed by $\rho _{2}+\rho _{3}$ then $\rho _{3}+\rho _{4}$ and $\rho _{4}+\rho _{5}$ and finally $\rho _{5}+\rho _{6}$ result in this system.

   ${\begin{array}{*{7}{rc}r}i_{1}&-&i_{2}&&&&&&&&&&&=&10\\&&-i_{2}&+&i_{3}&&&&&&&&&=&25\\&&&&i_{3}&+&i_{4}&-&i_{5}&&&&&=&30\\&&&&&&&&-i_{5}&+&i_{6}&&&=&-20\\&&&&&&&&&&-i_{6}&+&i_{7}&=&-30\\&&&&&&&&&&&&0&=&0\end{array}}$

   Since the free variables are $i_{4}$ and $i_{7}$ we take them as parameters.

   ${\begin{array}{rl}i_{6}&=i_{7}-30\\i_{5}&=i_{6}+20=(i_{7}-30)+20=i_{7}-10\\i_{3}&=-i_{4}+i_{5}+30=-i_{4}+(i_{7}-10)+30=-i_{4}+i_{7}+20\\i_{2}&=i_{3}-25=(-i_{4}+i_{7}+20)-25=-i_{4}+i_{7}-5\\i_{1}&=i_{2}+10=(-i_{4}+i_{7}-5)+10=-i_{4}+i_{7}+5\end{array}}$

   Obviously $i_{4}$ and $i_{7}$ have to be positive, and in fact the first equation shows that $i_{7}$ must be at least $30$. If we start with $i_{7}$, then the $i_{2}$ equation shows that $0\leq i_{4}\leq i_{7}-5$.

2. We cannot take $i_{7}$ to be zero or else $i_{6}$ will be negative (this would mean cars going the wrong way on the one-way street Jay). We can, however, take $i_{7}$ to be as small as $30$, and then there are many suitable $i_{4}$'s. For instance, the solution

   $(i_{1},i_{2},i_{3},i_{4},i_{5},i_{6},i_{7})=(35,25,50,0,20,0,30)$

   results from choosing $i_{4}=0$.