Linear Algebra/Definition and Examples of Isomorphisms/Solutions

Solutions

This exercise is recommended for all readers.

Problem 1

Verify, using Example 1.4 as a model, that the two correspondences given before the definition are isomorphisms.

Answer

Call the map $f$ .
$(\begin{matrix} a & b \end{matrix}) \overset{f}{⟼} (\begin{matrix} a \\ b \end{matrix})$
It is one-to-one because if $f$ sends two members of the domain to the same image, that is, if $f ((\begin{matrix} a & b \end{matrix})) = f ((\begin{matrix} c & d \end{matrix}))$ , then the definition of $f$ gives that
$(\begin{matrix} a \\ b \end{matrix}) = (\begin{matrix} c \\ d \end{matrix})$
and since column vectors are equal only if they have equal components, we have that $a = c$ and that $b = d$ . Thus, if $f$ maps two row vectors from the domain to the same column vector then the two row vectors are equal: $(\begin{matrix} a & b \end{matrix}) = (\begin{matrix} c & d \end{matrix})$ . To show that $f$ is onto we must show that any member of the codomain $ℝ^{2}$ is the image under $f$ of some row vector. That's easy;
$(\begin{matrix} x \\ y \end{matrix})$
is $f ((\begin{matrix} x & y \end{matrix}))$ . The computation for preservation of addition is this.
$f ((\begin{matrix} a & b \end{matrix}) + (\begin{matrix} c & d \end{matrix})) = f ((\begin{matrix} a + c & b + d \end{matrix})) = (\begin{matrix} a + c \\ b + d \end{matrix}) = (\begin{matrix} a \\ b \end{matrix}) + (\begin{matrix} c \\ d \end{matrix}) = f ((\begin{matrix} a & b \end{matrix})) + f ((\begin{matrix} c & d \end{matrix}))$
The computation for preservation of scalar multiplication is similar.
$f (r \cdot (\begin{matrix} a & b \end{matrix})) = f ((\begin{matrix} r a & r b \end{matrix})) = (\begin{matrix} r a \\ r b \end{matrix}) = r \cdot (\begin{matrix} a \\ b \end{matrix}) = r \cdot f ((\begin{matrix} a & b \end{matrix}))$
Denote the map from Example 1.2 by $f$ . To show that it is one-to-one, assume that $f (a_{0} + a_{1} x + a_{2} x^{2}) = f (b_{0} + b_{1} x + b_{2} x^{2})$ . Then by the definition of the function,
$(\begin{matrix} a_{0} \\ a_{1} \\ a_{2} \end{matrix}) = (\begin{matrix} b_{0} \\ b_{1} \\ b_{2} \end{matrix})$
and so $a_{0} = b_{0}$ and $a_{1} = b_{1}$ and $a_{2} = b_{2}$ . Thus $a_{0} + a_{1} x + a_{2} x^{2} = b_{0} + b_{1} x + b_{2} x^{2}$ , and consequently $f$ is one-to-one. The function $f$ is onto because there is a polynomial sent to
$(\begin{matrix} a \\ b \\ c \end{matrix})$
by $f$ , namely, $a + b x + c x^{2}$ . As for structure, this shows that $f$ preserves addition
$\begin{matrix} f ((a_{0} + a_{1} x + a_{2} x^{2}) + (b_{0} + b_{1} x + b_{2} x^{2})) & = f ((a_{0} + b_{0}) + (a_{1} + b_{1}) x + (a_{2} + b_{2}) x^{2}) \\ = (\begin{matrix} a_{0} + b_{0} \\ a_{1} + b_{1} \\ a_{2} + b_{2} \end{matrix}) \\ = (\begin{matrix} a_{0} \\ a_{1} \\ a_{2} \end{matrix}) + (\begin{matrix} b_{0} \\ b_{1} \\ b_{2} \end{matrix}) \\ = f (a_{0} + a_{1} x + a_{2} x^{2}) + f (b_{0} + b_{1} x + b_{2} x^{2}) \end{matrix}$
and this shows
$\begin{matrix} f (r (a_{0} + a_{1} x + a_{2} x^{2})) & = f ((r a_{0}) + (r a_{1}) x + (r a_{2}) x^{2}) \\ = (\begin{matrix} r a_{0} \\ r a_{1} \\ r a_{2} \end{matrix}) \\ = r \cdot (\begin{matrix} a_{0} \\ a_{1} \\ a_{2} \end{matrix}) \\ = r f (a_{0} + a_{1} x + a_{2} x^{2}) \end{matrix}$
that it preserves scalar multiplication.

This exercise is recommended for all readers.

Problem 2

For the map $f : 𝒫_{1} \to ℝ^{2}$ given by

a + b x \overset{f}{⟼} (\begin{matrix} a - b \\ b \end{matrix})

Find the image of each of these elements of the domain.

$3 - 2 x$
$2 + 2 x$
$x$

Show that this map is an isomorphism.

Answer

These are the images.

$(\begin{matrix} 5 \\ - 2 \end{matrix})$
$(\begin{matrix} 0 \\ 2 \end{matrix})$
$(\begin{matrix} - 1 \\ 1 \end{matrix})$

To prove that $f$ is one-to-one, assume that it maps two linear polynomials to the same image $f (a_{1} + b_{1} x) = f (a_{2} + b_{2} x)$ . Then

(\begin{matrix} a_{1} - b_{1} \\ b_{1} \end{matrix}) = (\begin{matrix} a_{2} - b_{2} \\ b_{2} \end{matrix})

and so, since column vectors are equal only when their components are equal, $b_{1} = b_{2}$ and $a_{1} = a_{2}$ . That shows that the two linear polynomials are equal, and so $f$ is one-to-one.

To show that $f$ is onto, note that this member of the codomain

(\begin{matrix} s \\ t \end{matrix})

is the image of this member of the domain $(s + t) + t x$ .

To check that $f$ preserves structure, we can use item 2 of Lemma 1.9.

\begin{matrix} f (c_{1} \cdot (a_{1} + b_{1} x) + c_{2} \cdot (a_{2} + b_{2} x)) & = f ((c_{1} a_{1} + c_{2} a_{2}) + (c_{1} b_{1} + c_{2} b_{2}) x) \\ = (\begin{matrix} (c_{1} a_{1} + c_{2} a_{2}) - (c_{1} b_{1} + c_{2} b_{2}) \\ c_{1} b_{1} + c_{2} b_{2} \end{matrix}) \\ = c_{1} \cdot (\begin{matrix} a_{1} - b_{1} \\ b_{1} \end{matrix}) + c_{2} \cdot (\begin{matrix} a_{2} - b_{2} \\ b_{2} \end{matrix}) \\ = c_{1} \cdot f (a_{1} + b_{1} x) + c_{2} \cdot f (a_{2} + b_{2} x) \end{matrix}

Problem 3

Show that the natural map $f_{1}$ from Example 1.5 is an isomorphism.

Answer

To verify it is one-to-one, assume that $f_{1} (c_{1} x + c_{2} y + c_{3} z) = f_{1} (d_{1} x + d_{2} y + d_{3} z)$ . Then $c_{1} + c_{2} x + c_{3} x^{2} = d_{1} + d_{2} x + d_{3} x^{2}$ by the definition of $f_{1}$ . Members of $𝒫_{2}$ are equal only when they have the same coefficients, so this implies that $c_{1} = d_{1}$ and $c_{2} = d_{2}$ and $c_{3} = d_{3}$ . Therefore $f_{1} (c_{1} x + c_{2} y + c_{3} z) = f_{1} (d_{1} x + d_{2} y + d_{3} z)$ implies that $c_{1} x + c_{2} y + c_{3} z = d_{1} x + d_{2} y + d_{3} z$ , and so $f_{1}$ is one-to-one.

To verify that it is onto, consider an arbitrary member of the codomain $a_{1} + a_{2} x + a_{3} x^{2}$ and observe that it is indeed the image of a member of the domain, namely, it is $f_{1} (a_{1} x + a_{2} y + a_{3} z)$ . (For instance, $0 + 3 x + 6 x^{2} = f_{1} (0 x + 3 y + 6 z)$ .)

The computation checking that $f_{1}$ preserves addition is this.

\begin{matrix} f_{1} ((c_{1} x + c_{2} y + c_{3} z) + (d_{1} x + d_{2} y + d_{3} z)) & = f_{1} ((c_{1} + d_{1}) x + (c_{2} + d_{2}) y + (c_{3} + d_{3}) z) \\ = (c_{1} + d_{1}) + (c_{2} + d_{2}) x + (c_{3} + d_{3}) x^{2} \\ = (c_{1} + c_{2} x + c_{3} x^{2}) + (d_{1} + d_{2} x + d_{3} x^{2}) \\ = f_{1} (c_{1} x + c_{2} y + c_{3} z) + f_{1} (d_{1} x + d_{2} y + d_{3} z) \end{matrix}

The check that $f_{1}$ preserves scalar multiplication is this.

\begin{matrix} f_{1} (r \cdot (c_{1} x + c_{2} y + c_{3} z)) & = f_{1} ((r c_{1}) x + (r c_{2}) y + (r c_{3}) z) \\ = (r c_{1}) + (r c_{2}) x + (r c_{3}) x^{2} \\ = r \cdot (c_{1} + c_{2} x + c_{3} x^{2}) \\ = r \cdot f_{1} (c_{1} x + c_{2} y + c_{3} z) \end{matrix}

This exercise is recommended for all readers.

Problem 4

Decide whether each map is an isomorphism (if it is an isomorphism then prove it and if it isn't then state a condition that it fails to satisfy).

$f : ℳ_{2 \times 2} \to ℝ$ given by
$(\begin{matrix} a & b \\ c & d \end{matrix}) \mapsto a d - b c$
$f : ℳ_{2 \times 2} \to ℝ^{4}$ given by
$(\begin{matrix} a & b \\ c & d \end{matrix}) \mapsto (\begin{matrix} a + b + c + d \\ a + b + c \\ a + b \\ a \end{matrix})$
$f : ℳ_{2 \times 2} \to 𝒫_{3}$ given by
$(\begin{matrix} a & b \\ c & d \end{matrix}) \mapsto c + (d + c) x + (b + a) x^{2} + a x^{3}$
$f : ℳ_{2 \times 2} \to 𝒫_{3}$ given by
$(\begin{matrix} a & b \\ c & d \end{matrix}) \mapsto c + (d + c) x + (b + a + 1) x^{2} + a x^{3}$

Answer

No; this map is not one-to-one. In particular, the matrix of all zeroes is mapped to the same image as the matrix of all ones.
Yes, this is an isomorphism. It is one-to-one:
$if f ((\begin{matrix} a_{1} & b_{1} \\ c_{1} & d_{1} \end{matrix})) = f ((\begin{matrix} a_{2} & b_{2} \\ c_{2} & d_{2} \end{matrix})) then (\begin{matrix} a_{1} + b_{1} + c_{1} + d_{1} \\ a_{1} + b_{1} + c_{1} \\ a_{1} + b_{1} \\ a_{1} \end{matrix}) = (\begin{matrix} a_{2} + b_{2} + c_{2} + d_{2} \\ a_{2} + b_{2} + c_{2} \\ a_{2} + b_{2} \\ a_{2} \end{matrix})$
gives that $a_{1} = a_{2}$ , and that $b_{1} = b_{2}$ , and that $c_{1} = c_{2}$ , and that $d_{1} = d_{2}$ . It is onto, since this shows
$(\begin{matrix} x \\ y \\ z \\ w \end{matrix}) = f ((\begin{matrix} w & z - w \\ y - z & x - y \end{matrix}))$
that any four-tall vector is the image of a $2 \times 2$ matrix. Finally, it preserves combinations
$\begin{matrix} f (r_{1} \cdot (\begin{matrix} a_{1} & b_{1} \\ c_{1} & d_{1} \end{matrix}) + r_{2} \cdot (\begin{matrix} a_{2} & b_{2} \\ c_{2} & d_{2} \end{matrix})) & = f ((\begin{matrix} r_{1} a_{1} + r_{2} a_{2} & r_{1} b_{1} + r_{2} b_{2} \\ r_{1} c_{1} + r_{2} c_{2} & r_{1} d_{1} + r_{2} d_{2} \end{matrix})) \\ = (\begin{matrix} r_{1} a_{1} + \dots + r_{2} d_{2} \\ r_{1} a_{1} + \dots + r_{2} c_{2} \\ r_{1} a_{1} + \dots + r_{2} b_{2} \\ r_{1} a_{1} + r_{2} a_{2} \end{matrix}) \\ = r_{1} \cdot (\begin{matrix} a_{1} + \dots + d_{1} \\ a_{1} + \dots + c_{1} \\ a_{1} + b_{1} \\ a_{1} \end{matrix}) + r_{2} \cdot (\begin{matrix} a_{2} + \dots + d_{2} \\ a_{2} + \dots + c_{2} \\ a_{2} + b_{2} \\ a_{2} \end{matrix}) \\ = r_{1} \cdot f ((\begin{matrix} a_{1} & b_{1} \\ c_{1} & d_{1} \end{matrix})) + r_{2} \cdot f ((\begin{matrix} a_{2} & b_{2} \\ c_{2} & d_{2} \end{matrix})) \end{matrix}$
and so item 2 of Lemma 1.9 shows that it preserves structure.
Yes, it is an isomorphism. To show that it is one-to-one, we suppose that two members of the domain have the same image under $f$ .
$f ((\begin{matrix} a_{1} & b_{1} \\ c_{1} & d_{1} \end{matrix})) = f ((\begin{matrix} a_{2} & b_{2} \\ c_{2} & d_{2} \end{matrix}))$
This gives, by the definition of $f$ , that $c_{1} + (d_{1} + c_{1}) x + (b_{1} + a_{1}) x^{2} + a_{1} x^{3} = c_{2} + (d_{2} + c_{2}) x + (b_{2} + a_{2}) x^{2} + a_{2} x^{3}$ and then the fact that polynomials are equal only when their coefficients are equal gives a set of linear equations
$\begin{matrix} c_{1} & = c_{2} \\ d_{1} + c_{1} & = d_{2} + c_{2} \\ b_{1} + a_{1} & = b_{2} + a_{2} \\ a_{1} & = a_{2} \end{matrix}$
that has only the solution $a_{1} = a_{2}$ , $b_{1} = b_{2}$ , $c_{1} = c_{2}$ , and $d_{1} = d_{2}$ . To show that $f$ is onto, we note that $p + q x + r x^{2} + s x^{3}$ is the image under $f$ of this matrix.
$(\begin{matrix} s & r - s \\ p & q - p \end{matrix})$
We can check that $f$ preserves structure by using item 2 of Lemma 1.9.
$\begin{matrix} f (r_{1} \cdot (\begin{matrix} a_{1} & b_{1} \\ c_{1} & d_{1} \end{matrix}) + r_{2} \cdot (\begin{matrix} a_{2} & b_{2} \\ c_{2} & d_{2} \end{matrix})) & = f ((\begin{matrix} r_{1} a_{1} + r_{2} a_{2} & r_{1} b_{1} + r_{2} b_{2} \\ r_{1} c_{1} + r_{2} c_{2} & r_{1} d_{1} + r_{2} d_{2} \end{matrix})) \\ = \begin{matrix} (r_{1} c_{1} + r_{2} c_{2}) + (r_{1} d_{1} + r_{2} d_{2} + r_{1} c_{1} + r_{2} c_{2}) x \\ + (r_{1} b_{1} + r_{2} b_{2} + r_{1} a_{1} + r_{2} a_{2}) x^{2} + (r_{1} a_{1} + r_{2} a_{2}) x^{3} \end{matrix} \\ = \begin{matrix} r_{1} \cdot (c_{1} + (d_{1} + c_{1}) x + (b_{1} + a_{1}) x^{2} + a_{1} x^{3}) \\ + r_{2} \cdot (c_{2} + (d_{2} + c_{2}) x + (b_{2} + a_{2}) x^{2} + a_{2} x^{3}) \end{matrix} \\ = r_{1} \cdot f ((\begin{matrix} a_{1} & b_{1} \\ c_{1} & d_{1} \end{matrix})) + r_{2} \cdot f ((\begin{matrix} a_{2} & b_{2} \\ c_{2} & d_{2} \end{matrix})) \end{matrix}$
No, this map does not preserve structure. For instance, it does not send the zero matrix to the zero polynomial.

Problem 5

Show that the map $f : ℝ^{1} \to ℝ^{1}$ given by $f (x) = x^{3}$ is one-to-one and onto.Is it an isomorphism?

Answer

It is one-to-one and onto, a correspondence, because it has an inverse (namely, $f^{- 1} (x) = \sqrt[3]{x}$ ). However, it is not an isomorphism. For instance, $f (1) + f (1) \neq f (1 + 1)$ .

This exercise is recommended for all readers.

Problem 6

Refer to Example 1.1. Produce two more isomorphisms (of course, that they satisfy the conditions in the definition of isomorphism must be verified).

Answer

Many maps are possible. Here are two.

(\begin{matrix} a & b \end{matrix}) \mapsto (\begin{matrix} b \\ a \end{matrix}) and (\begin{matrix} a & b \end{matrix}) \mapsto (\begin{matrix} 2 a \\ b \end{matrix})

The verifications are straightforward adaptations of the others above.

Problem 7

Refer to Example 1.2. Produce two more isomorphisms (and verify that they satisfy the conditions).

Answer

Here are two.

a_{0} + a_{1} x + a_{2} x^{2} \mapsto (\begin{matrix} a_{1} \\ a_{0} \\ a_{2} \end{matrix}) and a_{0} + a_{1} x + a_{2} x^{2} \mapsto (\begin{matrix} a_{0} + a_{1} \\ a_{1} \\ a_{2} \end{matrix})

Verification is straightforward (for the second, to show that it is onto, note that

(\begin{matrix} s \\ t \\ u \end{matrix})

is the image of $(s - t) + t x + u x^{2}$ ).

This exercise is recommended for all readers.

Problem 8

Show that, although $ℝ^{2}$ is not itself a subspace of $ℝ^{3}$ , it is isomorphic to the $x y$ -plane subspace of $ℝ^{3}$ .

Answer

The space $ℝ^{2}$ is not a subspace of $ℝ^{3}$ because it is not a subset of $ℝ^{3}$ . The two-tall vectors in $ℝ^{2}$ are not members of $ℝ^{3}$ .

The natural isomorphism $ι : ℝ^{2} \to ℝ^{3}$ (called the injection map) is this.

(\begin{matrix} x \\ y \end{matrix}) \overset{ι}{⟼} (\begin{matrix} x \\ y \\ 0 \end{matrix})

This map is one-to-one because

f ((\begin{matrix} x_{1} \\ y_{1} \end{matrix})) = f ((\begin{matrix} x_{2} \\ y_{2} \end{matrix})) implies (\begin{matrix} x_{1} \\ y_{1} \\ 0 \end{matrix}) = (\begin{matrix} x_{2} \\ y_{2} \\ 0 \end{matrix})

which in turn implies that $x_{1} = x_{2}$ and $y_{1} = y_{2}$ , and therefore the initial two two-tall vectors are equal.

Because

(\begin{matrix} x \\ y \\ 0 \end{matrix}) = f ((\begin{matrix} x \\ y \end{matrix}))

this map is onto the $x y$ -plane.

To show that this map preserves structure, we will use item 2 of Lemma 1.9 and show

f (c_{1} \cdot (\begin{matrix} x_{1} \\ y_{1} \end{matrix}) + c_{2} \cdot (\begin{matrix} x_{2} \\ y_{2} \end{matrix})) = f ((\begin{matrix} c_{1} x_{1} + c_{2} x_{2} \\ c_{1} y_{1} + c_{2} y_{2} \end{matrix})) = (\begin{matrix} c_{1} x_{1} + c_{2} x_{2} \\ c_{1} y_{1} + c_{2} y_{2} \\ 0 \end{matrix})

= c_{1} \cdot (\begin{matrix} x_{1} \\ y_{1} \\ 0 \end{matrix}) + c_{2} \cdot (\begin{matrix} x_{2} \\ y_{2} \\ 0 \end{matrix}) = c_{1} \cdot f ((\begin{matrix} x_{1} \\ y_{1} \end{matrix})) + c_{2} \cdot f ((\begin{matrix} x_{2} \\ y_{2} \end{matrix}))

that it preserves combinations of two vectors.

Problem 9

Find two isomorphisms between $ℝ^{16}$ and $ℳ_{4 \times 4}$ .

Answer

Here are two:

(\begin{matrix} r_{1} \\ r_{2} \\ ⋮ \\ r_{16} \end{matrix}) \mapsto (\begin{matrix} r_{1} & r_{2} & \dots \\ \dots & r_{16} \end{matrix}) and (\begin{matrix} r_{1} \\ r_{2} \\ ⋮ \\ r_{16} \end{matrix}) \mapsto (\begin{matrix} r_{1} \\ r_{2} \\ ⋮ & ⋮ \\ r_{16} \end{matrix})

Verification that each is an isomorphism is easy.

This exercise is recommended for all readers.

Problem 10

For what $k$ is $ℳ_{m \times n}$ isomorphic to $ℝ^{k}$ ?

Answer

When $k$ is the product $k = m n$ , here is an isomorphism.

(\begin{matrix} r_{1} & r_{2} & \dots \\ ⋮ \\ \dots & r_{m \cdot n} \end{matrix}) \mapsto (\begin{matrix} r_{1} \\ r_{2} \\ ⋮ \\ r_{m \cdot n} \end{matrix})

Checking that this is an isomorphism is easy.

Problem 11

For what $k$ is $𝒫_{k}$ isomorphic to $ℝ^{n}$ ?

Answer

If $n \geq 1$ then $𝒫_{n - 1} ≅ ℝ^{n}$ . (If we take $𝒫_{- 1}$ and $ℝ^{0}$ to be trivial vector spaces, then the relationship extends one dimension lower.) The natural isomorphism between them is this.

a_{0} + a_{1} x + \dots + a_{n - 1} x^{n - 1} \mapsto (\begin{matrix} a_{0} \\ a_{1} \\ ⋮ \\ a_{n - 1} \end{matrix})

Checking that it is an isomorphism is straightforward.

Problem 12

Prove that the map in Example 1.7, from $𝒫_{5}$ to $𝒫_{5}$ given by $p (x) \mapsto p (x - 1)$ , is a vector space isomorphism.

Answer

This is the map, expanded.

\begin{matrix} f (a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} + a_{4} x^{4} + a_{5} x^{5}) & = \begin{matrix} a_{0} + a_{1} (x - 1) + a_{2} (x - 1)^{2} + a_{3} (x - 1)^{3} \\ + a_{4} (x - 1)^{4} + a_{5} (x - 1)^{5} \end{matrix} \\ = \begin{matrix} a_{0} + a_{1} (x - 1) + a_{2} (x^{2} - 2 x + 1) \\ + a_{3} (x^{3} - 3 x^{2} + 3 x - 1) \\ + a_{4} (x^{4} - 4 x^{3} + 6 x^{2} - 4 x + 1) \\ + a_{5} (x^{5} - 5 x^{4} + 10 x^{3} - 10 x^{2} + 5 x - 1) \end{matrix} \\ = \begin{matrix} (a_{0} - a_{1} + a_{2} - a_{3} + a_{4} - a_{5}) \\ + (a_{1} - 2 a_{2} + 3 a_{3} - 4 a_{4} + 5 a_{5}) x \\ + (a_{2} - 3 a_{3} + 6 a_{4} - 10 a_{5}) x^{2} + (a_{3} - 4 a_{4} + 10 a_{5}) x^{3} \\ + (a_{4} - 5 a_{5}) x^{4} + a_{5} x^{5} \end{matrix} \end{matrix}

To finish checking that it is an isomorphism, we apply item 2 of Lemma 1.9 and show that it preserves linear combinations of two polynomials. Briefly, the check goes like this.

f (c \cdot (a_{0} + a_{1} x + \dots + a_{5} x^{5}) + d \cdot (b_{0} + b_{1} x + \dots + b_{5} x^{5}))

= \dots = (c a_{0} - c a_{1} + c a_{2} - c a_{3} + c a_{4} - c a_{5} + d b_{0} - d b_{1} + d b_{2} - d b_{3} + d b_{4} - d b_{5}) + \dots + (c a_{5} + d b_{5}) x^{5}

= \dots = c \cdot f (a_{0} + a_{1} x + \dots + a_{5} x^{5}) + d \cdot f (b_{0} + b_{1} x + \dots + b_{5} x^{5})

Problem 13

Why, in Lemma 1.8, must there be a $\vec{v} \in V$ ? That is, why must $V$ be nonempty?

Answer

No vector space has the empty set underlying it. We can take $\vec{v}$ to be the zero vector.

Problem 14

Are any two trivial spaces isomorphic?

Answer

Yes; where the two spaces are ${\vec{a}}$ and ${\vec{b}}$ , the map sending $\vec{a}$ to $\vec{b}$ is clearly one-to-one and onto, and also preserves what little structure there is.

Problem 15

In the proof of Lemma 1.9, what about the zero-summands case (that is, if $n$ is zero)?

Answer

A linear combination of $n = 0$ vectors adds to the zero vector and so Lemma 1.8 shows that the three statements are equivalent in this case.

Problem 16

Show that any isomorphism $f : 𝒫_{0} \to ℝ^{1}$ has the form $a \mapsto k a$ for some nonzero real number $k$ .

Answer

Consider the basis $⟨ 1 ⟩$ for $𝒫_{0}$ and let $f (1) \in ℝ$ be $k$ . For any $a \in 𝒫_{0}$ we have that $f (a) = f (a \cdot 1) = a f (1) = a k$ and so $f$ 's action is multiplication by $k$ . Note that $k \neq 0$ or else the map is not one-to-one. (Incidentally, any such map $a \mapsto k a$ is an isomorphism, as is easy to check.)

This exercise is recommended for all readers.

Problem 17

These prove that isomorphism is an equivalence relation.

Show that the identity map $id : V \to V$ is an isomorphism. Thus, any vector space is isomorphic to itself.
Show that if $f : V \to W$ is an isomorphism then so is its inverse $f^{- 1} : W \to V$ . Thus, if $V$ is isomorphic to $W$ then also $W$ is isomorphic to $V$ .
Show that a composition of isomorphisms is an isomorphism: if $f : V \to W$ is an isomorphism and $g : W \to U$ is an isomorphism then so also is $g \circ f : V \to U$ . Thus, if $V$ is isomorphic to $W$ and $W$ is isomorphic to $U$ , then also $V$ is isomorphic to $U$ .

Answer

In each item, following item 2 of Lemma 1.9, we show that the map preserves structure by showing that the it preserves linear combinations of two members of the domain.

The identity map is clearly one-to-one and onto. For linear combinations the check is easy.
$id (c_{1} \cdot {\vec{v}}_{1} + c_{2} \cdot {\vec{v}}_{2}) = c_{1} {\vec{v}}_{1} + c_{2} {\vec{v}}_{2} = c_{1} \cdot id ({\vec{v}}_{1}) + c_{2} \cdot id ({\vec{v}}_{2})$
The inverse of a correspondence is also a correspondence (as stated in the appendix), so we need only check that the inverse preserves linear combinations. Assume that ${\vec{w}}_{1} = f ({\vec{v}}_{1})$ (so $f^{- 1} ({\vec{w}}_{1}) = {\vec{v}}_{1}$ ) and assume that ${\vec{w}}_{2} = f ({\vec{v}}_{2})$ .
$\begin{matrix} f^{- 1} (c_{1} \cdot {\vec{w}}_{1} + c_{2} \cdot {\vec{w}}_{2}) & = f^{- 1} (c_{1} \cdot f ({\vec{v}}_{1}) + c_{2} \cdot f ({\vec{v}}_{2})) \\ = f^{- 1} (f (c_{1} {\vec{v}}_{1} + c_{2} {\vec{v}}_{2})) \\ = c_{1} {\vec{v}}_{1} + c_{2} {\vec{v}}_{2} \\ = c_{1} \cdot f^{- 1} ({\vec{w}}_{1}) + c_{2} \cdot f^{- 1} ({\vec{w}}_{2}) \end{matrix}$
The composition of two correspondences is a correspondence (as stated in the appendix), so we need only check that the composition map preserves linear combinations.
$\begin{matrix} g \circ f (c_{1} \cdot {\vec{v}}_{1} + c_{2} \cdot {\vec{v}}_{2}) & = g (f (c_{1} {\vec{v}}_{1} + c_{2} {\vec{v}}_{2})) \\ = g (c_{1} \cdot f ({\vec{v}}_{1}) + c_{2} \cdot f ({\vec{v}}_{2})) \\ = c_{1} \cdot g (f ({\vec{v}}_{1})) + c_{2} \cdot g (f ({\vec{v}}_{2})) \\ = c_{1} \cdot g \circ f ({\vec{v}}_{1}) + c_{2} \cdot g \circ f ({\vec{v}}_{2}) \end{matrix}$

Problem 18

Suppose that $f : V \to W$ preserves structure. Show that $f$ is one-to-one if and only if the unique member of $V$ mapped by $f$ to ${\vec{0}}_{W}$ is ${\vec{0}}_{V}$ .

Answer

One direction is easy: by definition, if $f$ is one-to-one then for any $\vec{w} \in W$ at most one $\vec{v} \in V$ has $f (\vec{v}) = \vec{w}$ , and so in particular, at most one member of $V$ is mapped to ${\vec{0}}_{W}$ . The proof of Lemma 1.8 does not use the fact that the map is a correspondence and therefore shows that any structure-preserving map $f$ sends ${\vec{0}}_{V}$ to ${\vec{0}}_{W}$ .

For the other direction, assume that the only member of $V$ that is mapped to ${\vec{0}}_{W}$ is ${\vec{0}}_{V}$ . To show that $f$ is one-to-one assume that $f ({\vec{v}}_{1}) = f ({\vec{v}}_{2})$ . Then $f ({\vec{v}}_{1}) - f ({\vec{v}}_{2}) = {\vec{0}}_{W}$ and so $f ({\vec{v}}_{1} - {\vec{v}}_{2}) = {\vec{0}}_{W}$ . Consequently ${\vec{v}}_{1} - {\vec{v}}_{2} = {\vec{0}}_{V}$ , so ${\vec{v}}_{1} = {\vec{v}}_{2}$ , and so $f$ is one-to-one.

Problem 19

Suppose that $f : V \to W$ is an isomorphism. Prove that the set ${{\vec{v}}_{1}, \dots, {\vec{v}}_{k}} \subseteq V$ is linearly dependent if and only if the set of images ${f ({\vec{v}}_{1}), \dots, f ({\vec{v}}_{k})} \subseteq W$ is linearly dependent.

Answer

We will prove something stronger— not only is the existence of a dependence preserved by isomorphism, but each instance of a dependence is preserved, that is,

{\vec{v}}_{i} = c_{1} {\vec{v}}_{1} + \dots + c_{i - 1} {\vec{v}}_{i - 1} + c_{i + 1} {\vec{v}}_{i + 1} + \dots + c_{k} {\vec{v}}_{k}

⟺ f ({\vec{v}}_{i}) = c_{1} f ({\vec{v}}_{1}) + \dots + c_{i - 1} f ({\vec{v}}_{i - 1}) + c_{i + 1} f ({\vec{v}}_{i + 1}) + \dots + c_{k} f ({\vec{v}}_{k}) .

The $⟹$ direction of this statement holds by item 3 of Lemma 1.9. The $⟸$ direction holds by regrouping

\begin{matrix} f ({\vec{v}}_{i}) & = c_{1} f ({\vec{v}}_{1}) + \dots + c_{i - 1} f ({\vec{v}}_{i - 1}) + c_{i + 1} f ({\vec{v}}_{i + 1}) + \dots + c_{k} f ({\vec{v}}_{k}) \\ = f (c_{1} {\vec{v}}_{1} + \dots + c_{i - 1} {\vec{v}}_{i - 1} + c_{i + 1} {\vec{v}}_{i + 1} + \dots + c_{k} {\vec{v}}_{k}) \end{matrix}

and applying the fact that $f$ is one-to-one, and so for the two vectors ${\vec{v}}_{i}$ and $c_{1} {\vec{v}}_{1} + \dots + c_{i - 1} {\vec{v}}_{i - 1} + c_{i + 1} {\vec{v}}_{i + 1} + \dots + c_{k} {\vec{v}}_{k}$ to be mapped to the same image by $f$ , they must be equal.

This exercise is recommended for all readers.

Problem 20

Show that each type of map from Example 1.6 is an automorphism.

Dilation $d_{s}$ by a nonzero scalar $s$ .
Rotation $t_{θ}$ through an angle $θ$ .
Reflection $f_{ℓ}$ over a line through the origin.

Hint. For the second and third items, polar coordinates are useful.

Answer

This map is one-to-one because if $d_{s} ({\vec{v}}_{1}) = d_{s} ({\vec{v}}_{2})$ then by definition of the map, $s \cdot {\vec{v}}_{1} = s \cdot {\vec{v}}_{2}$ and so ${\vec{v}}_{1} = {\vec{v}}_{2}$ , as $s$ is nonzero. This map is onto as any $\vec{w} \in ℝ^{2}$ is the image of $\vec{v} = (1 / s) \cdot \vec{w}$ (again, note that $s$ is nonzero). (Another way to see that this map is a correspondence is to observe that it has an inverse: the inverse of $d_{s}$ is $d_{1 / s}$ .) To finish, note that this map preserves linear combinations
$d_{s} (c_{1} \cdot {\vec{v}}_{1} + c_{2} \cdot {\vec{v}}_{2}) = s (c_{1} {\vec{v}}_{1} + c_{2} {\vec{v}}_{2}) = c_{1} s {\vec{v}}_{1} + c_{2} s {\vec{v}}_{2} = c_{1} \cdot d_{s} ({\vec{v}}_{1}) + c_{2} \cdot d_{s} ({\vec{v}}_{2})$
and therefore is an isomorphism.
As in the prior item, we can show that the map $t_{θ}$ is a correspondence by noting that it has an inverse, $t_{- θ}$ . That the map preserves structure is geometrically easy to see. For instance, adding two vectors and then rotating them has the same effect as rotating first and then adding. For an algebraic argument, consider polar coordinates: the map $t_{θ}$ sends the vector with endpoint $(r, ϕ)$ to the vector with endpoint $(r, ϕ + θ)$ . Then the familiar trigonometric formulas $\cos (ϕ + θ) = \cos ϕ \cos θ - \sin ϕ \sin θ$ and $\sin (ϕ + θ) = \sin ϕ \cos θ + \cos ϕ \sin θ$ show how to express the map's action in the usual rectangular coordinate system.
$(\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} r \cos ϕ \\ r \sin ϕ \end{matrix}) \overset{t_{θ}}{⟼} (\begin{matrix} r \cos (ϕ + θ) \\ r \sin (ϕ + θ) \end{matrix}) = (\begin{matrix} x \cos θ - y \sin θ \\ x \sin θ + y \cos θ \end{matrix})$
Now the calculation for preservation of addition is routine.
$(\begin{matrix} x_{1} + x_{2} \\ y_{1} + y_{2} \end{matrix}) \overset{t_{θ}}{⟼} (\begin{matrix} (x_{1} + x_{2}) \cos θ - (y_{1} + y_{2}) \sin θ \\ (x_{1} + x_{2}) \sin θ + (y_{1} + y_{2}) \cos θ \end{matrix}) = (\begin{matrix} x_{1} \cos θ - y_{1} \sin θ \\ x_{1} \sin θ + y_{1} \cos θ \end{matrix}) + (\begin{matrix} x_{2} \cos θ - y_{2} \sin θ \\ x_{2} \sin θ + y_{2} \cos θ \end{matrix})$
The calculation for preservation of scalar multiplication is similar.
This map is a correspondence because it has an inverse (namely, itself). As in the last item, that the reflection map preserves structure is geometrically easy to see: adding vectors and then reflecting gives the same result as reflecting first and then adding, for instance. For an algebraic proof, suppose that the line $ℓ$ has slope $k$ (the case of a line with undefined slope can be done as a separate, but easy, case). We can follow the hint and use polar coordinates: where the line $ℓ$ forms an angle of $ϕ$ with the $x$ -axis, the action of $f_{ℓ}$ is to send the vector with endpoint $(r \cos θ, r \sin θ)$ to the one with endpoint $(r \cos (2 ϕ - θ), r \sin (2 ϕ - θ))$ .

To convert to rectangular coordinates, we will use some trigonometric formulas, as we did in the prior item. First observe that $\cos ϕ$ and $\sin ϕ$ can be determined from the slope $k$ of the line. This picture

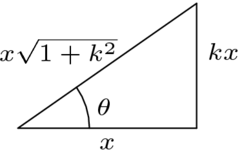
gives that $\cos ϕ = 1 / \sqrt{1 + k^{2}}$ and $\sin ϕ = k / \sqrt{1 + k^{2}}$ . Now,

$\begin{matrix} \cos (2 ϕ - θ) & = \cos (2 ϕ) \cos θ + \sin (2 ϕ) \sin θ \\ = (\cos^{2} ϕ - \sin^{2} ϕ) \cos θ + (2 \sin ϕ \cos ϕ) \sin θ \\ = ((\frac{1}{\sqrt{1 + k^{2}}})^{2} - (\frac{k}{\sqrt{1 + k^{2}}})^{2}) \cos θ + (2 \frac{k}{\sqrt{1 + k^{2}}} \frac{1}{\sqrt{1 + k^{2}}}) \sin θ \\ = (\frac{1 - k^{2}}{1 + k^{2}}) \cos θ + (\frac{2 k}{1 + k^{2}}) \sin θ \end{matrix}$

and thus the first component of the image vector is this.

$r \cdot \cos (2 ϕ - θ) = \frac{1 - k^{2}}{1 + k^{2}} \cdot x + \frac{2 k}{1 + k^{2}} \cdot y$

A similar calculation shows that the second component of the image vector is this.

$r \cdot \sin (2 ϕ - θ) = \frac{2 k}{1 + k^{2}} \cdot x - \frac{1 - k^{2}}{1 + k^{2}} \cdot y$

With this algebraic description of the action of $f_{ℓ}$

$(\begin{matrix} x \\ y \end{matrix}) \overset{f_{ℓ}}{⟼} (\begin{matrix} (1 - k^{2} / 1 + k^{2}) \cdot x + (2 k / 1 + k^{2}) \cdot y \\ (2 k / 1 + k^{2}) \cdot x - (1 - k^{2} / 1 + k^{2}) \cdot y \end{matrix})$

checking that it preserves structure is routine.

Problem 21

Produce an automorphism of $𝒫_{2}$ other than the identity map, and other than a shift map $p (x) \mapsto p (x - k)$ .

Answer

First, the map $p (x) \mapsto p (x + k)$ doesn't count because it is a version of $p (x) \mapsto p (x - k)$ . Here is a correct answer (many others are also correct): $a_{0} + a_{1} x + a_{2} x^{2} \mapsto a_{2} + a_{0} x + a_{1} x^{2}$ . Verification that this is an isomorphism is straightforward.

Problem 22

Show that a function $f : ℝ^{1} \to ℝ^{1}$ is an automorphism if and only if it has the form $x \mapsto k x$ for some $k \neq 0$ .
Let $f$ be an automorphism of $ℝ^{1}$ such that $f (3) = 7$ . Find $f (- 2)$ .
Show that a function $f : ℝ^{2} \to ℝ^{2}$ is an automorphism if and only if it has the form
$(\begin{matrix} x \\ y \end{matrix}) \mapsto (\begin{matrix} a x + b y \\ c x + d y \end{matrix})$
for some $a, b, c, d \in ℝ$ with $a d - b c \neq 0$ . Hint. Exercises in prior subsections have shown that
$(\begin{matrix} b \\ d \end{matrix}) is not a multiple of (\begin{matrix} a \\ c \end{matrix})$
if and only if $a d - b c \neq 0$ .
Let $f$ be an automorphism of $ℝ^{2}$ with
$f ((\begin{matrix} 1 \\ 3 \end{matrix})) = (\begin{matrix} 2 \\ - 1 \end{matrix}) and f ((\begin{matrix} 1 \\ 4 \end{matrix})) = (\begin{matrix} 0 \\ 1 \end{matrix}) .$
Find
$f ((\begin{matrix} 0 \\ - 1 \end{matrix})) .$

Answer

For the "only if" half, let $f : ℝ^{1} \to ℝ^{1}$ to be an isomorphism. Consider the basis $⟨ 1 ⟩ \subseteq ℝ^{1}$ . Designate $f (1)$ by $k$ . Then for any $x$ we have that $f (x) = f (x \cdot 1) = x \cdot f (1) = x k$ , and so $f$ 's action is multiplication by $k$ . To finish this half, just note that $k \neq 0$ or else $f$ would not be one-to-one. For the "if" half we only have to check that such a map is an isomorphism when $k \neq 0$ . To check that it is one-to-one, assume that $f (x_{1}) = f (x_{2})$ so that $k x_{1} = k x_{2}$ and divide by the nonzero factor $k$ to conclude that $x_{1} = x_{2}$ . To check that it is onto, note that any $y \in ℝ^{1}$ is the image of $x = y / k$ (again, $k \neq 0$ ). Finally, to check that such a map preserves combinations of two members of the domain, we have this.
$f (c_{1} x_{1} + c_{2} x_{2}) = k (c_{1} x_{1} + c_{2} x_{2}) = c_{1} k x_{1} + c_{2} k x_{2} = c_{1} f (x_{1}) + c_{2} f (x_{2})$
By the prior item, $f$ 's action is $x \mapsto (7 / 3) x$ . Thus $f (- 2) = - 14 / 3$ .
For the "only if" half, assume that $f : ℝ^{2} \to ℝ^{2}$ is an automorphism. Consider the standard basis $ℰ_{2}$ for $ℝ^{2}$ . Let
$f ({\vec{e}}_{1}) = (\begin{matrix} a \\ c \end{matrix}) and f ({\vec{e}}_{2}) = (\begin{matrix} b \\ d \end{matrix}) .$
Then the action of $f$ on any vector is determined by by its action on the two basis vectors.
$f ((\begin{matrix} x \\ y \end{matrix})) = f (x \cdot {\vec{e}}_{1} + y \cdot {\vec{e}}_{2}) = x \cdot f ({\vec{e}}_{1}) + y \cdot f ({\vec{e}}_{2}) = x \cdot (\begin{matrix} a \\ c \end{matrix}) + y \cdot (\begin{matrix} b \\ d \end{matrix}) = (\begin{matrix} a x + b y \\ c x + d y \end{matrix})$
To finish this half, note that if $a d - b c = 0$ , that is, if $f ({\vec{e}}_{2})$ is a multiple of $f ({\vec{e}}_{1})$ , then $f$ is not one-to-one. For "if" we must check that the map is an isomorphism, under the condition that $a d - b c \neq 0$ . The structure-preservation check is easy; we will here show that $f$ is a correspondence. For the argument that the map is one-to-one, assume this.
$f ((\begin{matrix} x_{1} \\ y_{1} \end{matrix})) = f ((\begin{matrix} x_{2} \\ y_{2} \end{matrix})) and so (\begin{matrix} a x_{1} + b y_{1} \\ c x_{1} + d y_{1} \end{matrix}) = (\begin{matrix} a x_{2} + b y_{2} \\ c x_{2} + d y_{2} \end{matrix})$
Then, because $a d - b c \neq 0$ , the resulting system
$\begin{matrix} a (x_{1} - x_{2}) & + & b (y_{1} - y_{2}) & = & 0 \\ c (x_{1} - x_{2}) & + & d (y_{1} - y_{2}) & = & 0 \end{matrix}$
has a unique solution, namely the trivial one $x_{1} - x_{2} = 0$ and $y_{1} - y_{2} = 0$ (this follows from the hint). The argument that this map is onto is closely related— this system
$\begin{matrix} a x_{1} & + & b y_{1} & = & x \\ c x_{1} & + & d y_{1} & = & y \end{matrix}$
has a solution for any $x$ and $y$ if and only if this set
${(\begin{matrix} a \\ c \end{matrix}), (\begin{matrix} b \\ d \end{matrix})}$
spans $ℝ^{2}$ , i.e., if and only if this set is a basis (because it is a two-element subset of $ℝ^{2}$ ), i.e., if and only if $a d - b c \neq 0$ .
$f ((\begin{matrix} 0 \\ - 1 \end{matrix})) = f ((\begin{matrix} 1 \\ 3 \end{matrix}) - (\begin{matrix} 1 \\ 4 \end{matrix})) = f ((\begin{matrix} 1 \\ 3 \end{matrix})) - f ((\begin{matrix} 1 \\ 4 \end{matrix})) = (\begin{matrix} 2 \\ - 1 \end{matrix}) - (\begin{matrix} 0 \\ 1 \end{matrix}) = (\begin{matrix} 2 \\ - 2 \end{matrix})$

Problem 23

Refer to Lemma 1.8 and Lemma 1.9. Find two more things preserved by isomorphism.

Answer

There are many answers; two are linear independence and subspaces.

To show that if a set ${{\vec{v}}_{1}, \dots, {\vec{v}}_{n}}$ is linearly independent then its image ${f ({\vec{v}}_{1}), \dots, f ({\vec{v}}_{n})}$ is also linearly independent, consider a linear relationship among members of the image set.

0 = c_{1} f ({\vec{v}}_{1}) + \dots + c_{n} f (\vec{v_{n}}) = f (c_{1} {\vec{v}}_{1}) + \dots + f (c_{n} \vec{v_{n}}) = f (c_{1} {\vec{v}}_{1} + \dots + c_{n} \vec{v_{n}})

Because this map is an isomorphism, it is one-to-one. So $f$ maps only one vector from the domain to the zero vector in the range, that is, $c_{1} {\vec{v}}_{1} + \dots + c_{n} {\vec{v}}_{n}$ equals the zero vector (in the domain, of course). But, if ${{\vec{v}}_{1}, \dots, {\vec{v}}_{n}}$ is linearly independent then all of the $c$ 's are zero, and so ${f ({\vec{v}}_{1}), \dots, f ({\vec{v}}_{n})}$ is linearly independent also. (Remark. There is a small point about this argument that is worth mention. In a set, repeats collapse, that is, strictly speaking, this is a one-element set: ${\vec{v}, \vec{v}}$ , because the things listed as in it are the same thing. Observe, however, the use of the subscript $n$ in the above argument. In moving from the domain set ${{\vec{v}}_{1}, \dots, {\vec{v}}_{n}}$ to the image set ${f ({\vec{v}}_{1}), \dots, f ({\vec{v}}_{n})}$ , there is no collapsing, because the image set does not have repeats, because the isomorphism $f$ is one-to-one.)

To show that if $f : V \to W$ is an isomorphism and if $U$ is a subspace of the domain $V$ then the set of image vectors $f (U) = {\vec{w} \in W | \vec{w} = f (\vec{u}) for some \vec{u} \in U}$ is a subspace of $W$ , we need only show that it is closed under linear combinations of two of its members (it is nonempty because it contains the image of the zero vector). We have

c_{1} \cdot f ({\vec{u}}_{1}) + c_{2} \cdot f ({\vec{u}}_{2}) = f (c_{1} {\vec{u}}_{1}) + f (c_{2} {\vec{u}}_{2}) = f (c_{1} {\vec{u}}_{1} + c_{2} {\vec{u}}_{2})

and $c_{1} {\vec{u}}_{1} + c_{2} {\vec{u}}_{2}$ is a member of $U$ because of the closure of a subspace under combinations. Hence the combination of $f ({\vec{u}}_{1})$ and $f ({\vec{u}}_{2})$ is a member of $f (U)$ .

Problem 24

We show that isomorphisms can be tailored to fit in that, sometimes, given vectors in the domain and in the range we can produce an isomorphism associating those vectors.

Let $B = ⟨ {\vec{β}}_{1}, {\vec{β}}_{2}, {\vec{β}}_{3} ⟩$ be a basis for $𝒫_{2}$ so that any $\vec{p} \in 𝒫_{2}$ has a unique representation as $\vec{p} = c_{1} {\vec{β}}_{1} + c_{2} {\vec{β}}_{2} + c_{3} {\vec{β}}_{3}$ , which we denote in this way.
${R e p}_{B} (\vec{p}) = (\begin{matrix} c_{1} \\ c_{2} \\ c_{3} \end{matrix})$
Show that the ${R e p}_{B} (\cdot)$ operation is a function from $𝒫_{2}$ to $ℝ^{3}$ (this entails showing that with every domain vector $\vec{v} \in 𝒫_{2}$ there is an associated image vector in $ℝ^{3}$ , and further, that with every domain vector $\vec{v} \in 𝒫_{2}$ there is at most one associated image vector).
Show that this ${R e p}_{B} (\cdot)$ function is one-to-one and onto.
Show that it preserves structure.
Produce an isomorphism from $𝒫_{2}$ to $ℝ^{3}$ that fits these specifications.
$x + x^{2} \mapsto (\begin{matrix} 1 \\ 0 \\ 0 \end{matrix}) and 1 - x \mapsto (\begin{matrix} 0 \\ 1 \\ 0 \end{matrix})$

Answer

The association
$\vec{p} = c_{1} {\vec{β}}_{1} + c_{2} {\vec{β}}_{2} + c_{3} {\vec{β}}_{3} \overset{{R e p}_{B} (\cdot)}{⟼} (\begin{matrix} c_{1} \\ c_{2} \\ c_{3} \end{matrix})$
is a function if every member $\vec{p}$ of the domain is associated with at least one member of the codomain, and if every member $\vec{p}$ of the domain is associated with at most one member of the codomain. The first condition holds because the basis $B$ spans the domain— every $\vec{p}$ can be written as at least one linear combination of $\vec{β}$ 's. The second condition holds because the basis $B$ is linearly independent— every member $\vec{p}$ of the domain can be written as at most one linear combination of the $\vec{β}$ 's.
For the one-to-one argument, if ${R e p}_{B} (\vec{p}) = {R e p}_{B} (\vec{q})$ , that is, if ${R e p}_{B} (p_{1} {\vec{β}}_{1} + p_{2} {\vec{β}}_{2} + p_{3} {\vec{β}}_{3}) = {R e p}_{B} (q_{1} {\vec{β}}_{1} + q_{2} {\vec{β}}_{2} + q_{3} {\vec{β}}_{3})$ then
$(\begin{matrix} p_{1} \\ p_{2} \\ p_{3} \end{matrix}) = (\begin{matrix} q_{1} \\ q_{2} \\ q_{3} \end{matrix})$
and so $p_{1} = q_{1}$ and $p_{2} = q_{2}$ and $p_{3} = q_{3}$ , which gives the conclusion that $\vec{p} = \vec{q}$ . Therefore this map is one-to-one. For onto, we can just note that
$(\begin{matrix} a \\ b \\ c \end{matrix})$
equals ${R e p}_{B} (a {\vec{β}}_{1} + b {\vec{β}}_{2} + c {\vec{β}}_{3})$ , and so any member of the codomain $ℝ^{3}$ is the image of some member of the domain $𝒫_{2}$ .
This map respects addition and scalar multiplication because it respects combinations of two members of the domain (that is, we are using item 2 of Lemma 1.9): where $\vec{p} = p_{1} {\vec{β}}_{1} + p_{2} {\vec{β}}_{2} + p_{3} {\vec{β}}_{3}$ and $\vec{q} = q_{1} {\vec{β}}_{1} + q_{2} {\vec{β}}_{2} + q_{3} {\vec{β}}_{3}$ , we have this.
$\begin{matrix} {R e p}_{B} (c \cdot \vec{p} + d \cdot \vec{q}) & = {R e p}_{B} ((c p_{1} + d q_{1}) {\vec{β}}_{1} + (c p_{2} + d q_{2}) {\vec{β}}_{2} + (c p_{3} + d q_{3}) {\vec{β}}_{3}) \\ = (\begin{matrix} c p_{1} + d q_{1} \\ c p_{2} + d q_{2} \\ c p_{3} + d q_{3} \end{matrix}) \\ = c \cdot (\begin{matrix} p_{1} \\ p_{2} \\ p_{3} \end{matrix}) + d \cdot (\begin{matrix} q_{1} \\ q_{2} \\ q_{3} \end{matrix}) \\ = {R e p}_{B} (\vec{p}) + {R e p}_{B} (\vec{q}) \end{matrix}$
Use any basis $B$ for $𝒫_{2}$ whose first two members are $x + x^{2}$ and $1 - x$ , say $B = ⟨ x + x^{2}, 1 - x, 1 ⟩$ .

Problem 25

Prove that a space is $n$ -dimensional if and only if it is isomorphic to $ℝ^{n}$ . Hint. Fix a basis $B$ for the space and consider the map sending a vector over to its representation with respect to $B$ .

Answer

See the next subsection.

Problem 26

(Requires the subsection on Combining Subspaces, which is optional.) Let $U$ and $W$ be vector spaces. Define a new vector space, consisting of the set $U \times W = {(\vec{u}, \vec{w}) | \vec{u} \in U and \vec{w} \in W}$ along with these operations.

({\vec{u}}_{1}, {\vec{w}}_{1}) + ({\vec{u}}_{2}, {\vec{w}}_{2}) = ({\vec{u}}_{1} + {\vec{u}}_{2}, {\vec{w}}_{1} + {\vec{w}}_{2}) and r \cdot (\vec{u}, \vec{w}) = (r \vec{u}, r \vec{w})

This is a vector space, the external direct sum of $U$ and $W$ .

Check that it is a vector space.
Find a basis for, and the dimension of, the external direct sum $𝒫_{2} \times ℝ^{2}$ .
What is the relationship among $\dim (U)$ , $\dim (W)$ , and $\dim (U \times W)$ ?
Suppose that $U$ and $W$ are subspaces of a vector space $V$ such that $V = U \oplus W$ (in this case we say that $V$ is the internal direct sum of $U$ and $W$ ). Show that the map $f : U \times W \to V$ given by
$(\vec{u}, \vec{w}) \overset{f}{⟼} \vec{u} + \vec{w}$
is an isomorphism. Thus if the internal direct sum is defined then the internal and external direct sums are isomorphic.

Answer

Most of the conditions in the definition of a vector space are routine. We here sketch the verification of part 1 of that definition. For closure of $U \times W$ , note that because $U$ and $W$ are closed, we have that ${\vec{u}}_{1} + {\vec{u}}_{2} \in U$ and ${\vec{w}}_{1} + {\vec{w}}_{2} \in W$ and so $({\vec{u}}_{1} + {\vec{u}}_{2}, {\vec{w}}_{1} + {\vec{w}}_{2}) \in U \times W$ . Commutativity of addition in $U \times W$ follows from commutativity of addition in $U$ and $W$ .
$({\vec{u}}_{1}, {\vec{w}}_{1}) + ({\vec{u}}_{2}, {\vec{w}}_{2}) = ({\vec{u}}_{1} + {\vec{u}}_{2}, {\vec{w}}_{1} + {\vec{w}}_{2}) = ({\vec{u}}_{2} + {\vec{u}}_{1}, {\vec{w}}_{2} + {\vec{w}}_{1}) = ({\vec{u}}_{2}, {\vec{w}}_{2}) + ({\vec{u}}_{1}, {\vec{w}}_{1})$
The check for associativity of addition is similar. The zero element is $({\vec{0}}_{U}, {\vec{0}}_{W}) \in U \times W$ and the additive inverse of $(\vec{u}, \vec{w})$ is $(- \vec{u}, - \vec{w})$ . The checks for the second part of the definition of a vector space are also straightforward.
This is a basis
$⟨ (1, (\begin{matrix} 0 \\ 0 \end{matrix})), (x, (\begin{matrix} 0 \\ 0 \end{matrix})), (x^{2}, (\begin{matrix} 0 \\ 0 \end{matrix})), (1, (\begin{matrix} 1 \\ 0 \end{matrix})), (1, (\begin{matrix} 0 \\ 1 \end{matrix})) ⟩$
because there is one and only one way to represent any member of $𝒫_{2} \times ℝ^{2}$ with respect to this set; here is an example.
$(3 + 2 x + x^{2}, (\begin{matrix} 5 \\ 4 \end{matrix})) = 3 \cdot (1, (\begin{matrix} 0 \\ 0 \end{matrix})) + 2 \cdot (x, (\begin{matrix} 0 \\ 0 \end{matrix})) + (x^{2}, (\begin{matrix} 0 \\ 0 \end{matrix})) + 5 \cdot (1, (\begin{matrix} 1 \\ 0 \end{matrix})) + 4 \cdot (1, (\begin{matrix} 0 \\ 1 \end{matrix}))$
The dimension of this space is five.
We have $\dim (U \times W) = \dim (U) + \dim (W)$ as this is a basis.
$⟨ ({\vec{μ}}_{1}, {\vec{0}}_{W}), \dots, ({\vec{μ}}_{\dim (U)}, {\vec{0}}_{W}), ({\vec{0}}_{U}, {\vec{ω}}_{1}), \dots, ({\vec{0}}_{U}, {\vec{ω}}_{\dim (W)}) ⟩$
We know that if $V = U \oplus W$ then each $\vec{v} \in V$ can be written as $\vec{v} = \vec{u} + \vec{w}$ in one and only one way. This is just what we need to prove that the given function an isomorphism. First, to show that $f$ is one-to-one we can show that if $f (({\vec{u}}_{1}, {\vec{w}}_{1})) = (({\vec{u}}_{2}, {\vec{w}}_{2}))$ , that is, if ${\vec{u}}_{1} + {\vec{w}}_{1} = {\vec{u}}_{2} + {\vec{w}}_{2}$ then ${\vec{u}}_{1} = {\vec{u}}_{2}$ and ${\vec{w}}_{1} = {\vec{w}}_{2}$ . But the statement "each $\vec{v}$ is such a sum in only one way" is exactly what is needed to make this conclusion. Similarly, the argument that $f$ is onto is completed by the statement that "each $\vec{v}$ is such a sum in at least one way". This map also preserves linear combinations
$\begin{matrix} f (c_{1} \cdot ({\vec{u}}_{1}, {\vec{w}}_{1}) + c_{2} \cdot ({\vec{u}}_{2}, {\vec{w}}_{2})) & = f ((c_{1} {\vec{u}}_{1} + c_{2} {\vec{u}}_{2}, c_{1} {\vec{w}}_{1} + c_{2} {\vec{w}}_{2})) \\ = c_{1} {\vec{u}}_{1} + c_{2} {\vec{u}}_{2} + c_{1} {\vec{w}}_{1} + c_{2} {\vec{w}}_{2} \\ = c_{1} {\vec{u}}_{1} + c_{1} {\vec{w}}_{1} + c_{2} {\vec{u}}_{2} + c_{2} {\vec{w}}_{2} \\ = c_{1} \cdot f (({\vec{u}}_{1}, {\vec{w}}_{1})) + c_{2} \cdot f (({\vec{u}}_{2}, {\vec{w}}_{2})) \end{matrix}$
and so it is an isomorphism.