Introduction to Inorganic Chemistry/Review of Chemical Bonding
Chapter 1: Review of Chemical Bonding
[edit | edit source]
Molecules (and extended solids) are built from atoms that form chemical bonds. Theories of bonding seek to explain why molecules and solids form, what their structures are, why some are more stable than others, and how they react. As we will learn in Chapter 2, quantum mechanics gives us the most realistic picture of chemical bonding via molecular orbital (MO) theory. However, the MO description of bonding is conceptually difficult and mathematically intensive. This chapter will review less rigorous (but still useful) models such as Lewis dot structures and valence shell electron-pair repulsion (VSEPR) theory. When combined with a qualitative quantum mechanical description of bonding through the concepts of orbital hybridization and resonance, these simple models can help us understand a great deal about the structures, stabilities, and reactions of inorganic molecules.
The theory of chemical bonding has a long history, dating back to ancient Greece and the atomists Democritus, Leucippus, and the Epicureans. They postulated the existence of immutable atoms moving through the void, and envisioned the physical properties of materials as arising from the kinds and shapes of atoms. In his epic poem De rerum natura (On the Nature of Things), the Roman poet Lucretius (c. 99 BC – c. 50 BC), drawing on his Epicurean beliefs, describes some atoms and chemical bonding in the following way:
What seems to us the hardened and condensed
Must be of atoms among themselves more hooked,
Be held compacted deep within, as 'twere
By branch-like atoms -- of which sort the chief
Are diamond stones, despisers of all blows
And stalwart flint and strength of solid iron
And brazen bars, which, budging hard in locks,
Do grate and scream. But what are liquid, formed
Of fluid body, they indeed must be
Of elements more smooth and round -- because
Their globules severally will not cohere.
Lucretius' poem is enjoyable reading and contains some remarkable insights into the microscopic world, given the tools available at the time. Modern analytical methods show that he was off base with his ideas about hooks and spheres, however. We will revisit the nature of chemical bonding in the substances Lucretius mentions (diamond, silicates, iron, brass, and water) in the context of modern chemical theories to understand why they have the special properties they do.
Learning goals for Chapter 1:
- Be able to draw Lewis dot structures, assign formal charges, predict molecular geometries (including bond angles), and calculate bond orders for molecules, including hypervalent molecules and ions.
- Describe hypervalent molecules using no-bond resonance.
- Understand and articulate how predictions of molecular structure and bonding can be experimentally verified.
- Learn to construct hybrid orbitals from s and p atomic orbitals.
- Use the isoelectronic principle to design new molecules and solids.
- Rationalize bond strength and chemical reactivity using bond polarity arguments.
- Interrelate bond length and bond strength.
1.1 Valence bond theory: Lewis dot structures, the octet rule, formal charge, resonance, and the isoelectronic principle
[edit | edit source]
Atoms and Molecules
Atomism, because it was dismissed by Aristotle, enjoyed a long sleep in scientific discourse until it was reconsidered by Galileo, Decartes, and Gassendi in the 1600s. Dalton postulated the modern atomic theory in 1808 based on his observation that elements such as hydrogen and oxygen combined in specific ratios (the Law of Definite Proportions), but the atomic theory remained contentious throughout most of the 19th century. Thompson, Rutherford, Bohr, and others around the turn of the 20th century established that matter was indeed composed of atoms that contained heavy nuclei and light electrons, and that atoms could exist in excited states that could be interpreted as excitations of their electrons to different energy levels. However the atomic theory did not provide a ready explanation for the bonded states of atoms in molecules.
In 1916, still more than a decade before modern quantum theory would adequately describe the shapes of atomic orbitals, Lewis proposed the octet theory based on the empirically observed rules of valence, i.e., the combining ratios of atoms in molecules.[1] This theory, in hindsight, can be rationalized for s- and p-block elements by observing that main-group atoms can use their four valence orbitals (s, px, py, and pz) to accommodate up to eight electrons, some or all of which may be shared with other atoms. In Lewis' model, the valence electrons of an atom were situated at the corners of a cube, and the cubes could share edges or faces to complete their octets. Lewis developed a shorthand notation for these structures based on dots that represented the valence electrons, as illustrated in Fig. 1.1.1. A pair of electrons shared between atoms constitutes a chemical bond, and can also be represented as a line joining the atoms. Four electrons shared between atoms, represented by two lines, is a double bond, and so forth. Any pairs of electrons not involved in bonding form "lone pairs" that belong to one atom only and are thus not involved in bonding.
The Lewis picture is powerful in its simplicity. It can be readily used to rationalize or predict the combining ratios of atoms, to sort plausible and unlikely structures for molecules (including large ones), and to rationalize the acid-base properties of many molecules. It is important to remember that the model is built on a shaky, pre-quantum mechanical description of atoms and so with it, we will make mistakes. Nevertheless it is useful to see how far we can go with the Lewis model.
Constructing the octet valence bond picture for a molecule
We can construct an octet picture for any molecule using the N-V method:
- Number of electrons needed to make separate octets around all atoms = N
- (N = 8 for non-H atoms, N = 2 for H)
- Number of valence electrons = V (add up using group numbers; don't forget to add or subtract for charges on ions)
- Number of shared electrons = S = N-V; and therefore the number of bonds = S/2
- Fill in lone pairs everywhere else to complete octets
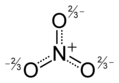
Example: nitrate anion, NO3-
- N = 4 atoms x 8 electrons = 32
- V = 5 + 6 + 6 + 6 + 1 = 24 (N + O + O + O + charge)
- S = 32-24 = 8 shared electrons = 4 bonds
- The number of lone pairs is obtained by difference: (V-S)/2 = (24-8)/2 = 8
- Now draw the molecule, starting with the four bonds and adding eight lone pairs to complete the octets:
- Count the shared and unshared electrons around each atom in the nitrate ion and you will see that all atoms are octet and that the total number of valence electrons (V) is 24. If you do the N-V calculation according to the rules above, you should always get an octet structure.

The formal charge distribution is assigned by dividing the shared (bonding) electrons equally between atoms. Thus, the singly bonded O atoms each possess 7 electrons, and because O is in group 6, their formal charge is -1. The doubly bonded O has a formal charge of zero. The N atom has a formal charge of +1 because it "owns" 4 valence electrons and is in group 5.
Note that the formal charge is not the same thing as the oxidation number (or oxidation state). In the nitrate ion, the oxidation state of nitrogen is +5 and the oxidation state of oxygen is -2. The formal charge is typically closer to the "real" charge on the atom (as measured, e.g., by X-ray photoelectron spectroscopy). Oxidation states are a useful bookkeeping device for keeping track of oxidation-reduction reactions, as we will discuss in Chapter 4. Like oxidation states, the formal charges on the atoms in a molecule or ion must add up to its overall charge.
We can similarly draw the Lewis structure for ammonia as shown below:
When we divide the shared electrons equally between the atoms, we see that the N atom has five electrons and each H atom has one. These are the same as their group numbers, and thus, all the formal charges in the ammonia molecule are zero.
Octet structures of the Lewis acid-base adduct NH3BF3, the hydronium ion H3O+, and the sulfate anion SO42- are shown below. In this case (and in many Lewis structures we will draw), we leave off the implied lone pairs around the peripheral atoms. Try calculating the number of bonds in each of these molecules using the N-V method, and fill in the lone pairs that are not explicitly drawn in.
In cases where more than one valence bond structure is possible, we can use formal charges to decide which structures should be more or less stable. The rules are:
- The formal charges on atoms are minimized in stable structures, zero being the best case.
- Negative formal charges should be placed on the most electronegative atom(s).
- Positive formal charges should be placed on the least electronegative atom(s).
- It is unfavorable to place like charges (++ or --) on neighboring atoms in a molecule.
Examples of these rules are shown below for alternative structures of BF3 and ONF.


Life outside of the ocean owes its existence to the presence of ozone (O3) in the stratosphere. Ozone absorbs the ultraviolet light in the solar spectrum, which otherwise would cause catastrophic damage to DNA and other biological molecules. Because ozone is produced photochemically from O2, which is itself generated by photosynthesis, the spectroscopic signature of ozone in the atmosphere of distant planets is one possible way to look for extraterrestrial life. 
Susan Solomon discovered the heterogeneous catalytic mechanism whereby ozone is decomposed by chlorofluorocarbons (freons), creating the Antarctic ozone hole. Her work formed the basis of the U.N. Montreal Protocol, an international agreement to protect the ozone layer by regulating damaging chemicals.
In the BF3 case, the structure on the left is non-octet, because there are only six electrons (three bonds) in the valence shell of B. Such structures are said to be electron deficient. An octet structure (right) can be drawn, but it places a positive formal charge on F, the most electronegative atom in the molecule. Thus, neither structure is completely "happy," but the formal charge rules tell us that the electron-deficient structure on the left is more stable. The electron deficiency of BF3 makes it a powerful Lewis acid.
In the case of ONF, the structure on the left is unfavorable for two reasons. First, it places a positive formal charge on F, the most electronegative atom. Second, there is another possible structure (right) that has zero formal charge, which is preferable to one with non-zero charge. This means that the structure on the right, with a double bond between N and O, is more reasonable.
Resonance structures
The ozone (O3) molecule has two equivalent octet structures, shown below:
In both cases, the Lewis dot diagram suggests that there are three kinds of oxygen atoms in the molecule, with +1, 0, and -1 formal charges. These structures also suggest that ozone should have one single and one double bond. Experimentally (by electron diffraction), however, we find that the molecule is symmetric, with both O-O bond lengths the same. The real (instantaneous) structure is the average of the two forms, as shown below. In the classical Lewis picture of the molecule, we can rationalize resonance by observing that electrons, being thousands of times lighter than the nuclei of atoms, move very fast on the timescale of molecular vibrations. Thus, in the time it takes for the oxygen atoms to adjust their positions, the electrons can move back and forth many times. In the quantum mechanical MO picture (Chapter 2), we will see that resonance involves electrons that are fully delocalized over the atoms in the molecule. We represent resonance structures with a double-headed arrow to signify that the only difference between the Lewis structures is the distribution of electrons.
In the instantaneous structure of ozone, the formal (-) charge is shared between the two terminal oxygen atoms and therefore each one has a formal charge of -1/2. The O-O bonds are the average of a single and a double bond, i.e., each O-O bond order is 1.5.

Similarly, the nitrate anion has three resonance structures, and experimentally (by X-ray crystallography of nitrate salts) we find that all the N-O bonds in the ion are the same. In this case, in the averaged structure, each O atom has a formal charge of -2/3 and the N-O bond order is 4/3 (=1.33...).

Inequivalent resonance structures
The rules of resonance also apply to inequivalent structures, which in general will have different energies from each other. In this case the structure of the molecule represents a weighted average of the low energy structures. A good example is the cyanate ion, OCN-. We can write three inequivalent octet structures for the molecule:
The first two are reasonable resonance structures, although we suspect the one on the left is the best because it puts the negative formal charge on the most electronegative atom. The last one is clearly a bad resonance structure, because the formal charges are high and there is a positive charge on the oxygen atom. The real structure is thus a weighted average of the first two.
No-bond resonance
An interesting and useful kind of inequivalent resonance structure is one in which there is a bond order of zero between two of the atoms. This concept of no-bond resonance is important in understanding the bonding in many halogen- and hydrogen-containing compounds. The idea is illustrated below for the generic molecule X-Y-Z, where Z might be an electronegative halogen atom such as F. By moving the bonding electrons from the Y-Z bond onto the Z atom, and moving a lone pair from X into the X-Y bond, we generate the resonance structure shown on the right in which all atoms remain octet, but there is no bond between Y and Z.

It is important to recognize in this example that the no-bond form is only one resonance structure, and therefore the Z atom is still bound to Y. If the two resonance structures in this example have the same energy, we would expect the X-Y bond order to be 1.5 and the Y-Z bond order to be 0.5. Therefore the Y-Z bond should be longer than it is in a compound where the bond order is one, and it should be relatively easy to break the Y-Z bond.
Some molecular examples of no-bond resonance are shown below. In the molecule ONF3, the N-F bond is unusually long relative to the N-F bond in NF3, in which the bond order is 1. This can be explained by the no-bond resonance forms shown on the right. Similarly, in the Lewis acid-base adduct formed by combining BH3 with CO, we can explain the long B-H bonds using no-bond resonance forms that place a partial positive charge on the H atoms.

No-bond resonance is often used to provide an octet bonding picture for so-called hypervalent compounds, which are compounds that appear to have more than 8 valence electrons in the bonding shell of the central atom. For example, we can consider two different valence bond structures for the triiodide ion, I3-, which is formed by reaction of I- with I2 in water:


In this structure, the central iodine atom has 10 electrons in its valence shell, in violation of the octet rule. Raman spectra of the triiodide ion show that the I-I bond is weaker than the I-I single bond in I2, suggesting that this picture is not an accurate description of the bonding. A better representation of I3- can be obtained with no-bond resonance structures, as shown below. We will see that this picture is consistent with the MO description of I3- in Chapter 2:
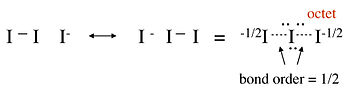

We can draw a similar picture for the XeF2 molecule, which has the same number of valence electrons as I3-. This picture is consistent with XPS data, which show a partial negative charge on the F atoms, as well as vibrational spectra, which show that the Xe-F bond is weaker in XeF2 than it is in the singly-bonded cation Xe-F+.

Other well known examples of hypervalent compounds are PF5, P(CH3)5, and SF6, as well as oxyacids such as H2SO4 and HClO4. The hypervalent structure is often drawn for these molecules, with the explanation that d-orbitals on the central atom contribute to the bonding in dsp3 and d2sp3 hybrids for 5- and 6-coordinate molecules, respectively. However, realistic molecular orbital calculations show that the phosphorus and sulfur 3d orbitals are too high in energy to contribute significantly to bonding in PF5 and SF6. For these molecules, we can use no-bond resonance to make reasonable octet structures that predict polar bonds between the central atom and F.


In other cases, such as P(CH3)5, the octet structure is unreasonable because it suggests a polar bond between P and C, with a partial negative charge on C. Further, in the case of oxyacids such as H2SO4 and HClO4, X-ray crystallographic data establish that the S-O and Cl-O bonds are shorter for the oxygen atoms not bonded to hydrogen, which is more consistent with the hypervalent picture:

The question of whether hypervalency and the octet rule are really useful descriptions of the bonding in these compounds has been considered in a number of computational studies, which have used increasingly accurate quantum mechanical calculations to determine the number of electrons associated with the central atom. In a 2002 study, Gillespie and Silvi[4] found that the population of the valence shell is greater than eight for compounds with electropositive ligands, such as P(CH3)5, and less than eight for compounds such as PF5. They concluded that these valence electron shell populations depend primarily on the coordination numbers and electronegativities of the central atoms and their ligands, and that there is no fundamental difference between the bonding in hypervalent and non-hypervalent (Lewis octet) molecules. This reminds us that the octet rule is not a law of nature, but rather an empirical rule that is useful within certain limits.

The isoelectronic principle
In calculating the octet structures of molecules using the N-V method, we needed to know only the number of atoms and the number of electrons, not the identities of the atoms themselves. This means that we will get the same answer (and the same set of octet and resonance structures) for any molecule or ion that contains (a) the same number of non-hydrogen atoms, and (b) the same total number of valence electrons. Such molecules are said to be isoelectronic. This is a powerful conclusion because, once we have determined the electronic structure of one molecule, we can write down the same solution for all other molecules that are isoelectronic. For example, we noted above that I3- and XeF2, which both have 22 valence electrons, have the same valence bond structure. We can further expect that isoelectronic molecules will have the same shapes and, very often, similar physical properties.
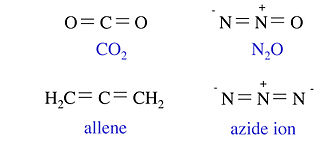
The four molecules and ions below all contain three non-hydrogen atoms and 16 valence electrons. All of them are linear molecules with two double bonds. The four molecules and ions shown below them all contain four non-hydrogen atoms and 24 valence electrons. These four have a trigonal planar shape. While BF3 is a member of this isoelectronic series, we do not write it in the resonance form that contains a B=F double bond, because that would put a positive formal charge on F.

Similarly we can show that CH4, NH3, NH4+, H2O, H3O+, HF, F-, and OH- are all isoelectronic with one non-H atom and eight valence electrons. In the next section we will see that this gives rise to nearly identical electronic shapes for these molecules.

Isoelectronic solids. The isoelectronic principle works not just for molecules but for extended solids as well. One technologically important set of isoelectronic solids are the p-block semiconductors. The group 14 element Si is the most widely used semiconductor for electronics, but, as we will discuss later, it is not a good light emitter. Light-emitting diodes (LEDs), which are used in lasers, high efficiency lighting, and display technologies, are made from compounds that are isoelectronic with Si and Ge, especially GaAs, GaP, AlAs, and GaN (all contain four valence electrons per atom). CdTe and CuIn1-xGaxSe2 (CIGS) are promising solar cell materials that also have the same number of valence electrons per atom. Like Si and Ge, these compounds have tetrahedrally bonded structures in the solid state and absorb light across most of the solar spectrum, as we will discuss in more detail in Chapters 8 and 10.
The isoelectronic principle is also a powerful tool in materials research, because it provides guidance about where to look for new materials with similar and perhaps improved properties. For example, the discovery that 8.5% efficient thin layer solar cells could be made with the compound CsSnI3[5] stimulated the exploration of many isoelectronic ABX3 compounds with the same perovskite crystal structure. Very recently thin film solar cells based on light absorbers in this structural family (MA)PbI3-xClx and FAxMA1−xPbBryI3−y (MA+ = methylammonium, CH3NH3+; FA+ = formamidinium, HC(NH2)2+) have been reported with efficiencies as high as 22%.[6][7][8]
1.2 The shapes of molecules (VSEPR theory) and orbital hybridization
[edit | edit source]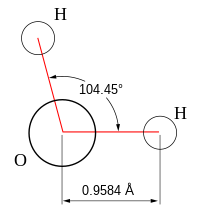
The Valence Shell Electron Pair Repulsion (VSEPR) theory is a simple and useful way to predict and rationalize the shapes of molecules. The theory is based on the idea of minimizing the electrostatic repulsion between electron pairs, as first proposed by Sidgwick and Powell in 1940,[9] then generalized by Gillespie and Nyholm in 1957,[10] and then broadly applied over the intervening 50+ years.[11]
To use the VSEPR model, one begins with the Lewis dot picture to determine the number of lone pairs and bonding domains around a central atom. Because VSEPR considers all bonding domains equally (i.e., a single bond, a double bond, and a half bond all count as one electron domain), one can use either an octet or hypervalent structure, provided that the number of lone pairs (which should be the same in both) is calculated correctly. For example, in either the hypervalent or octet structure of the I3- ion above, there are three lone pairs on the central I atom and two bonding domains. We then follow these steps to obtain the electronic geometry:
- Determine the number of lone pairs on the central atom in the molecule, and add the number of bonded atoms (a.k.a. bonding domains)
- This number (the steric number) defines the electronic shape of the molecule by minimizing repulsion. For example a steric number of three gives a trigonal planar electronic shape.
- The angles between electron domains are determined primarily by the electronic geometry (e.g., 109.5° for a steric number of 4, which implies that the electronic shape is a tetrahedron)
- These angles are adjusted by the hierarchy of repulsions: (lone pair - lone pair) > (lone pair - bond) > (bond - bond)
The molecular geometry is deduced from the electronic geometry by considering the lone pairs to be present but invisible. The most commonly used methods to determine molecular structure - X-ray diffraction, neutron diffraction, and electron diffraction - have a hard time seeing lone pairs, but they can accurately determine the lengths of bonds between atoms and the bond angles.
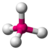
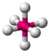
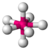
The table below gives examples of electronic and molecular shapes for steric numbers between 2 and 9. We are most often concerned with molecules that have steric numbers between 2 and 6.
| Bonding electron pairs | Lone pairs | Electron domains (Steric #) | Shape | Ideal bond angle (example's bond angle) | Example | Image |
|---|---|---|---|---|---|---|
2
|
0
|
2
|
180°
|
|||
3
|
0
|
3
|
120°
|
|||
2
|
1
|
3
|
120° (119°)
|
|||
4
|
0
|
4
|
109.5°
|
|||
3
|
1
|
4
|
109.5° (107°)
|
|||
2
|
2
|
4
|
109.5° (104.5°)
|
|||
5
|
0
|
5
|
90°, 120°, 180°
|
|||
4
|
1
|
5
|
180°, 120°, 90° (173.1°, 101.6°)
|
|||
3
|
2
|
5
|
90°, 180° (87.5°, < 180°)
|
|||
2
|
3
|
5
|
180°
|
|||
6
|
0
|
6
|
90°, 180°
|
|||
5
|
1
|
6
|
90° (84.8°), 180°
|
|||
4
|
2
|
6
|
90°, 180°
|
|||
7
|
0
|
7
|
90°, 72°, 180°
|
|||
6
|
1
|
7
|
72°, 90°, 144°
|
XeOF5−
|
||
5
|
2
|
7
|
72°, 144°
|
|||
8
|
0
|
8
|
||||
9
|
0
|
9
|
From the Table, we see that some of the molecules shown as examples have bond angles that depart from the ideal electronic geometry. For example, the H-N-H bond angle in ammonia is 107°, and the H-O-H angle in water is 104.5°. We can rationalize this in terms of the last rule above. The lone pair in ammonia repels the electrons in the N-H bonds more than the bonds repel each other. This lone pair repulsion exerts even more steric influence in the case of water, where there are two lone pairs. Similarly, the axial F-S-F angle in the "seesaw" molecule SF4 is a few degrees less than 180° because of repulsion by the lone pair in the molecule.
Geometrical isomers
For some molecules in the Table, we note that there is more than one possible shape that would satisfy the VSEPR rules. For example, the XeF2 molecule has a steric number of five and a trigonal bipyramidal geometry. There are three possible stereoisomers: one in which the F atoms occupy axial sites, resulting in linear molecule, one in which the F atoms occupy one equatorial and one axial site (resulting in a 90° bond angle), and one in which the F atoms are both on equatorial sites, with a F-Xe-F bond angle of 120°.

The observed geometry of XeF2 is linear, which can be rationalized by considering the orbitals that are used to make bonds (or lone pairs) in the axial and equatorial positions. There are four available orbitals, s, px, py, and pz. If we choose the z-axis as the axial direction, we can see that the px and py orbitals lie in the equatorial plane. We assume that the spherical s orbital is shared equally by the five electron domains in the molecule, the two axial bonds share the pz orbital, and the three equatorial bonds share the px and py orbitals. We can then calculate the bond orders to axial and equatorial F atoms as follows:
axial: 1/5 s + 1/2 pz = 0.7 bond (formal charge = -0.3)
equatorial: 1/5 s + 1/3 px + 1/3 py = 0.867 bond (formal charge = -0.133)
Because fluorine is more electronegative than a lone pair, it prefers the axial site where it will have more negative formal charge. In general, by this reasoning, lone pairs and electropositive ligands such as CH3 will always prefer the equatorial sites in the trigonal bipyramidal geometry. Electronegative ligands such as F will always go to the axial sites.
In the case of the BrF4- anion, which is isoelectronic with XeF4 in the Table, the electronic geometry is octahedral and there are two possible isomers in which the two lone pairs are cis or trans to each other. In this case, lone pair - lone pair repulsion dominates and we obtain the trans arrangement of lone pairs, giving a square planar molecular geometry.

Orbital hybridization
The observation of molecules in the various electronic shapes shown above is, at first blush, in conflict with our picture of atomic orbitals. For an atom such as oxygen, we know that the 2s orbital is spherical, and that the 2px, 2py, and 2pz orbitals are dumbell-shaped and point along the Cartesian axes. The water molecule contains two hydrogen atoms bound to oxygen not at a 90° angle, but at an angle of 104.5°. Given the relative orientations of the atomic orbitals, how do we arrive at angles between electron domains of 104.5°, 120°, and so on? To understand this we will need to learn a little bit about the quantum mechanics of electrons in atoms and molecules.
The atomic orbitals ψ represent solutions to the Schrödinger wave equation,
Here E is the energy of an electron in the orbital, and is the Hamiltonian operator.
By analogy with classical mechanics, the Hamiltonian is commonly expressed as the sum of operators corresponding to the kinetic and potential energies of a system in the form
where is the potential energy, and
is the kinetic energy operator in which m is the mass of the particle and the momentum operator is:
- where
Here is h/2π, where h is Planck's constant, and the Laplacian operator ∇2 is:
Although this is not the technical definition of the Hamiltonian in classical mechanics, it is the form it most commonly takes in quantum mechanics. Combining these together yields the familiar form used in the Schrödinger equation:
For hydrogen-like (one-electron) atoms, the Schrödinger equation can be written as:
where Z is the nuclear charge, e is the electron charge, and r is the position of the electron. The radial potential term on the right side of the equation is due to the Coulomb interaction, i.e., the electrostatic attraction between the nucleus and the electron, in which ε0 is the dielectric constant (permittivity of free space) and
is the 2-body reduced mass of the nucleus of mass mn and the electron of mass me. To a good approximation, µ ≈ me.

This is the equation that Erwin Schrödinger famously derived in 1926 to solve for the energies and shapes of the s, p, d, and f atomic orbitals in hydrogen-like atoms. It was a huge conceptual leap for both physics and chemistry because it not only explained the quantized energy levels of the hydrogen atom, but also provided the theoretical basis for the octet rule and the arrangement of elements in the periodic table.
The Schrödinger equation can be used to describe chemical systems that are more complicated than the hydrogen atom (e.g., multi-electron atoms, molecules, infinite crystals, and the dynamics of those systems) if we substitute the appropriate potential energy function V(r,t) into the Hamiltonian. The math becomes more complicated and the equation must be solved numerically in those cases, so for our purposes we will stick with the simplest case of time-invariant, one-electron, hydrogen-like atoms.

Without going into too much detail about the Schrödinger equation, we can point out some of its most important properties:
- The equation derives from the fact that the total energy (E) is the sum of the kinetic energy (KE) and the potential energy (PE). These three quantities are represented mathematically as operators in the equation.
- On the left side of the equation, the total energy operator (E) is a scalar that is multiplied by the wavefunction ψ. ψ is a function of the spatial coordinates (x,y,z) and is related to the probability that the electron is at that point in space.
- The first term on the right side of the equation represents the kinetic energy (KE). The kinetic energy operator is proportional to ∇2 (the Laplacian operator) which takes the second derivative (with respect to three spatial coordinates) of ψ. Thus, the Schrödinger equation is a differential equation.
- The second term on the right side of the equation represents the Coulomb potential (PE), i.e. the attractive energy between the positively charged nucleus and the negatively charged electron.
- The solutions to the Schrödinger equation are a set of energies E (which are scalar quantities) and wavefunctions (a.k.a. atomic orbitals) ψ, which are functions of the spatial coordinates. You will sometimes see the energies referred to as eigenvalues and the orbitals as eigenfunctions, because mathematically the Schrödinger equation is an eigenfunction-eigenvalue equation. Although ψ is a function of the coordinates, E is not. So an electron in a 2pz orbital has the same total energy E (= PE + KE) no matter where it is in space.
- These E values and their associated wavefunctions ψ are catalogued according to their quantum numbers n, l, and ml. That is, there are many solutions to the differential equation, and each solution (ψ(xyz) and E) has a unique set of quantum numbers. Some sets of orbitals are degenerate, meaning that they have the same energy (e.g., 2px, 2py, and 2pz).
- The solutions ψ(xyz) to the Schrödinger equation (e.g., the 1s, 2s, 2px, 2py, and 2pz orbitals) represent probability amplitudes for finding the electron at a particular point (x,y,z) in space. A probability amplitude can have either + or - sign. We typically represent the different signs by shading or by + and - signs on the two lobes of a 2p orbital.
- The square of the probability amplitude, ψ2, is always a positive number and represents the probability of finding the electron at a point x,y,z in space. Because the total probability of finding the electron somewhere is 1, the wavefunction must be normalized so that the integral of ψ2 over the spatial coordinates (from -∞ to +∞) is 1.
- The solutions to the Schrödinger equation are orthogonal, meaning that the product of any two (integrated over all space) is zero. For example the product of the 2s and 2px orbitals, integrated over the spatial coordinates from -∞ to +∞, is zero.
Orbital hybridization involves making linear combinations of the atomic orbitals that are solutions to the Schrödinger equation. Mathematically, this is justified by recognizing that the Schrödinger equation is a linear differential equation. As such, any sum of solutions to the Schrödinger equation is also a valid solution. However, we still impose the constraint that our hybrid orbitals must be orthogonal and normalized.
Rules for orbital hybridization:
- Add and subtract atomic orbitals to get hybrid orbitals.
- We get the same number of orbitals out as we put in.
- The energy of a hybrid orbital is the weighted average of the atomic orbitals that make it up.
- The coefficients are determined by the constraints that the hybrid orbitals must be orthogonal and normalized.
For sp hybridization, as in the BeF2 or CO2 molecule, we make two linear combinations of the 2s and 2pz orbitals (assigning z as the axis of the Be-F bond):
Here we have simply added and subtracted the 2s and 2pz orbitals; we leave it as an exercise for the interested student to show that both orbitals are normalized (i.e., ∫ψ12dτ = ∫ψ22dτ = 1) and orthogonal (i.e., ∫ψ1ψ2dτ = 0).
What this means physically is explained in the figure below. By combining the 2s and 2pz orbitals we have created two new orbitals with large lobes (high electron probability) pointing along the z-axis. These two orbitals are degenerate and have an energy that is halfway between the energy of the 2s and 2pz orbitals.

For an isolated Be atom, which has two valence electrons, the lowest energy state would have two electrons spin-paired in the 2s orbital. However, these electrons would not be available for bonding. By promoting these electrons to the degenerate 2spz hybrid orbitals, they become unpaired and are prepared for bonding to the F atoms in BeF2. This will occur if the bonding energy (in the promoted state) exceeds the promotion energy. The overall bonding energy, i.e., the energy released by combining a Be atom in its ground state with two F atoms, is the difference between the bonding and promotion energies.
We can similarly construct sp2 hybrids (e.g., for the BF3 molecule or the NO3- anion) from one 2s and two 2p atomic orbitals. Taking the plane of the molecule as the xy plane, we obtain three hybrid orbitals at 120° to each other. The three hybrids are:

These orbitals are again degenerate and their energy is the weighted average of the energies of the 2s, 2px, and 2py atomic orbitals.
Finally, to make a sp3 hybrid, as in CH4, H2O, etc., we combine all four atomic orbitals to make four degenerate hybrids:


The lobes of the sp3 hybrid orbitals point towards the vertices of a tetrahedron (or alternate corners of a cube), consistent with the tetrahedral bond angle in CH4 and the nearly tetrahedral angles in NH3 and H2O. Similarly, we can show that we can construct the trigonal bipyramidal electronic shape by making sp and sp2 hybrids, and the octahedral geometry from three sets of sp hybrids. The picture that emerges from this is that the atomic orbitals can hybridize as required by the shape that best minimizes electron pair repulsions.

Interestingly however, the bond angles in PH3, H2S and H2Se are close to 90°, suggesting that P, S, and Se primarily use their p-orbitals in bonding to H in these molecules. This is consistent with the fact that the energy difference between s and p orbitals stays roughly constant going down the periodic table, but the bond energy decreases as the valence electrons get farther away from the nucleus. In compounds of elements in the 3rd, 4th, and 5th rows of the periodic table, there thus is a decreasing tendency to use s-p orbital hybrids in bonding. For these heavier elements, the bonding energy is not enough to offset the energy needed to promote the s electrons to s-p hybrid orbitals.
1.3 Bond polarity and bond strength
[edit | edit source]
Linus Pauling introduced the concept of electronegativity 1932 in order to explain the extra stability of molecules with polar bonds. [12] The electronegativity of an atom, represented by the Greek letter χ, can be defined as the tendency of an atom to draw electrons to itself in a chemical bond. On the Pauling scale, the electronegativity difference between two atoms A and B was defined in terms of the dissociation energies Ed of the A-A, B-B, and A-B bonds:
where the energies are expressed in electron volts.
This definition, while directly relevant to the strength of chemical bonds, requires thermochemical input data from many compounds, some of which were not available at the time. Mulliken[13][14] and later Pearson[15] developed a scale of electronegativities based on the average of the electron affinity and ionization energy of the free A and B atoms, which they correlated with thermochemical data and the Pauling scale.
On the Pauling scale, the least electronegative elements are the alkali metals (χ = 0.7-1.0) and the most electronegative are oxygen (3.5) and fluorine (4.0) at the upper right of the periodic table. Carbon and hydrogen have intermediate electronegativities (2.6 and 2.2 on the Pauling scale, respectively). The general trend (see table below) is that electronegativities increase going up and to the right in the periodic table. There are some interesting exceptions to this behavior, most notably two islands of high electronegativity at the bottom of the transition series, peaking at tungsten (χ = 2.4) and gold (χ = 2.5). The first of these can be explained by the very high metal-metal bond energy of elements such as Mo and W, which can use all six of their valence electrons in bonding, as we will discuss in Chapter 6. The second however occurs with more weakly bonded noble metals such as Pt and Au, and is responsible for their low position in the activity series,[16] as well as their extraordinary properties as catalysts.

Table of Pauling electronegativities
The polarity of bonds is determined by electronegativity differences. As a guideline we define bonds as:
- ionic if Δχ > 2.0
- polar if 2.0 > Δχ > 0.5
- nonpolar if 0.5 > Δχ
The polarity of bonds helps us understand non-covalent forces between molecules, such as hydrogen bonding and dipole-dipole interactions. It also helps us interpret the reactivity of molecules. For example, the Si-H bond (χSi = 1.8, χH = 2.1) is more hydride-like than the C-H bond (χC = 2.5, χH = 2.1). Therefore silanes react with acids to make H2, whereas phosphines (χP = 2.1) and hydrocarbons do not. Similarly, electrophilic substitution reactions occur more readily on Si-H and P-H compounds than they do on C-H compounds.
There is also a correlation between the strength of a chemical bond and the bond length, longer bonds being weaker because of weaker orbital overlap. Pauling introduced an empirical formula relating bond length to bond strength. For a given pair of atoms (for example, two carbon atoms):
- D(n) = D(1) - 0.6 log10(n)
where D(n) represents the bond length in Å and n is the bond order. D(1) in this case would be the length of a C-C single bond, which we can obtain from the average bond length in alkanes (1.54 Å). Using this formula we can predict that the bond lengths in ethylene (C=C double bond) and acetylene (C≡C triple bond) should be 1.36 and 1.25 Å, respectively, which are close to the experimental values of 1.33 and 1.20 Å. In a related form the Pauling formula can be used to calculate bond lengths when the single bond length D(1) is not available:
- D(n) = D(m) - 0.6 log10(n/m)
Here n and m represent two different bond orders between the same kinds of atoms. This tells, for example, that the difference in length between a triple and double bond, D(2)-D(3), should be - 0.6 log10(2/3) = 0.11 Å.

Some bond lengths and bond energies are anomalous. For example, the F-F bond length in F2 is 1.43 Å, which is 0.15 Å longer than twice the covalent radius of the F atom (0.64 Å). The F-F bond is also quite weak (bond dissociation energy = 155 kJ/mol) relative to the Cl-Cl bond (242 kJ/mol). By putting the extra bond length into the Pauling formula, we calculate that the bond order in the F2 molecule is only 0.6, i.e., substantially weaker than a F-F single bond. The physical reason for this is that the F-F bond is "stretched" by repulsion of the lone pairs on the F atoms. This crowding is caused by the fact that the [He] 1s2 core orbital, as well as the valence orbitals of the fluorine atoms, are contracted by the high nuclear charge. The Cl atom in Cl2 has a larger [Ne] (1s22s22p6) core, in contrast, so Cl-Cl has a "normal" single bond length (1.98 Å) that is twice the covalent radius of the Cl atom (0.99 Å). A similar lone pair repulsion effect explains the anomalously long and weak N-N and O-O single bonds in hydrazine (H2N-NH2) and hydrogen peroxide (HO-OH), which are both highly reactive molecules.
The important roles of electronegativity differences and lone pair repulsion are evident when comparing trends in bond strengths. The table below shows the average single-bond enthalpies of p-block elements with H and F. H makes stronger bonds with 2nd row elements (C, N, O, F) than with third row elements (Si, P, S, Cl) because the 2p valence electrons are closer to the nucleus and thus make stronger bonds than electrons in 3p orbitals. The bonds to H also follow the expected trend of increasing bond strength with increasing electronegativity difference. Bonds between second row elements (C, N, O, F) and F are however anomalously weak because of lone pair repulsion. For this reason, the Si-F bond is substantially stronger than the C-F bond, whereas the C-H bond is much stronger than the Si-H bond. The strong Si-F bond is the reason that HF etches glass (to produce the SiF62- anion), and the strong C-H bond is an important factor in the stability of hydrocarbons and other organic molecules.
Average E-H and E-F bond enthalpies (kJ/mol)
| C-H 413 | N-H 391 | O-H 483 | H-F 567 |
| Si-H 323 | P-H 322 | S-H 339 | H-Cl 431 |
|
|
|||
| C-F 485 | N-F 272 | O-F 190 | F-F 155 |
| Si-F 565 | P-F 490 | S-F 327 | Cl-F 253 |

The anomalously weak bond in F2 is responsible for the high electronegativity of fluorine, as well as the legendary reactivity of elemental fluorine gas, which reacts explosively with hydrogen and powdered metals. Because of the instability of elemental fluorine and the polar nature of its bonds with more electropositive elements, fluorine compounds tend to be very stable. For example, the noble gases Xe and Kr react with fluorine to make covalent compounds, whereas other halogens do not react. Fluorocarbon compounds contain strong C-F bonds and have high thermal and chemical stability. Perfluorocarbons such as Teflon (poly(tetrafluoroethylene), -(CF2CF2)n-, PTFE) are also highly hydrophobic. The extraordinary hydrophobicity of perfluorocarbons arises from the fact that -CF2- and -CF3 groups are "fatter" than -CH2- and -CH3 groups; dissolving them in water is therefore more disruptive to the hydrogen bonding network than is dissolving a hydrocarbon. [21]
1.4 Discussion questions
[edit | edit source]Group essay project:
Join a group of classmates from your inorganic chemistry course. Each group should have 3 or 4 students. Arrange a time to meet for an hour or so. Prior to the meeting, read part I (pp. 1367-1391) as well as the summary at the end of Linus Pauling's article (J. Am. Chem. Soc. 1931, 53, 1367-1400) on the nature of the chemical bond.
This paper was published only a few years after Schrödinger developed the quantum mechanical theory of atomic orbitals and is considered one of the most important papers in the history of modern chemistry. At the meeting, discuss the following questions: (1) What was understood about chemical bonding in molecules before Pauling published this work? (2) What new concepts did the paper introduce that we still use today? (3) Why were these ideas important? and (4) What, if anything, did Pauling get wrong, and why?
Together with your classmates, write a 1-2 page essay addressing these questions. Please include the names of all students in your group on the first page; all of you will receive the same grade on this assignment. Anonymous excerpts from a few of these essays will be shared with the class.
In-class discussion questions from this chapter:
- What are inequivalent resonance structures? Illustrate with some new examples not covered above.
- Explain no-bond resonance and hypervalency, using some new examples.
- What are the limitations of valence bond theory for molecules that contain an odd number of electrons? Illustrate with one or two examples.
1.5 Problems
[edit | edit source]1. Draw composite octet structures (including formal charges, bond order, and molecular shape) for the following: (a) BrO3-, (b) SF6, (c) KrF2, (d) HClO4 (= HOClO3), (e) NO2-, and (f) ClO2.
2. Draw composite octet structures (including formal charges, bond order, and molecular shape) for the following: (a) Al2Cl6, (b) SnCl3-, (c) BrF4-,(d) HOClO, (e) SO3, and (f) NO2+.
3. Show using resonance why the CO bond distance in formamide (HCONH2) is longer than the CO bond distance in acetone.
4. Give the formulas for five stable molecules and/or ions that are isoelectronic with ammonia.
5. Name three well known molecules or ions that are isoelectronic with (a) NO2+, (b) BF4-, (c) CH4, and (d) HCN.
6. Name three well known molecules or ions that are isoelectronic with (a) CN-, (b) H2O, (c) BF3, and (d) CO2.
7. The C-C bond distance is 1.20 Å in acetylene. Using the Pauling bond length – bond strength formula, D(n) = D(1) - 0.6 log(n), estimate the C-C bond distance in ketene (H2CCO).
8. In hydroxylamine, H2NOH, the N-O bond distance is 1.46 Å. Using the Pauling bond length - bond strength formula, estimate the N-O bond distances in NO2 and NO3-.
9. Nitrogen can exist in the +5 oxidation state in compounds that contain ions such a NF4+ and NO3-. However the neutral binary compound NF5 is unknown. Can you draw octet structures for each of these compounds? Why would NF5 be unstable?
10. Consider the compounds NH3 and PH3. The H-N-H bond angle in ammonia is 108o (close to the tetrahedral angle, 109.5o), but the analogous angle in PH3 is 93o. Why is the angle in PH3 closer to 90o than it is to the tetrahedral angle?
11. Two hypothetical structures for the N2F3+ ion are [N-NF3]+ and [F-N-NF2]+. Which one is more stable? Explain. (Note: lines in the formulas can represent either single or multiple bonds)
12. Krypton difluoride, KrF2, decomposes at dry ice temperature to Kr and F2. However, several salts of the [KrF]+ ion are relatively stable. Draw valence bond pictures for KrF2 and [KrF]+, showing lone pairs, possible resonance structures, formal charges, bond orders, and bond angles. Why is [KrF]+ more stable than KrF2?
13. Consider the anion SF3O2- (with S the central atom). How many isomers are possible? Which is the most stable?
14. The Br-F bond distance in the interhalogen compound BrF is 1.76 Å. Use this information to estimate the average bond lengths in BrF3 and BrF5.
15. The B-H bond distances are about the same in BH3 and BH4-. however, the B-F bond distance in BF3 is shorter than that in the BF4- ion. Explain.
16. The N-N bond dissociation energy in hydrazine (H2N-NH2) is 159 kJ/mol. The dissociation energy of the N-N triple bond in N2 is 941 kJ/mol, i.e., much greater than three times the N-N single bond dissociation energy in hydrazine. Explain why the N-N bond in hydrazine is so weak, and why this effect is not seen in N2.
17. Show that a set of four sp3 hybrid orbitals satisfies the following criteria: (a) any two orbitals in the sp3 set are orthogonal, and (b) the orbitals are properly normalized.
18. Quantum mechanically, the momentum (p) of a particle traveling in a specific direction (e.g., the x direction) can be obtained by operating on its wavefunction with the momentum operator:
- , where
Knowing the correct form of this operator was the key to Schrödinger's formulation of the Hamiltonian operator, , which operates on a wavefunction to give the total energy. The momentum operator must also be consistent with the de Broglie relation, p = h/λ, which relates the momentum to the particle wavelength.
By analogy to electromagnetic waves, Schrödinger knew that a wavelike particle (such as an electron) traveling in free space in the x-direction could be described by the wavefunction:
where the wavenumber k is inversely related to the particle's de Broglie wavelength λ by k = 2π/λ. Here A is a normalization constant, ω is the frequency of the wave, and represents its phase.
Show using the momentum operator that the value of the momentum p we obtain for a free particle from is consistent with the de Broglie relation, p = h/λ.
(Hint: k, ω, and are independent of x)
19. N3S4+ is a cyclic cation that contains no N-N bonds. Draw the structure of the seven-membered ring and use the electron counting method to determine the number of single bonds, double bonds, and lone pairs. Draw out the possible resonance structures for this ion showing formal charges and indicate which one is the most stable.
20. F has a higher electronegativity than Cl, and F2 is a much stronger oxidizing agent than Cl2, despite the fact that the electron affinity of fluorine (-328 kJ/mol) is weaker than that of chlorine (-349 kJ/mol). Explain this apparent contradiction.
21. The single bonds in methane (CH4), ammonia (NH3) and water (H2O) are stronger than those in SiH4, PH3, and H2S, respectively. The analogous fluorine containing compounds follow the opposite trend: the single bonds in CF4, NF3, and OF2 are weaker than those in SiF4, PF3, and SF2. Can you explain these two opposite trends?
1.6 References
[edit | edit source]- ↑ G. N. Lewis, "The atom and the molecule," J. Am. Chem. Soc. 1916, 38, 762-785
- ↑ W. Saenger, "The structure of the blue starch-iodine complex," Naturwissenschaften 71, 31-36 (1984).
- ↑ R. D. Hancock and B. J. Tarbet, "The other double helix - the fascinating chemistry of starch," J. Chem. Ed. 77, 988-992 (2000).
- ↑ R. J. Gillespie and B. Silvi, "The octet rule and hypervalence: two misunderstood concepts," Coord. Chem. Rev. 233-234, 53-62 (2002).
- ↑ I. Chung, B. Lee, J. He, R. P. H. Chang and M. G. Kanatzidis, All-solid-state dye-sensitized solar cells with high efficiency, Nature 485, 486-489 (2012). doi:10.1038/nature11067
- ↑ S.D. Stranks, G. E. Eperon, G. Grancini, C. Menelaou, M. J. P. Alcocer, T. Leijtens, L. M. Herz, A. Petrozza, and H. J. Snaith, Electron-Hole Diffusion Lengths Exceeding 1 Micrometer in an Organometal Trihalide Perovskite Absorber, Science 342, 341-344 (2013). DOI: 10.1126/science.1243982
- ↑ G. Xing, N. Mathews, S. Sun, S. S. Lim, Y. M. Lam, M. Grätzel, S. Mhaisalkar, and T. C. Sum, Long-Range Balanced Electron- and Hole-Transport Lengths in Organic-Inorganic CH3NH3PbI3, Science 342, 344-347 (2013). DOI: 10.1126/science.1243167
- ↑ J.-P. Correa-Baena, A. Abate, M. Saliba, W. Tress, T. J. Jacobsson, M. Grätzel, and A. Hagfeldt, The rapid evolution of highly efficient perovskite solar cells, Energy Environ. Sci., 10, 710-727 (2017). DOI: 10.1039/C6EE03397K
- ↑ N. V. Sidgwick and H. M. Powell, Proc. Roy. Soc. A176, 153 (1940),
- ↑ R. J. Gillespie and R. S. Nyholm, Quart. Rev. Chem. Soc., 11, 339 (1957).
- ↑ R. J. Gillespie, "Fifty years of the VSEPR model," Coord. Chem. Rev. 252, 1315-1327 (2008). DOI: 10.1016/j.ccr.2007.07.007
- ↑ Pauling, L. (1932). "The Nature of the Chemical Bond. IV. The Energy of Single Bonds and the Relative Electronegativity of Atoms". J. Am. Chem. Soc. 54 (9): 3570–3582. doi:10.1021/ja01348a011.
- ↑ Mulliken, R. S. (1934). "A New Electroaffinity Scale; Together with Data on Valence States and on Valence Ionization Potentials and Electron Affinities". J. Chem. Phys. 2 (11): 782–793. Bibcode:1934JChPh...2..782M. doi:10.1063/1.1749394.
- ↑ Mulliken, R. S. (1935). "Electronic Structures of Molecules XI. Electroaffinity, Molecular Orbitals and Dipole Moments". J. Chem. Phys. 3 (9): 573–585. Bibcode:1935JChPh...3..573M. doi:10.1063/1.1749731.
- ↑ Pearson, R. G. (1985). "Absolute electronegativity and absolute hardness of Lewis acids and bases". J. Am. Chem. Soc. 107 (24): 6801. doi:10.1021/ja00310a009.
- ↑ B. Hammer and J. K. Norskov, "Why gold is the noblest of all the metals," Nature 376, 238 - 240 (2002. doi:10.1038/376238a0
- ↑ Schomaker, Verner; Stevenson, D. P. (1941). "Some Revisions of the Covalent Radii and the Additivity Rule for the Lengths of Partially Ionic Single Covalent Bonds *". Journal of the American Chemical Society. 63: 37–40. doi:10.1021/ja01846a007.
- ↑ Pauling, L. The Nature of the Chemical Bond, 3rd ed.; Cornell University Press: Ithaca, NY, 1960; p. 224.
- ↑ Robinson, Edward A.; Johnson, Samuel A.; Tang, Ting-Hua; Gillespie, Ronald J. (1997). "Reinterpretation of the Lengths of Bonds to Fluorine in Terms of an Almost Ionic Model". Inorganic Chemistry. 36 (14): 3022–3030. doi:10.1021/ic961315b. PMID 11669953.
- ↑ Pyykkö, Pekka; Atsumi, Michiko (2009). "Molecular Double-Bond Covalent Radii for Elements Li–E112". Chemistry: A European Journal. 15 (46): 12770–12779. doi:10.1002/chem.200901472.
- ↑ V. H. Dalvi and P. J. Rossky, Molecular origins of fluorocarbon hydrophobicity, Proc. Natl. Acad. Sci. USA 107,13603–13607 (2010). DOI: 10.1073/pnas.0915169107.

































![{\displaystyle \chi _{\rm {A}}-\chi _{\rm {B}}={\sqrt {E_{\rm {d}}({\rm {AB}})-[E_{\rm {d}}({\rm {AA}})+E_{\rm {d}}({\rm {BB}})]/2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93475ab1444be44f5df567732672dcef9630e8b3)






