Introduction to Inorganic Chemistry/Ionic and Covalent Solids - Energetics
Chapter 9: Ionic and Covalent Solids - Energetics
[edit | edit source]
In Chapter 8, we learned all about crystal structures of ionic compounds. A good question to ask is, what makes a compound choose a particular structure? In addressing this question, we will learn about the forces that hold crystals together and the relative energies of different structures. This will in turn help us understand in a more quantitative way some of the heuristic concepts we have learned about in earlier chapters, such as hard-soft acid-base theory.
Learning goals for Chapter 9:
- Understand the geometric basis of radius ratio rules.
- Understand the chemical basis of structure maps and why they are better predictors of crystal structures than radius ratios.
- Use the Born-Mayer and Kapustinskii equations to calculate lattice energies of known and hypothetical compounds.
- Construct Born-Haber cycles using lattice energies and calculate unknown quantities in the cycles.
- Predict the stabilities of low and high oxidation states using lattice energies.
- Understand the quantum mechanical origin of the extra "resonance" stability of metals.
- Predict trends in the solubility and thermal stability of inorganic compounds using lattice energies.
9.1 Ionic radii and radius ratios
[edit | edit source]Atoms in crystals are held together by electrostatic forces, van der Waals interactions, and covalent bonding. It follows that arrangements of atoms that can maximize the strength of these attractive interactions should be most favorable and lead to the most commonly observed crystal structures.

Radius ratio rules. Early crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was (and still is!) important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii. Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.

The basic idea of radius ratio rules is illustrated at the right. We consider that the anion is the packing atom in the crystal and the smaller cation fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbor anions, as shown at the right for a small cation in contact with larger anions, then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.
| Coordination number | Geometry | ρ = rcation/ranion |
|---|---|---|
There are unfortunately several challenges with using this idea to predict crystal structures:
- We don't know the radii of individual ions
- Atoms in crystals are not really ions - there is a varying degree of covalency depending electronegativity differences
- Bond distances (and therefore ionic radii) depend on bond strength and coordination number (remember Pauling's rule D(n) = D(1) - 0.6 log n)
- Ionic radii depend on oxidation state (higher charge => smaller cation size, larger anion size)
We can build up a table of ionic radii by assuming that the bond length is the sum of the radii (r+ + r-) if the ions are in contact in the crystal. Consider for example the compounds MgX and MnX, where X = O, S, Se. All of these compounds crystallize in the NaCl structure:
bond distance (rMX)
- MgO 2.10 MgS 2.60 MgSe 2.73 Å
- MnO 2.24 MnS 2.59 MnSe 2.73 Å

For the two larger anions (S2- and Se2-), the unit cell dimensions are the same for both cations. This suggests that the anions are in contact in these structures. From geometric considerations, the anion radius in this case is given by:
and thus the radii of the S2- and Se2- ions are 1.84 and 1.93 Å, respectively. Once the sizes of these anions are fixed, we can obtain a self-consistent set of cation and anion radii from the lattice constants of many MX compounds.
How well does this model work? Let's consider the structures of tetravalent metal oxides (MO2), using Pauling radii and the predictions of the radius ratio model:
| Oxide MO2 | Radius ratio | Predicted coord. no. | Observed coord no. (structure) |
|---|---|---|---|
| 2 (linear molecule) | |||
| 4 (various tetrahedral structures) | |||
| 4 (silica-like structures) | |||
| 6 (rutile) | |||
| 6 (rutile) | |||
| 7 (baddleyite) | |||
| 8 (fluorite) | |||
| 8 (fluorite) |
Note that cations have different radii depending on their coordination numbers, and thus different radius ratios are calculated for Ge4+ with coordination numbers 4 and 6, and for Zr4+ with coordination numbers 6 and 8.
For this series of oxides, the model appears to work quite well. The correct coordination number is predicted in all cases, and borderline cases such as GeO2 and ZrO2 are found in structures with different coordination numbers. The model also correctly predicts the structures of BeF2 (SiO2 type), MgF2 (rutile), and CaF2 (fluorite).
What about the alkali halides NaCl, KBr, LiI, CsF, etc.? All of them have the NaCl structure except for CsCl, CsBr, and CsI, which have the CsCl (8-8) structure. In this case the radius ratio model fails rather badly. The Li+ salts LiBr and LiI are predicted to have tetrahedral structures, and KF is predicted to have an 8-8 structure like CsCl. We can try adjusting the radii (e.g., making the cations larger and anions smaller), but the best we can do with the alkali halides is predict about half of their structures correctly. Since the alkali halides are clearly ionic compounds, this failure suggests that there is something very wrong with the radius ratio model, and its success with MO2 compounds was coincidental.
In addition to the radius ratio rule, Linus Pauling developed other useful rules that are helpful in rationalizing and also predicting the structures of inorganic compounds. Pauling's rules[1] state that:
- Stable structures are locally electroneutral. For example, in the structure of the double perovskite Sr2FeMoO6, MO6 (M = Fe2+, Mo6+) octahedra share all their vertices, and Sr2+ ions fill the cubooctahedral cavities that are flanked by eight MO6 octahedra.[2] Each O2- ion is coordinated to one Fe2+ and one Mo6+ ion in order to achieve local electroneutrality, and thus the FeO6 and MoO6 octahedra alternate in the structure.
- Cation-cation repulsion should be minimized. Anion polyhedra can share vertices (as in the perovskite structure) without any energetic penalty. Shared polyhedral edges, and especially shared faces, cause cation-cation repulsion and should be avoided. For example, in rutile, the most stable polymorph of TiO2, the TiO6 octahedra share vertices and two opposite edges, forming ribbons in the structure. In anatase TiO2, each octahedron shares four edges so the anatase polymorph is less thermodynamically stable.
- Highly charged cations in anion polyhedra tend not to share edges or even vertices, especially when the coordination number is low. For example, in orthosilicates such as olivine (M2SiO4), there are isolated SiO44- tetrahedra.
As we will soon see, all of Pauling's rules are justified on the basis of lattice energy considerations. In ionic compounds, the arrangement of atoms that maximizes anion-cation interactions while minimizing cation-cation and anion-anion contacts is energetically the best.
9.2 Structure maps
[edit | edit source]
Structure maps, which plot structures against properties such electronegativity, are more consistent than radius ratio rules in correctly predicting coordination numbers and crystal structures. One of the early examples of this approach was published by Mooser and Pearson in 1959.[3]
A Mooser-Pearson diagram maps crystal structures according to the average principal quantum numbers of the atoms and their electronegativity difference. The basic ideas behind such a plot are:
- The greater the electronegativity difference, the more ionic is the compound. Higher ionicity results in higher coordination numbers because anions like to surround cations (and vice versa).
- Higher principal quantum numbers result in less s-p hybridization, less directional bonding, and therefore higher coordination number. We saw this trend before with the structures of elements in group IV: descending the group the coordination number increases progressively from 3-4 (carbon) to 12 (Pb).
The lines in the Mooser-Pearson diagram separate MX compounds with CsCl, NaCl, and tetrahedral (wurtzite and zincblende) structures. Note that wurtzite has higher ionicity than zincblende in the plot, consistent with our discussion of the "boat" and "chair" ring structures in Chapter 8. Diamorphic compounds tend to fall on the boundaries. On the whole, the Mooser-Pearson diagram makes far fewer errors in predicting structures than the radius ratio rule. There are similar diagrams for MX2 structures, in which the order of ionicity is CaF2 (8:4 coordination) > rutile (6:3) > silica structures (4:2).
9.3 Energetics of crystalline solids: the ionic model
[edit | edit source]
Many ionic compounds have simple structures. Because the forces holding the atoms together are primarily electrostatic, we can calculate the cohesive energy of the crystal lattice with good accuracy. Interesting questions to ask about these lattice energy calculations are:
- How accurate are lattice energy calculations?
- What do they teach us about the chemical bonds in ionic crystals?
- Can we use lattice energies to predict properties such as solubility, stability, and reactivity?
- Can we use lattice energies to predict the crystal structures of ionic compounds?
Let's start by looking at the forces that hold ionic lattices together. There are mainly two kinds of force that determine the energy of an ionic bond.
1) Electrostatic Force of attraction and repulsion (Coulomb's Law): Two ions with charges z+ and z-, separated by a distance r, experience a force F:
- where
- e = 1.6022×10−19 C
- 4 π ε0 = 1.112×10−10 C²/(J m)
This force is attractive for ions of opposite charge.
The electrostatic potential energy, Eelec, is then given by
The sign of Eelec is negative for the attractive interaction between a cation and an anion. That is, the closer oppositely charged ions approach each other, the lower the potential energy.

2) Closed-shell repulsion. When electrons in the closed shells of one ion overlap with those of another ion, there is a repulsive force comes from the Pauli exclusion principle. A third electron cannot enter an orbital that already contains two electrons. This force is short range, and is typically modeled as falling off exponentially or with a high power of the distance r between atoms. For example, in the Born approximation, B is a constant and ρ is a number with units of length, which is usually empirically determined from compressibility data. A typical value of ρ is 0.345 Å.
The energy of the ionic bond between two atoms is then calculated as the combination of net electrostatic and the closed-shell repulsion energies, as shown in the figure at the right. Note that for the moment we are ignoring the attractive van der Waals energy between ions, which we will explain below. For a pair of ions, the equilibrium distance between ions is determined by the minimum in the total energy curve. At this distance, the net force on each ion is zero.

Electrostatic energy of a crystal lattice. We can use these equations to calculate the lattice energy of a crystal by summing up the interactions between all pairs of ions. Because the closed-shell repulsion force is short range, this term is typically calculated only for interactions between neighboring ions. However, the Coulomb force is long range, and must be calculated over the entire crystal. This problem was first solved in 1918 by Erwin Madelung, a German physicist.[4]
Consider an ion in the NaCl structure labeled "O" in the diagram at the right. We can see that the nearest neighbor interactions (+ -) with ions labeled "1" are attractive, the next nearest neighbor interactions (- - and + +) are repulsive, and so on. In the NaCl structure, counting from the ion in the center of the unit cell, there are 6 nearest neighbors (on the faces of the cube), 12 next nearest neighbors (on the edges of the cube), 8 in the next shell (at the vertices of the cube), and so on. Their distances from ion "0" increase progressively: ro, √2 ro, √3 ro, and so on, where ro is the nearest neighbor distance.
We can now write the electrostatic energy at ion "O" as:
Factoring out constants and the nearest-neighbor bond distance ro we obtain:
Where the sum in parentheses, which is unitless, slowly converges to a value of A = 1.74756. Generalizing this formula for any three-dimensional ionic crystal we get a function:
where N is Avogadro's number (because we are calculating energy per mole of ions) and A is called the Madelung constant. The Madelung constant depends only on the geometrical arrangement of the ions and so it varies between different types of crystal structures, but within a given structure type it does not change. Thus MgO and NaCl have the same Madelung constant because they both have the NaCl structure.
The table below lists Madelung constants for some common structures. The reduced Madelung constant is obtained by normalizing the values to the number of ions in the formula unit. It can be seen from the table that the reduced Madelung constants are quite similar for different structures. This makes it hard to determine on the basis of electrostatic energy calculations which structure will be most stable for a given compound. It is interesting to note that the trend in reduced Madelung constants roughly follows the trend in ionicity (cf. the Mooser-Pearson diagram in Section 9.2). For example, wurtzite has a slightly higher Madelung constant than zincblende, consistent with our earlier conclusion that the wurtzite structure is favored by more polar compounds.
| Structure | Madelung Constant, A | Reduced Madelung Constant, 2A/n |
|---|---|---|

Total lattice energy of a crystal. Having in hand a formula for the electrostatic energy, we can now add in the closed-shell repulsion term to obtain an equation that gives us the total lattice energy.
At the equilibrium bond distance, the forces on all the ions are zero, and we can use this fact to eliminate the constant B:
From this we obtain the Born-Mayer equation:
Expressed this way, EL is a negative number (because z+ and z- have opposite signs). It represents the energy change for forming one mole of solid salt from one mole of the gaseous ions, separated initially at an infinite distance.
9.4 Born-Haber cycles for NaCl and silver halides
[edit | edit source]Now that we have an equation for the lattice energy of an ionic crystal, we can ask the question of how accurate it is. Remember, we made several approximations in arriving at this formula. We assumed that the lattice was completely ionic, we ignored the van der Waals attractive energy of the ions, and we assumed that there was no covalent contribution to the bonding.
Let's consider the lattice energy of table salt (NaCl)
Na+(g) + Cl-(g) --> NaCl(s)
To calculate the lattice energy, we lump together the physical constants:
where ro is expressed in Å. Now we can calculate the lattice energy for NaCl using ro = 2.814 Å, as:
- kJ/mol
We can alternatively construct a Born-Haber cycle for the formation of NaCl from the elements and calculate the lattice energy as the "missing" term in the cycle.

S= Sublimation energy of Na(s)
IP= Ionization potential of Na(g)
D= Bond dissociation energy of Cl2(g)
EA= Electron affinity of Cl(g)
EL=Lattice energy of NaCl
R= Gas constant
T= Absolute temperature
From Hess' Law: ΔHf = S + 1/2D + IP + EA + EL - 2RT = -396 kJ/mol
Here we have to subtract 2RT to convert our cycle of energies to a cycle of enthalpies, because we are compressing two moles of gas in making NaCl(s) and PΔV = ΔnRT, where Δn = -2.
Experimentally ΔHf for NaCl is -411 kJ/mol
Because all the other numbers in the cycle are known accurately, the error in our calculation is only about 15 kJ (about 2% of EL). The result is promising because we neglected the van der Waals term.
But....how did we get away with neglecting the van der Waals term?
This is because we used energy minimization to obtain the repulsion energy in the Born-Mayer equation. If we underestimate the attractive energy of the crystal lattice, the energy minimization criterion ensures that the repulsion energy is underestimated as well. The two errors partially compensate, so the overall error in the calculation is small.
We can do better by explicitly including the short-range van der Waals attractive energy between ions. The table below shows results of more detailed lattice energy calculations for ionic fluorides in which the van der Waals term is explicitly included. The errors in this case are only about 1% of EL.
| Compound | Calculated Lattice Energy (kJ/mol) | Experimental EL from Born-Haber Cycle |
|---|---|---|
Silver Halides

It is interesting to repeat this exercise for the silver halides, which have either the NaCl structure (AgF, AgCl, AgBr) or zincblende structure (AgI).
| Silver Halide | Calculated | Cycle | Difference (kJ/mol) |
|---|---|---|---|
Looking at the table, we see that the error is small for AgF and becomes progressively larger for the heavier silver halides. However we are still obtaining answers within about 12% error even for AgI. Should we interpret the good agreement with values calculated from the ionic model to mean that these compounds are ionic? Clearly, this description is inappropriate for AgI, where the electronegativity difference Δχ is only 0.6 (compare this value to 0.4 for a C-H bond, which we typically view as non-polar).
Again, we can interpret the fortuitous agreement between the calculated and experimentally obtained energies in terms of compensating errors. Our lattice energy calculation overestimates the ionic contribution in the case of the heavier silver halides, but underestimates the covalent contribution. Of these compounds, only AgF is soluble in water and should be thought of as an ionic compound. The others are progressively more insoluble in water (Ksp is 10-10, 10-13, and 10-16 for AgCl, AgBr, and AgI), reflecting increasing covalency as Δχ decreases.
The moral of the story is that simple lattice energy calculations based on the ionic model work well, but they do not necessarily imply that the compounds are ionic!
9.5 Kapustinskii equation
[edit | edit source]From the discussion above, it is clear that the lattice energy, EL, of an ionic crystal can be calculated with reasonable accuracy if the structure is known. But how can we calculate EL for a new or hypothetical compound of unknown structure? Recall that the reduced Madelung constant is about the same for different crystal structures. Russian chemist A. F. Kapustinskii recognized this fact and devised a formula that allows one to calculate EL for any compound if we know the univalent radii of the constituent ions.[5]
The Madelung constant, A, is proportional to the number of ions (n) in formula unit, so dividing by the n gives similar values as shown in the table below:
A/n ~ invariant
| Structure | A/n |
|---|---|
| NaCl | 0.874 |
| CsCl | 0.882 |
| Rutile | 0.803 |
| Fluorite | 0.800 |
Kapustinskii noticed that the difference in ionic radii between M+ and M2+ (the monovalent vs. divalent radius) largely compensates for the differences in A/n between monovalent (NaCl, CsCl) and divalent (rutile, CaF2) structures. He thus arrived at a lattice energy formula using an average Madelung constant, corrected to monovalent radii. In the Kapustinskii formula, the lattice energy (kJ/mol) is given by:
Here the sum of the monovalent radii is used in place of ro, the bond distance in the Born-Mayer equation. The beauty of this formula is that it requires no knowledge of the structure of the compound. Therefore it can be used, in combination with Born-Haber cycles, to predict the stability of unknown compounds. As we show below, this is a broadly useful tool in guiding syntheses and predicting the reactivity of inorganic solids.
9.6 Discovery of noble gas compounds
[edit | edit source]
In 1962 at the University of British Columbia, Neil Bartlett was working with the powerful oxidizer PtF6 and, because of an accidental leak in his vacuum line, noticed the compound’s reaction with O2 to generate a solid with formula "PtF6O2." The formula suggested Pt in the +10 oxidation state, which was clearly unreasonable because PtF6 was known to be a more powerful oxidizer than either molecular fluorine (F2) or molecular oxygen (O2). Bartlett noticed that the X-ray powder diffraction pattern of the compound was similar to that of Cs+AsF6-, a salt with the CsCl structure in which octahedral AsF6- ions occupy the chloride ion sites. This led Bartlett to propose a formulation of O2+PtF6- for his new compound.[6] Magnetic susceptibility data subsequently confirmed the presence of the paramagnetic O2+ cation, which (see Chapter 2) has a bond order of 2.5. This formulation implies that PtF6 was a strong enough oxidizing agent to oxidize molecular oxygen.
But just how strong an oxidizer is PtF6? Its electron affinity could be estimated by using a Born-Haber cycle, filling in the lattice energy of O2+PtF6- by means of Kapustinskii's formula:
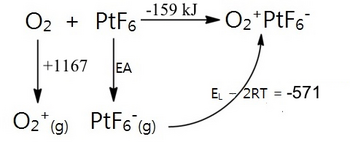
The electron affinity (EA) for PtF6 can be calculated as EA = -159 - 1167 + 571 = -751 kJ/mol. To put it in perspective, this is 417 kJ/mol more exothermic than the electron affinity of atomic fluorine (334 kJ). PtF6 was by far the strongest oxidizer that had ever been made!
Bartlett recognized that Xe has ionization energy of +1170 kJ, which is very close to the ionization energy of O2. Since Xe+ should be about the same size as O2+, the lattice energy should be about the same with Xe+ in the cation site of the O2+PtF6- structure. Since all of the other terms in the Born-Haber cycle for the reaction of Xe with PtF6 are the same, Bartlett concluded that Xe+PtF6-, like O2+PtF6-, should be a stable compound. He purchased a lecture bottle of xenon gas and reacted the two compounds, producing an orange solid.[7] While the product initially formed in the reaction may in fact be Xe+PtF6-, the Xe+ free radical is a powerful Lewis acid and reacts further with excess PtF6. The ultimate product of the reaction is formulated [XeF+][Pt2F11-], a salt which contains Xe in the +2 oxidation state and Pt in the +5 oxidation state. This was an important discovery because it shattered the dogmatic notion, which derived from the octet rule, that elements in group VIII could not form bonds with other elements. The name of this group was changed from the "inert gases" to the "noble gases." Subsequently, many compounds of Xe and a few of Kr and even Ar (which is much harder to oxidize) were synthesized and characterized.
9.7 Stabilization of high and low oxidation states
[edit | edit source]Lattice energies, in addition to guiding the discovery of unknown compounds, are useful in explaining the absence (i.e., the thermodynamic instability) of non-existent compounds.[8] For example, CuF and AuF are unknown compounds, whereas CuF2, AuF3, and AuF5 are stable. In contrast AgF is a known, stable compound.
From the Born Haber cycle for CuF, the compound should be marginally stable (ΔHfo = -140 kJ/mol) with respect to the elements. Why then is CuF unknown?
To gain insight into this question, we first construct a Born-Haber cycle for the formation of CuF2 from the elements. This compound is stable with respect to the elements by -368 kJ/mol.

Combining the two cycles we see that the disproportionation of CuF to Cu and CuF2 is spontaneous. From similar cycles, we can also predict that the reaction 3AuF → AuF3 + 2Au should be spontaneous.

Why is the lowest oxidation state unstable for these fluorides? The key point is that the large difference in EL values (2908-972=1926 kJ in the case of copper fluorides) drives their disproportionation reactions. Note that when we use the Kapustinskii equation, we calculate that EL for CuF2 is approximately three times that of CuF. We use the same univalent radii in both calculations, but Cu has a 2+ charge in CuF2 (doubling the lattice energy relative to CuF), and contains 3/2 as many ions. The product z+z-n is thus three times larger for CuF2. The difference in EL values will thus increase as EL for the monovalent salt increases. We know that fluorides, having a small anion radius, will give larger EL values than iodides, which have larger anions. Thus the disproportionation reaction becomes more favorable for CuF than it is for CuI.
The stability of the lower vs. higher oxidation state thus depends on the size of the anion. For example, in fluorides, CuF is unstable but CuF2 is stable. However, in iodides, CuI is stable whereas CuI2 is unstable. From this we can develop a broad conclusion: small anions (O,F) tend to stabilize higher oxidation states, whereas large anions (S, Br, I...) stabilize lower oxidation states. Note that this trend has to do with the size and not with the electronegativity of the anion. Coincidentally, F and O are electronegative elements, but it is really their small size that has consequences for the lattice energy and their stabilization of higher oxidation states.
Remember that the hard-soft acid-base rules could be interpreted in terms of the dominance of ionic vs. covalent interactions. Here we have put the hard-hard interaction in quantitative terms, based on (electrostatic) lattice energies.
Ag appears to buck the periodic trend. Why is AgF stable? This is because the second IP is very high (2071 kJ vs. 1958 kJ for Cu, 1979 for Au). Thus both AgF and AgF2 are known fluorides of Ag.
9.8 Alkalides and electrides
[edit | edit source]
Another interesting consequence of lattice energies involves the formation of certain salts containing Na- and e- anions. These compounds are known as alkalides and electrides, respectively.[9] Most of these compounds have been discovered by Prof. James Dye at Michigan State University.
The alkali metals have one electron in their valence shell. For example, the electronic configurations of Na and K are [Ar]3s1 and [Kr]4s1, respectively. Although we are accustomed to seeing these very electropositive elements give up their electrons when they make compounds with electronegative elements, they can also gain an electron to achieve a [noble gas]ns2 configuration. This is possible with strong electron donors such as alkali metals, especially when the cation that is formed is stabilized by coordination to a crown ether. Typically, these compounds are synthesized by combining the alkali metal and the appropriate crown ether in liquid ammonia, and then evaporating the ammonia.
Electride salts are formed under similar conditions, except in this case the anion is simply an electron that exists in an anion "cavity" in the crystal. The crystal structures are clearly salt-like, with the cations (alkali cations stabilized by crown or cryptand ligands) alternating in the structure with electrons.


Complexing Na+ (K+, Rb+, Cs+) with crown ether ligands stabilizes the M+ form of the metal ("salt" form). Because the metal cation with its ligand shell is rather large, the lattice energy of these salts is rather low.
Solutions of electride salts are powerful reducing agents, as demonstrated by their use in the Birch reduction, in which aromatic compounds are hydrogenated to produce dienes. Electrides are also useful for reducing metal ions to metals. Evaporation of blue electride solutions in anhydrous ammonia affords a mirror of Na. Such solutions slowly lose their color as the electrons reduce ammonia to the amide anion:
- [Na(NH3)6]+e− + NH3 → NaNH2 + H2
It is interesting to consider, in the context of lattice energies and Born-Haber cycles, what might happen without these ligands present. That is, we can ask the question of whether sodium metal would prefer to exist in the metallic form as Na(s), or to form the sodide salt Na+Na-, or the electride salt Na+ e-. Of course, we already know the answer to this question. Elemental sodium is clearly a metal (it is shiny, conducts electricity, and has a bcc crystal structure) and has never been observed in either of the "salt" forms. But how far away are these forms energetically?
We can calculate the energetics by assuming that the Na- ion is about the same size as Br-, and that the e- anion is about the same size as Cl-. Then the lattice energies in the cycles become the same as those of NaBr and NaCl:
The rather surprising result from these calculations is that sodium would be marginally stable as a sodide salt and very stable (by 161 kJ) as an electride. All the terms in these simple cycles are known precisely. But we must be doing something wrong here, because Na(s) is clearly metallic.
The key, subtle point here is that Born-Haber cycles consider only the potential energy (rather than the total energy) of the substances in the cycle. Normally we can ignore the kinetic energy part of the total energy, but in this case we cannot because of the quantum mechanical effect of resonance.
9.9 Resonance energy of metals
[edit | edit source]
The solution to the problem above must consider the quantum mechanical nature of the electron. The valence electrons in Na metal are in orbitals that are delocalized over the entire crystal. However in the Na+ e- "salt" form, the electrons are localized on specific anion sites. This localization imparts an additional kinetic energy (via the "particle in a box" effect) that adds to the total energy. From the quantum mechanical result for a particle in a one-dimensional box, we obtain
where:
h = Plank's constant = 6.626 x 10-34 J s
n = energy level, assumed to be the lowest, n = 1
m = electron mass = 9.109 x 10-31 kg
L = size of the box
If we approximate the size of the electron "box" as 3 Å (3 x 10-10 m), we obtain:
This extra kinetic energy makes the Na+e- "salt" unstable relative to the electron-delocalized metal.
The calculation is not very accurate because the electron kinetic energy is not zero in the metal, and because the "box" size is not so well defined. However, it does illustrate that electron delocalization has a substantial effect in thermodynamically stabilizing metals. The situation is entirely analogous to the stabilization of aromatic molecules by electron delocalization. In molecules like benzene, resonance is also a quantum-mechanical kinetic energy effect. In general, the resonance stabilization energy is significantly larger in metals than it is in π-delocalized organic molecules. For example, the resonance energy of the six π-electrons in benzene is approximately 151 kJ/mol, less than half of the value we have calculated (per electron) in sodium metal.

Interestingly, several of the alkali metals (and other metallic elements) transform at ultrahigh pressures to optically transparent, insulating phases in which the valence electrons are localized.[10][11] These high pressure electride phases defy the general rule (which we will encounter in Chapter 10) that insulators transform to metals at sufficiently high density. They illustrate how the stable structure of an element can depend on the trade-off between the lattice energy of an ionic electride structure and the resonance energy of an electron-delocalized metal.
In addition to the salt-like electrides that are formed by complexing alkali metals with crown ether ligands, there are a number of recently discovered solid state nitrides and oxides, such as Ca2N and Ca24Al28O64, that are more properly formulated as electrides, i.e. as [Ca2N+](e-)[12] and [Ca24Al28O64]4+(e−)4.[13] In these compounds the Ca, Al, O, and N atoms have their ordinary octet oxidation states (+2, +3, -2, and -3, respectively), and electrons act as anions, filling in cage-like voids or layers in the crystal. For example, Ca2N adopts the anti-CdCl2 structure, as shown at the right, with void spaces between layers that are occupied by a 2D gas of electrons. Like other layered materials, Ca2N can be easily delaminated into thin nanosheets while retaining its structure and properties as an electride.[14] These compounds are powerful reducing agents and also have interesting activity as catalysts.[15]
9.10 The strange case of the alkali oxides
[edit | edit source]

Unexpected stoichiometry. The alkali oxides, made by reacting alkali metals (Li, Na, K, Rb, Cs) with oxygen, show an unusual trend. When lithium reacts with oxygen we obtain the binary oxide Li2O, as expected from combining an element in group I with one in group VI. Curiously, the oxide that forms most readily when sodium metal is oxidized is not Na2O, but is instead the peroxide Na2O2, which we can formulate as (Na+)2(O22-). With potassium, rubidium, and cesium we obtain the superoxides MO2, which contain the superoxide radical anion (O2-.) and should be formulated as (M+)(O2-). While it is possible to make Na2O, K2O, Rb2O, and Cs2O by reaction of the appropriate metal nitrate (MNO3) with elemental alkali metal M,[16] it is curious that these "normal valent" compounds do not form by direct reaction of the metal with oxygen.
Because the alkali metals are all very electropositive (χ = 0.8-1.0), and oxygen is very electronegative (χ = 3.5), we expect all the compounds we make by combining them to be reliably ionic. Consistent with this picture we find that Li2O (along with Na2O, K2O, and Rb2O) adopts the antifluorite structure (8:4 coordination - see problem 8.8.2), which we expect to find with relatively ionic M2X compounds. Strangely however, Cs2O crystallizes in the anti-CdCl2 structure. This is odd because CdCl2 has a layered structure that we normally associate with polar covalent MX2 compounds (see section 8.4). In Cs2O, six Cs+ cations surround each O2- anion in an octahedron. Each Cs+ is coordinated to three O2- ions, and the Cs+ ions contact each other across a van der Waals gap. The juxtaposition of Cs+ ions near each other is clearly electrostatically unfavorable, so why does Cs2O prefer the anti-CdCl2 structure to antifluorite?
The answer has to do with the crowding of alkali ions around oxygen, as illustrated for K2O at the right. Because eight large K+ ions surround each O2- ion in the structure, the cations are essentially in contact. Indeed, the metal-oxygen bonds are "stretched" in Na2O, K2O, and Rb2O relative to M-O bonds with the same bond order in other structures.[17] The situation is so extreme for Cs2O that it finds an (electrostatically unfavorable) structure in which the coordination is lowered to 6:3. This packing problem is relieved somewhat in the peroxides, where the coordination is still 8:4 but the anion is larger, and especially in the superoxides where the cation:anion ratio is 1:1 and the coordination is 6:6. Thus the larger alkali ions (K+, Rb+, Cs+) tend to form superoxides.
Another way that we can rationalize this trend is through the energetics of forming the oxides, peroxides, and superoxides.
Let's calculate the enthalpy change (per mole of metal) for forming a metal oxide M2O from the metal and oxygen:
- M(s) + 1/4 O2(g) --> 1/2 M2O(s)
We can use Hess' law to write this as a sum of reactions:
| Reaction | ΔH |
|---|---|
| M(s) --> M(g) --> M+(g) | ΔHs + IE = ΔHf,M+(g) |
| 1/4 O2(g) --> 1/2 O(g) --> 1/2 O2-(g) | 1/4 ΔHd + 1/2 EA1 + 1/2 EA2 = 1/2 ΔHf,O2-(g) |
| M+(g) + 1/2 O2-(g) --> 1/2 M2O(s) | 1/2 EL,M2O - 3/2 RT |
| Overall: | |
| M(s) + 1/4 O2(g) --> 1/2 M2O(s) | ΔHf,M+(g) + 1/2 ΔHf,O2-(g) + 1/2 EL,M2O - 3/2 RT |
To get the enthalpy change for the overall reaction (the heat of formation of 1/2 mole of M2O) we will need the heats of formation of M+(g) and O2-(g), which are available from tabulated values, and EL, which we can calculate from Kapustinskii's equation.
Similarly, we can write for the formation of the alkali peroxides:
- M(s) + 1/2 O2(g) --> 1/2 M2O2(s)
| Reaction | ΔH |
|---|---|
| M(s) --> M(g) --> M+(g) | ΔHf,M+(g) |
| 1/2 O2(g) --> 1/2 O22-(g) | 1/2 ΔHf,O22-(g) |
| M+(g) + 1/2 O22-(g) --> 1/2 M2O2(s) | 1/2 EL,M2O2 - 3/2 RT |
| Overall: | |
| M(s) + 1/2 O2(g) --> 1/2 M2O2(s) | ΔHf,M+(g) + 1/2 ΔHf,O22-(g) + 1/2 EL,M2O2 - 3/2 RT |
and for the superoxides:
- M(s) + O2(g) --> MO2(s)
| Reaction | ΔH |
|---|---|
| M(s) --> M(g) --> M+(g) | ΔHf,M+(g) |
| O2(g) --> O2-(g) | ΔHf,O2-(g) |
| M+(g) + O2-(g) --> MO2(s) | EL,MO2 - 2 RT |
| Overall: | |
| M(s) + O2(g) --> MO2(s) | ΔHf,M+(g) + ΔHf,O2-(g) + EL,MO2 - 2 RT |
For the gaseous anions and cations, we have the following heats of formation and ionic radii (CN=6):
| Ion | ΔHf, kJ | ionic radius, Å |
|---|---|---|
| Li+ | 678 | 0.76 |
| Na+ | 602 | 1.02 |
| K+ | 506 | 1.38 |
| Rb+ | 485 | 1.52 |
| Cs+ | 473 | 1.67 |
| O2- | 500 | 1.20 |
| O22- | 519 | 1.59 |
| O2- | -88 | 1.49 |
Now using Kapustinskii's equation, we can calculate the lattice energies for each compound; these have been converted to lattice enthalpies by subtracting 2 RT or 3 RT as appropriate:
| Metal | ΔHL,M2O | ΔHL,M2O2 | ΔHL,MO2 |
|---|---|---|---|
| Li | -3,065 kJ | -2,651 kJ | -918 kJ |
| Na | -2,776 | -2,433 | -838 |
| K | -2,454 | -2,178 | -751 |
| Rb | -2,345 | -2,090 | -721 |
| Cs | -2,241 | -2,007 | -678 |
As expected, the lattice energies for M2O and M2O2 are comparable, the latter being somewhat smaller in magnitude because of the larger size of the O22- anion. The lattice energies of the superoxides, MO2, are about 1/3 those of the corresponding peroxides because both the anion and cation are singly charged, and there are only two ions per formula unit.
Now, putting it all together, we can use the lattice energies and heats of formation of the individual ions to compare the heats of formation (per mole of metal) of each of the oxides:
| Metal | 1/2 ΔHf,M2O | 1/2 ΔHf,M2O2 | ΔHf,MO2 |
|---|---|---|---|
| Li | -404 kJ | -388 kJ | -328 kJ |
| Na | -338 | -354 | -324 |
| K | -271 | -321 | -328 |
| Rb | -241 | -300 | -324 |
| Cs | -53 | -70 | -81 |
We can see that for Li, the formation of Li2O is favored over Li2O2 or LiO2 because of the very favorable lattice energy of Li2O. As the lattice energy becomes less negative with increasing cation size, the peroxide becomes the most stable at Na. For the heavier alkalis, M2O becomes quite unstable and the superoxides MO2 are the most stable. This is consistent with our observations of the chemistry of the group I oxides.

Alkali suboxides. Interestingly, the heaviest alkali metals (Rb, Cs) also form a range of suboxides, such as Rb9O2, Rb6O, Cs11O3, Cs4O, Cs7O, Cs11O3Rb, Cs11O3Rb2, and Cs11O3Rb3, in which the oxide ions are octahedrally coordinated by alkali metals. Stoichiometries that are metal-rich (e.g., Rb6O and Cs7O) are crystalline intergrowths of these clusters with alkali metals.[18] These compounds are potent reducing agents.

Metal-air batteries. The alkali oxides are quite interesting in the context of metal-air batteries because of their potential for extremely high energy storage on a mass basis. Such batteries have alkali metal (typically Li) or Zn anodes and utilize oxygen from the air at the cathode. Although lithium is the lightest and therefore the most energy-dense alkali metal, there are materials problems associated with the formation of Li dendrites when the battery is recharged, and also with the slow kinetics of the four-electron interconversion between O2(g) and 2 O2- at the cathode. For this reason, superoxide batteries are currently being studied as alternatives. The one-electron cathode reaction O2 + e- = O2- is kinetically fast, and potassium[19] and sodium[20] represent potentially viable alternatives to lithium for the anode of these air-breathing batteries. Recently, it has been shown that LiO2 can be kinetically stabilized by template growth on iridium nanoparticles, potentially opening the door to very high energy density lithium-air batteries.[21]
9.11 Lattice energies and solubility
[edit | edit source]Lattice energies can also help predict compound solubilities. Let's consider a Born-Haber cycle for dissolving a salt in water. We can imagine this as the sum of two processes: (1) the vaporization of the salt to produce gaseous ions, characterized by the lattice enthalpy, and (2) the hydration of those ions to produce the solution. The enthalpy change for the overall process is the sum of those two steps. We know that the entropy change for dissolution of a solid is positive, so the solubility depends on the enthalpy change for the overall process.
Here we need to consider the trends in both the lattice energy EL and the hydration energy EH. The lattice energy depends on the sum of the anion and cation radii (r+ + r-), whereas the hydration energy has separate anion and cation terms. Generally the solvation of small ions (typically cations) dominates the hydration energy because of the 1/r2 dependence.
For salts that contain large anions, EL doesn't change much as r+ changes. That is because the anion dominates the r+ + r- term in the denominator of the formula for EL. On the other hand, EH changes substantially with r+, especially for small cations.
As a result, sulfate salts of small divalent cations, such as MgSO4 (epsom salts), are soluble, whereas the lower hydration energy of Ba2+ in BaSO4 makes that salt insoluble (Ksp = 10-10).

For small anions, EL is more sensitive to r+, whereas EH does not depend on r+ as strongly. For fluorides and hydroxides, LiF is slightly soluble whereas CsF is very soluble, and Mg(OH)2 is insoluble whereas Ba(OH)2 is very soluble.
Putting both trends together, we see that low solubility is most often encountered when the anion and cation match well in their sizes, especially when one or both are multiply charged.

Combining all our conclusions about solubility, we note the following trends:
1) Increasing size mismatch between the anion and cation leads to greater solubility, so CsF and LiI are the most soluble alkali halides.
2) Increasing covalency leads to lower solubility in the salts (due to larger EL. For example, AgF, AgCl, AgBr, and AgI exhibit progressively lower solubility because of increasing covalency.
- AgF > AgCl > AgBr > AgI
3) Increasing the charge on the anion lowers the solubility because the increase in EL is large relative to the increase in EH.
4) Small, polyvalent cations (having large EH) make soluble salts with large, univalent anions such as I-, NO3-, ClO4-, PF6-, and acetate.
Examples: Salts of transition metal and lanthanide ions
- Ln3+: Nitrate salts are soluble, but oxides and hydroxides are insoluble.
- Fe3+: Perchlorate is soluble, but sulfate is insoluble.
5) Multiple charged anions such as O2-, S2-, PO43-, and SO42- make insoluble salts with most M2+, M3+, and M4+ metals.
9.12 Discussion questions
[edit | edit source]- Explain why lattice energy calculations are very accurate for NaCl and CaCl2, but less accurate (by about 10%) for AgCl and PbCl2. Does the Born-Mayer equation under- or overestimate the latter values?
- Fluorine is more electronegative than oxygen. However, for many transition metals, we can make higher oxidation states in oxides than we can in fluorides. For example, Mn(IV) is stable in an oxide (MnO2), but MnF4 is unstable relative to MnF3 and fluorine.[22] Can you explain this in terms of lattice energies?
9.13 Problems
[edit | edit source]1. Use lattice energies to explain why MgSO4 decomposes to magnesium oxide and SO3 at a much lower temperature than does BaSO4.
2. Solid MgO might be formulated as Mg+O- or Mg2+O2-. Use the thermochemical data below (some of which are irrelevant) and Kapustinskii's formula to determine which is more stable. The lattice constant for MgO (NaCl structure) is 4.213 Å. While the idea of an O- ion might seem strange, note that the second electron affinity of O and the second ionization potential of Mg (in the table below) are both quite endothermic.
| Reaction | ∆Ho, kJ/mol |
|---|---|
| Mg(s) = Mg(g) | 148 |
| Mg(g) = Mg+(g) + e- | 739 |
| Mg+(g) = Mg2+(g) + e- | 1,452 |
| O2(g) = 2 O(g) | 498 |
| O(g) + e- = O-(g) | -141 |
| O-(g) + e- = O2-(g) | 790 |
3. From the heat of formation of solid NH4Cl (-315 kJ/mol) and gaseous NH3 (-46), the bond dissociation energies of H2 (436) and Cl2 (244), the ionization potential of atomic hydrogen (1,311), and the electron affinity of atomic chlorine (-349), calculate the gas-phase proton affinity of NH3. The lattice energy of NH4Cl may be estimated from Kapustinskii's formula using rN-Cl = 3.50 Å.
4. Bottles of aqueous ammonia are often labeled “ammonium hydroxide.” We will test this idea by using a lattice energy calculation to determine whether the salt NH4+OH- can exist.
The heats of formation of gaseous OH- and H2O are respectively -141 and -242 kJ/mol. Assuming that NH4+ is about the same size as Rb+, and OH- about the same size as F-, using Kapustinskii's formula, ionic radii, and the NH3 proton affinity calculated in problem 3, determine whether NH4+OH- should be a stable salt relative to NH3 and H2O. At what temperature should NH4+Cl- be unstable relative to NH3 and HCl, if ΔHfo for HCl is -92 kJ/mol and ΔSo (NH4Cl --> NH3 + HCl) = 280 J/mol K?
5. Lithium metal burns in nitrogen to make the nitride Li3N. The heavier alkali metals (K, Rb, Cs) can form stable azides (MN3), but not M3N nitrides. Explain why this is so.
6. (a) Do you expect BaSO4 or MgSO4 to be more soluble in water? (b) Is LiF more soluble than LiClO4? Explain.

7. Which polymorph of ZnS (zincblende or wurzite) would you expect to be more stable on the basis of electrostatic energy?
8. Arsenic contamination of ground water is a serious problem in Bangladesh, Chile, Argentina, and other parts of the world including the western United States. Arsenic poisoning been widespread in the Ganges river delta, where tube wells bring contaminated water up from 20-100 meters below the surface. One simple treatment that has been proposed is to precipitate the arsenic by aeration of the well water, which also contains high concentrations of Fe2+. Referring to the Pourbaix diagram of arsenic at the right and the Pourbaix diagram of iron in Chapter 4, identify the iron and arsenic species that are present in aerated water at neutral pH. What insoluble compound precipitates to lower the concentration of arsenic? (Hint: which compound would have the largest lattice energy?)
9.14 References
[edit | edit source]- ↑ Pauling, Linus (1929). "The principles determining the structure of complex ionic crystals". J. Am. Chem. Soc. 51 (4): 1010–1026. doi:10.1021/ja01379a006.
- ↑ K.-I. Kobayashi, T. Kimura, H. Sawada, K. Terakura, and Y. Tokura, Room-temperature magnetoresistance in an oxide material with an ordered double-perovskite structure, Nature (1998) 395, 677-680. DOI:10.1038/27167
- ↑ E. Mooser and W. B. Pearson, On the Crystal Chemistry of Normal Valence Compounds, Acta. Cryst. 12, 1015 (1959).
- ↑ Madelung E (1918). "Das elektrische Feld in Systemen von regelmäßig angeordneten Punktladungen". Phys. Zs. XIX: 524–533.
- ↑ A. F. Kapustinskii: Lattice energy of ionic crystals, Quart. Rev. Chem. Soc. Nr. 10, 1956, pp. 283–294. DOI|10.1039/QR9561000283
- ↑ Neil Bartlett and D. H. Lohmann (March 1962). "Dioxygenyl hexafluoroplatinate (V), O2+[PtF6]−". Proceedings of the Chemical Society. London: Chemical Society (3): 115. doi:10.1039/PS9620000097.
- ↑ Bartlett, N. (June 1962). "Xenon hexafluoroplatinate (V) Xe+[PtF6]−". Proceedings of the Chemical Society. London: Chemical Society (6): 218. doi:10.1039/PS9620000197.
- ↑ W. E. Dasent, Non-Existent Compounds, J. Chem. Educ., 1963, 40, p 130, DOI: 10.1021/ed040p130
- ↑ Dye, J. L. (2003). "Electrons as Anions". Science. 301 (5633): 607–608. doi:10.1126/science.1088103. PMID 12893933.
- ↑ Ma, Y.; Eremets, M.; Oganov, A. R.; Xie, Y.; Trojan, I.; Medvedev, S.; Lyakhov, A. O.; Valle, M.; Prakapenka, V., "Transparent Dense Sodium," Nature 2009, 458, 182–183. doi:10.1038/nature07786
- ↑ M.-S. Miao and R. Hoffmann, "High Pressure Electrides: A Predictive Chemical and Physical Theory," Acc. Chem. Res. 2014, 47, 1311–1317. DOI: 10.1021/ar4002922
- ↑ K. Lee, et al., "Dicalcium nitride as a two-dimensional electride with an anionic electron layer," Nature, 2013, 494, 336–340. DOI:10.1038/nature11812
- ↑ S. Matsuishi, et al., "High-Density Electron Anions in a Nanoporous Single Crystal: [Ca24Al28O64]4+(e−)4," Science, 2003, 301, 626-629. DOI: 10.1126/science.1083842
- ↑ D. L. Druffel et al., "Experimental Demonstration of an Electride as a 2D Material," J. Am. Chem. Soc., 2016, 138, 16089–16094. DOI: 10.1021/jacs.6b10114
- ↑ Y. Inoue et al., "Highly Dispersed Ru on Electride [Ca24Al28O64]4+(e−)4 as a Catalyst for Ammonia Synthesis," ACS Catal., 2014, 4, 674–680. DOI: 10.1021/cs401044a
- ↑ Holleman, A.F.; Wiberg, E., eds. (2001). Inorganic Chemistry. San Diego: Academic Press. ISBN 978-0-12-352651-9.
- ↑ N. K. McGuire and M. O'Keeffe, "Bond lengths in alkali metal oxides," J. Solid State Chem. 1984, 54, 49-53. DOI:10.1016/0022-4596(84)90129-4
- ↑ Simon, A. ”Group 1 and 2 Suboxides and Subnitrides — Metals with Atomic Size Holes and Tunnels” Coord. Chem. Rev. 1997, 163, 253–270.doi:10.1016/S0010-8545(97)00013-1
- ↑ X. Ren and Y. Wu, "A low-overpotential potassium–oxygen battery based on potassium superoxide," J. Am. Chem. Soc. 2013, 135, 2923–2926. DOI:10.1021/ja312059q
- ↑ P. Hartmann, et al., "A rechargeable room-temperature sodium superoxide (NaO2) battery," Nature Materials 2012, 12, 228–232. DOI:10.1038/nmat3486
- ↑ J. Lu et al., "A lithium–oxygen battery based on lithium superoxide," Nature 2016, 529, 377-382. DOI:10.1038/nature16484
- ↑ K. O. Christe, "Chemical synthesis of elemental fluorine," Inorg. Chem. 1986, 25, 3721–3722. DOI: 10.1021/ic00241a001









![{\displaystyle \left[{\frac {dE}{dr}}\right]_{r=r_{o}}=0.\qquad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/47a74969c9880edb112af8fe0cc9005af781c399)











