Introduction to Inorganic Chemistry/Electronic Properties of Materials: Superconductors and Semiconductors
Chapter 10: Electronic Properties of Materials: Superconductors and Semiconductors
[edit | edit source]
In Chapter 6 we developed an energy band picture for metals, starting from atomic orbitals and building up the molecular orbitals of the solid metallic crystal. This treatment gave us a useful picture of how electrons behave in metals, moving at very fast speed between scattering events, and migrating in an electric field at a slow drift velocity. It also taught us that a metal is something with a partially filled band, meaning that the Fermi level cuts through one of its bands of orbitals. An insulator or a semiconductor has a similar band picture, except that the bands are either completely full or completely empty. In this case the Fermi level lies in the gap between fully occupied and unoccupied bands. We will see in this chapter that the properties of semiconductors (along with their useful electronic applications) depend on the addition of small amounts of impurities ("dopants") that change the position of the Fermi level, resulting in conduction by electrons or "holes."
While the band picture works well for most crystalline materials, it does not tell us the whole story of conduction in solids. That is because the band model (like MO theory) is based on a one-electron model. This was an approximation we made at the very beginning of our discussion of MO theory: we used hydrogen-like (one-electron) solutions to the Schrodinger equation to give us the shapes of s, p, d, and f atomic orbitals. In a one-electron atom, these orbitals are degenerate within a given shell, and the energy differences between, e.g., 2s and 2p orbitals arise only when we consider the energy of an electron in the field of other electrons in the atom. Moving from atoms to molecules, we made linear combinations to generate one-electron molecular orbitals (and, in solids, one-electron energy bands). But as in multi-electron atoms, life is not so simple for real molecules and solids that contain many electrons. Electrons repel each other and so their movement in molecules and in solids is correlated. While this effect is weak in a "good" metal such as sodium - where the wavefunctions are highly delocalized - it can be quite important in other materials such as transition metal oxides. Correlated electron effects give rise to metal-insulator transitions that are driven by small changes in temperature, pressure, or composition, as well as to superconductivity - the passage of current with zero resistance at low temperatures. In this chapter we will develop some simple models to understand these interesting and important electronic properties of solids.
Learning goals for Chapter 10:
- Explain the physical basis of the Hubbard and Mott models of metal-insulator transitions.
- Understand why good superconductors derive from bad metals.
- Know the structures and the periodic trends in band gaps and colors of semiconductors.
- Obtain the band gap of an intrinsic semiconductor from the temperature dependence of the conductivity.
- Predict the doping type when impurities or defects are introduced into a semiconductor.
- Correlate the band picture and Fermi level with n- or p-type doping.
- Understand the physical principles of operation of diodes, LEDs, solar cells, and FETs.
- Explain the differences in structures and electronic properties of crystalline and amorphous semiconductors.
10.1 Metal-insulator transitions
[edit | edit source]
In Chapter 6 we learned that metals and insulators not only have different electrical properties but also have very different crystal structures. Metals tend to have high coordination numbers (typically 8 or 12) whereas insulators have low coordination numbers that can be rationalized as "octet" bonding arrangements. For example, in crystalline Si or Ge (diamond structure), each atom has four nearest neighbors. There are two electrons per bond, and thus each atom has eight electrons in its valence shell. Sn, the element below Ge, exists in two different forms, one (gray tin) with the diamond structure that is a brittle narrow-gap semiconductor, and the other (white tin) with a body-centered tetragonal structure that is a malleable metal. These two forms are very close in energy, and in fact metallic white tin transforms to the brittle semiconducting gray form at low temperature. Extremely cold weather in 18th century Europe caused many tin organ pipes to break and eventually turn to dust. This transformation has been called tin blight, tin disease, tin pest or tin leprosy. The dust is actually grey tin, which lacks the malleability of its metallic cousin white tin.
Under experimentally accessible temperatures and pressures, Si and Ge are always semiconducting (i.e., insulating), and Pb is always metallic. Why is Sn different? The reason has to do with orbital overlap. Theory tells us in fact that any (and all) insulators should become metallic at high enough pressure, or more to the point, at high enough density. For most insulators, however, the pressures required are far beyond those that we can achieve in the laboratory.
How can we rationalize the transition of insulators to the metallic state? Indeed, how can we understand the existence of insulators at all?


The Hubbard Model. Let's consider a chain of a large number (N) of atoms as we did in Chapter 6. For convenience, we can say that these are atoms such as H, Na, or Cs that have one valence electron. The simple band model we developed earlier suggests that the chain should be metallic, because N atoms combine to make N orbitals, and the N valence electrons only fill the band of orbitals halfway. But this conclusion doesn't depend on the density, which creates a paradox. If atoms in the chain are very far apart, we suspect that the electrons should localize on the atoms.
A solution to this problem was proposed by J. Hubbard in 1963.[1] Hubbard considered the energy required to transfer an electron from an atom to its nearest neighbor, as shown in the picture at the right. Because each atom already has one electron (with random spin), moving an electron over by one atom requires overcoming the energy of electron-electron repulsion to make a cation-anion pair. For well-separated atoms this energy (U) is given by:
- U = IP - EA - e2/4πε0d
where IP and EA are the ionization energy and electron affinity, ε0 is the permittivity of free space, and the last term in the equation represents the coulombic attraction between the cation and the anion. For atoms such as alkali metals, U is on the order of 3–5 eV, which is much larger than the thermal energy kT. Thus we expect there to be very few anion-cation pairs at room temperature, and the chain of atoms should be insulating.
What happens when we squeeze the atoms together? In the Hubbard model, as the distance between atoms decreases, the energies of both the neutral atom states and the anion-cation states broaden into bands, each of which has a band width Δ. The lower band can accommodate exactly N electrons (not 2N as in the MO picture we developed earlier) because each orbital can only take one electron without spin-pairing. Thus for small Δ the lower band is full and the upper band is empty. However, as we continue to compress the chain, the orbital overlap becomes so strong that Δ ≈ U. At this point, the bands overlap and some of the electrons fill the anion-cation states. The chain then becomes conducting and the material is metallic.

Some materials, such as Sn and VO2, happen to have just the right degree of orbital overlap to make the Hubbard transition occur by changing the temperature or pressure. Such materials can be very useful for electrical switching, as illustrated at the right for rutile structure VO2. Most materials are far away from the transition, either on the metallic or insulating side. An interesting periodic trend that illustrates this concept can be seen among the transition metal monoxides, MO (M = Ti, V, Cr, Mn, Fe, Co, Ni), all of which have the NaCl structure. TiO and VO are metallic, because the 3d orbitals have significant overlap in the structure. However, CrO, MnO, FeO, CoO, and NiO are all insulators, because the 3d orbitals contract (and therefore Δ < U) going across the transition metal series. In contrast, the analogous sulfides (TiS, VS,....NiS) are all metallic. The sulfides have the NiAs structure, in which all the metal atoms are eclipsed along the stacking axis (the hexagonal c-axis). The short metal-metal distances along that axis result in strong orbital overlap, making Δ > U.
The Mott Model. A simpler, less atomistic model of the metal-insulator transition was formulated by Neville Mott.[3] The Mott model considers the behavior of an electron in a material as a function of the density of all the other valence electrons. We know for a one-electron hydrogen-like atom (H, Na, Cs, etc.) the Schrodinger equation contains a potential energy term:
- V(r) = -(e2/4πε0r)
This potential energy function gives rise to familiar ladder of allowed energy levels in the hydrogen atom. However, in a metal, this Coulomb potential must be modified to include the screening of nuclear charge by the other electrons in the solid. In this case there is a screened Coulomb potential:
- V(r) = -(e2/4πε0r)exp(-qr)
where q, which is the inverse of the screening length, is given by:
- q2 = 4me2(3n/π)1/3(2π/h)

Here n is the density of atoms (or valence electrons), me is the electron mass, and h is Planck's constant. At distances much larger than the screening length q-1, the electron no longer "feels" the charge on the nucleus. Mott showed that there is a critical density of electrons nc above which the valence electrons are no longer bound by individual nuclei and are free to roam the crystal. This critical density marks the transition to the metallic state, and is given by the Mott criterion:
nc1/3aH ≈ 0.26
In this equation, aH is an effective Bohr radius for the valence electrons in the low-density limit, e.g. the average orbital radius of electrons in the 6s shell of a Cs atom when computing the value for Cs metal.
The important concept from the Mott model is that the metal-insulator transition depends very strongly on the density of valence electrons. This is consistent with the orbital overlap model of Hubbard, but also more general in the sense that it does not depend on a periodic structure of atoms. The Mott model is thus applicable to such diverse systems as metal atoms dissolved in liquid ammonia, metal atoms trapped in frozen gas matrices, and dopants in semiconductors.[4] In some systems, it is possible to continuously tune the density of valence electrons with rather striking results. For example, dissolving alkali metal (Li, Na, ...) in liquid ammonia (bp -33 oC) produces a blue liquid. The solvated alkali cations and negatively charged electrons impart ionic conductivity (as in a salt solution) but not electronic conductivity to the blue liquid ammonia solution. But as the concentration of electrons increases, a reflective, bronze-colored liquid phase forms that floats over the blue phase. This bronze phase is metallic and highly conducting. Eventually, with enough alkali metal added, the entire liquid is converted to the electronically conducting bronze phase.
The electrical switching of VO2 between insulating and metallic phases (see above) can also be rationalized in terms of the Mott transition. Adding more electron density (by chemical or electric field doping) increases the concentration of valence electrons, driving the phase transition to the metallic state.

Thermodynamics and phase transitions. Thermodynamically, the metal-insulator transition is a first-order phase transition. In such a transition, the structure and properties change abruptly (think of the breakfast-to-lunch transition at McDonalds - there is just no way to get pancakes after, or hamburgers before 10:30 AM![5]). Thus in the case of Sn metal, the changes in structure (from four- to eight-coordination) and in electronic conductivity (insulator to metal) occur simultaneously. As in other first order phase transitions such as ice to water to steam, there is a latent heat associated with the transition and a discontinuity in derivative properties such as the heat capacity.
A typical phase diagram for a metal-insulator transition is shown at the right for V2O3. The octahedrally coordinated V3+ ion has a d2 electron count, so there are two unpaired spins per atom, and at low temperature the spins in the lattice order antiferromagnetically. As we learned in Chapter 8, above the Néel temperature an antiferromagnet becomes a paramagnet, which is also a Mott insulator. Increasing the pressure, or doping with electrons (e.g., by substituting some d3 Cr3+ for V3+) pushes the electron density over the Mott transition, the spins pair, and the solid becomes metallic.
10.2 Superconductors
[edit | edit source]
Superconductivity refers to the flow of electrical current in a material with zero resistance. Such materials are very important for use in electromagnets, e.g., in magnetic resonance imaging (MRI) and nuclear magnetic resonance (NMR) machines, because once the current starts flowing in the coils of these magnets it doesn't stop. Magnetic levitation using superconductors - which, below a critical field strength, are perfect diamagnets that are not penetrated by magnetic flux lines - is also potentially relevant to future technologies such as magnetically levitated trains.
The phenomenon of superconductivity, first discovered in Hg metal in 1911 by Onnes, continues to be only partially understood. It is of great interest to physicists as a macroscopic quantum phenomenon, and to chemists and materials scientists who try to make better superconductors (especially those that superconduct at higher temperatures) and devices derived from them, such as superconducting quantum interference devices (SQUIDs), which are extremely sensitive magnetometers.
Spin pairing and zero resistance. The transition from the metallic to the superconducting state is related to the quantum phenomena of Bose-Einstein condensation and superfluidity. Individual electrons have spin = 1/2, and as such are fermions (particles with half-integer spin). Because of the Pauli exclusion principle, no more than two fermions can occupy the same quantum state (such as an orbital in a molecule or a solid). The familiar consequence of this rule is the aufbau filling of orbitals with spin-paired electrons in each energy level. In contrast, particles with integer spins - which are called bosons - do not have this restriction, and any number of bosons can occupy the same quantized energy level.
Superconductivity occurs when electrons spin pair into so-called Cooper pairs, which can travel through the lattice together. The electrons in a Cooper pair, although spin-paired, have a long-distance relationship: the spatial extent of a Cooper pair is a few nanometers in cuprate superconductors, and up to one micron in low Tc superconductors such as aluminum. Because its overall spin angular momentum is zero, a Cooper pair is a boson. When the temperature is low enough, the Cooper pairs "condense" into the lowest energy level. The second lowest energy level - which is typically a few meV above the ground state - is not accessible to them as long as the energy gap is larger than the thermal energy, kT. The scattering of electrons by the lattice then becomes forbidden by energy conservation because scattering dissipates energy, and the Cooper pairs cannot change their energy state. Thus the resistance (which arises from scattering, as we learned in Ch. 6) drops abruptly to zero below Tc. However, the Cooper pairs can be broken apart when they move fast, and thus superconductors turn back into normal metals (even below Tc) above some critical current density jc. This phenomenon is also related to the critical magnetic field, Hc, that quenches superconductivity.

A trampoline for electrons. What causes electrons, which repel each other because of their negative charge, to pair up and travel together in superconductors? The mechanism - which must involve some kind of attractive interaction between electrons - is well understood for "conventional" superconductors which have relatively low transition temperatures, but is not yet known with certainty for high temperature oxide superconductors. In conventional, or BCS superconductors, the spin pairing is mediated by the lattice as shown in the figure at the left. A strong electron-lattice interaction causes a distortion in the lattice as an electron moves through. This elastic deformation is felt as an attractive force by a second electron moving in the opposite direction. This can be thought of as analogous to the interaction of two people jumping on a trampoline. The weight of the first person on the trampoline creates a "well" that attracts the second one, and they tend to move together (even if they don't like each other). Strange as this interaction seems, it is supported experimentally by isotope effects on Tc and by quantitative predictions of Tc values in conventional superconductors.

Bad metals make good superconductors. All superconductors are "normal" metals - with finite electrical resistance - above their critical transition temperature, Tc. If you ask where in the periodic table one might look for superconductors, the answer is surprising. The most conductive metals (Ag, Au, Cu, Cs, etc.) make the worst superconductors, i.e., they have the lowest superconducting transition temperatures, in many cases below 0.01 K. Conversely "bad" metals, such as niobium alloys, certain copper oxides, KxBa1-xBiO3, MgB2, FeSe, and alkali salts of C60n- anions, can have relatively high transition temperatures.
We observe that most good superconductors appear in composition space very near a metal-insulator transition. In terms of our microscopic picture, orbital overlap in superconductors is poor, just barely enough to make them act as metals (Δ ≈ U) above Tc. In the normal state, superconductors with high Tc - which can be as high as 150 K - are typically "bad" metals. An important characteristic of such metals is that the mean free path of electrons (in the normal state, above Tc) is on the order of the lattice spacing, i.e., only a few Å. In contrast, we learned in Ch. 6 that good metals such as Au, Ag, and Cu have electron mean free paths that are two orders of magnitude longer (ca. 40 nm). In a bad metal, the electron "feels" the lattice rather strongly, whereas in a good metal, the electrons are insensitive to small changes in the distance between metal atoms.

What does the band picture look like for a bad metal? The key point is that because orbital overlap is poor, the metal has a high density of states at the Fermi level. This is a universal property of high temperature superconductors and provides a clue of where to look for new and improved superconducting materials. Recall that transition elements in the middle of the 3d series (Cr, Fe, Co, Ni) were magnetic because of poor orbital overlap and weak d-d bonding. The elements below these - especially Nb, Ta, and W - have just barely enough d-d orbital overlap to be on the metallic side of the metal-insulator transition and to be "bad" metals. Carbides and nitrides of these elements are typically superconducting, with the carbon and nitrogen atoms serving to adjust the valence electron density, as illustrated in the table below.

| NbC | Mo2N | TaC | VN | NbN | TaN | Nb3Ge | |
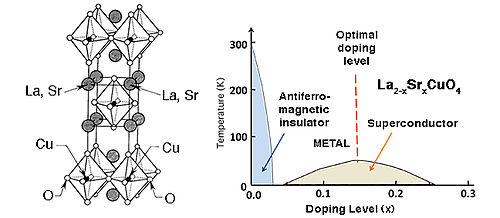
High Tc superconductors. In addition to having weak orbital overlap in the metallic state - which results in a high DOS at EF - high temperature superconductors also typically contain elements in mixed oxidation states (for example, Cu2+/3+ or Bi3+/5+) that are close in energy to the O2-/O- couple in the lattice. At ambient pressure, cuprate superconductors have the highest known Tc values, ranging between about 35 and 150 K. The crystal structures of these materials are almost all variants of the perovskite lattice, as shown at the right for the 1-2-3 superconductor YBa2Cu3O7-δ. An ideal perovskite lattice would have formula ABO3 = A3B3O9. In YBa2Cu3O7-δ, Y and Ba occupy the A cation sites, Cu occupies the B sites, and two of the nine O atoms are missing.
The YBa2Cu3O7-δ lattice consists of mixed-valent copper(II/III) oxide sheets capped by oxygen atoms to form CuO5 square pyramids. These sheets encapsulate the Y3+ cations. Copper(II) oxide ribbons that share the apical oxygen atoms of the square pyramids run in one direction through the structure. In YBa2Cu3O7-δ and related materials, one component of the structure (here the Cu-O ribbons) acts as a charge reservoir to control the doping of the planar CuO2 sheets, which are the elements of the structure that carry the supercurrent. Cuprate superconductors with Bi, Tl, or Hg-containing charge reservoir layers and multiple, eclipsed CuO2 sheets in the unit cell tend to have the highest Tc values.
The connection between the metal-insulator transtion and superconductivity is nicely illustrated in the phase diagram of La2-xSrxCuO4, the first cuprate superconductor, which was discovered in 1986 by Georg Bednorz and K. Alex Müller. This compound has a rather simple structure in which rocksalt La(Sr)O layers are intergrown with perovskite La(Sr)CuO3 layers. Undoped La2CuO4 contains only Cu2+ ions and is an antiferromagnetic insulator. As a small amount of Sr2+ is substituted for La3+, some of the Cu2+ is oxidized to Cu3+, and the lattice is doped with holes. As the doping level increases, the antiferromagnetic phase undergoes a first-order phase transition to a "bad" metal, and at slightly higher doping density the superconducting phase appears. The proximity of the superconducting phase to the metal-insulator transition is a hallmark of cuprate superconductors. A maximum Tc of 35K is observed at x = 0.15. Doping at higher levels moves the Fermi level beyond the point of highest DOS in the d-band of Cu and the superconducting phase then gradually disappears. It is interesting to compare this phase diagram with that of V2O3 (above), which also undergoes an antiferromagnetic insulator to "bad" metal transition as it is doped.
10.3 Periodic trends: metals, semiconductors, and insulators
[edit | edit source]As we consider periodic trends in the electronic properties of materials, it is important to review some of the key bonding trends we have learned in earlier chapters:
- Going down the periodic table, atoms in solids tend to adopt structures with higher coordination numbers.
- The second row of the periodic table is special, with strong s-p hybridization and π-bonding between atoms.
- Electrons in higher quantum shells are less strongly bound, so the energy difference between bonding and antibonding orbitals becomes smaller for heavier atoms.
We also know that most of the elements in the periodic table are metals, but the elements in the top right corner are insulating under ordinary conditions (1 atm. pressure) and tend to obey the octet rule in their compounds.

At the transition between metals and non-metals in the periodic table we encounter a crossover in electronic properties, as well as in other properties such as the acidity of the oxides (see Ch. 3). The group of elements at the border is loosely referred to as the metalloids. Several of these elements (such as C, Sn, and As) can exist as different allotropes that can be metals, insulators, or something in between.
A more rigorous delineation of the electronic properties of these elements (and of many compounds) can be made by considering their band structures and the temperature dependence of the electronic conductivity. As we have previously discussed, metals have partially filled energy bands, meaning that the Fermi level intersects a partially filled band. With increasing temperature, metals become poorer conductors because lattice vibrations (which are called phonons in the physics literature) scatter the mobile valence electrons. In contrast, semiconductors and insulators, which have filled and empty bands, become better conductors at higher temperature, since some electrons are thermally excited to the lowest empty band. The distinction between insulators and semiconductors is arbitrary, and from the point of view of metal-insulator transitions, all semiconductors are insulators. We typically call an insulator a semiconductor if its band gap (Egap) is less than about 3 eV. A semimetal is a material that has a band gap near zero, examples being single sheets of sp2-bonded carbon (graphene) and elemental Bi. Like a narrow gap semiconductor, a semimetal has higher conductivity at higher temperature.
10.4 Semiconductors: band gaps, colors, conductivity and doping
[edit | edit source]
Semiconductors, as we noted above, are somewhat arbitrarily defined as insulators with band gap energy < 3.0 eV (~290 kJ/mol). This cutoff is chosen because, as we will see, the conductivity of undoped semiconductors drops off exponentially with the band gap energy and at 3.0 eV it is very low. Also, materials with wider band gaps (e.g. SrTiO3, Egap = 3.2 eV) do not absorb light in the visible part of the spectrum.
There are a number of places where we find semiconductors in the periodic table:
- Early transition metal oxides and nitrides, especially those with d0 electron counts such as TiO2, TaON, and WO3
- Oxides of later 3d elements such as Fe2O3, NiO, and Cu2O
- Layered transition metal chalcogenides with d0, d2 and d6 electron counts including TiS2, ZrS2, MoS2, WSe2, and PtS2
- d10 copper and sliver halides, e.g., CuI, AgBr, and AgI
- Zincblende- and wurtzite-structure compounds of the p-block elements, especially those that are isoelectronic with Si or Ge, such as GaAs and CdTe. While these are most common, there are other p-block semiconductors that are not isoelectronic and have different structures, including GaS, PbS, and Se.
The p-block octet semiconductors are by far the most studied and important for technological applications, and are the ones that we will discuss in detail.
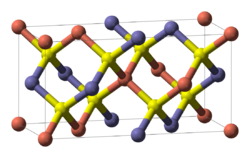
Zincblende- and wurtzite-structure semiconductors have 8 valence electrons per 2 atoms. These combinations include 4-4 (Si, Ge, SiC,…), 3-5 (GaAs, AlSb, InP,…), 2-6 (CdSe, HgTe, ZnO,…), and 1-7 (AgCl, CuBr,…) semiconductors. Other variations that add up to an octet configuration are also possible, such as CuIInIIISe2, which has the chalcopyrite structure, shown at the right.
How does the band gap energy vary with composition? There are two important trends
(1) Going down a group in the periodic table, the gap decreases:
- C (diamond) > Si > Ge > α-Sn
Egap (eV): 5.4 1.1 0.7 0.0
This trend can be understood by recalling that Egap is related to the energy splitting between bonding and antibonding orbitals. This difference decreases (and bonds become weaker) as the principal quantum number increases.
(2) For isoelectronic compounds, increasing ionicity results in a larger band gap.
- Ge < GaAs < ZnSe
- 0.7 1.4 2.8 eV
- Sn < InSb < CdTe < AgI
- 0.0 0.2 1.6 2.8 eV
This trend can also be understood from a simple MO picture, as we discussed in Ch. 2. As the electronegativity difference Δχ increases, so does the energy difference between bonding and antibonding orbitals.


The band gap is a very important property of a semiconductor because it determines its color and conductivity. Many of the applications of semiconductors are related to band gaps:
- Narrow gap materials (HgxCd1-xTe, VO2, InSb, Bi2Te3) are used as infrared photodetectors and thermoelectrics (which convert heat to electricity).
- Wider gap materials (Si, GaAs, GaP, GaN, CdTe, CuInxGa1-xSe2) are used in electronics, light-emitting diodes, and solar cells.
Semiconductor solid solutions such as GaAs1-xPx have band gaps that are intermediate between the end member compounds, in this case GaAs and GaP (both zincblende structure). Often, there is a linear relation between composition and band gap, which is referred to as Vegard's Law. This "law" is often violated in real materials, but nevertheless offers useful guidance for designing materials with specific band gaps. For example, red and orange light-emitting diodes (LED's) are made from solid solutions with compositions of GaP0.40As0.60 and GaP0.65As0.35, respectively. Increasing the mole fraction of the lighter element (P) results in a larger band gap, and thus a higher energy of emitted photons.
Colors of semiconductors. The color of absorbed and emitted light both depend on the band gap of the semiconductor. Visible light covers the range of approximately 390-700 nm, or 1.8-3.1 eV. The color of emitted light from an LED or semiconductor laser corresponds to the band gap energy and can be read off the color wheel shown at the right.
The color of absorbed light includes the band gap energy, but also all colors of higher energy (shorter wavelength), because electrons can be excited from the valence band to a range of energies in the conduction band. Thus semiconductors with band gaps in the infrared (e.g., Si, 1.1 eV and GaAs, 1.4 eV) appear black because they absorb all colors of visible light. Wide band gap semiconductors such as TiO2 (3.0 eV) are white because they absorb only in the UV. Fe2O3 has a band gap of 2.2 eV and thus absorbs light with λ < 560 nm. It thus appears reddish-orange (the colors of light reflected from Fe2O3) because it absorbs green, blue, and violet light. Similarly, CdS (Egap = 2.6 eV) is yellow because it absorbs blue and violet light.

Electrons and holes in semiconductors. Pure (undoped) semiconductors can conduct electricity when electrons are promoted, either by heat or light, from the valence band to the conduction band. The promotion of an electron (e-) leaves behind a hole (h+) in the valence band. The hole, which is the absence of an electron in a bonding orbital, is also a mobile charge carrier, but with a positive charge. The motion of holes in the lattice can be pictured as analogous to the movement of an empty seat in a crowded theater. An empty seat in the middle of a row can move to the end of the row (to accommodate a person arriving late to the movie) if everyone moves over by one seat. Because the movement of the hole is in the opposite direction of electron movement, it acts as a positive charge carrier in an electric field.
The opposite process of excitation, which creates an electron-hole pair, is their recombination. When a conduction band electron drops down to recombine with a valence band hole, both are annihilated and energy is released. This release of energy is responsible for the emission of light in LEDs.
At equilibrium, the creation and annihilation of electron-hole pairs proceed at equal rates. This dynamic equilibrium is analogous to the dissociation-association equilibrium of H+ and OH- ions in water. We can write a mass action expression:
- n×p = Keq = ni2
where n and p represent the number density of electrons and holes, respectively, in units of cm-3. The intrinsic carrier concentration, ni, is equal to the number density of electrons or holes in an undoped semiconductor, where n = p = ni.
Note the similarity to the equation for water autodissociation:
- [H+][OH-] = Kw
By analogy, we will see that when we increase n (e.g., by doping), p will decrease, and vice-versa, but their product will remain constant at a given temperature.
Temperature dependence of the carrier concentration. Using the equations Keq = exp(-ΔGo/RT) and ΔGo = ΔHo – TΔSo, we can write:
- n×p = ni2 = exp(ΔSo/R)exp(-ΔHo/RT)
The entropy change for creating electron hole pairs is given by:
- ΔSo = R ln(NC) + R ln(NV) = R ln(NCNV)
where NV and NC are the effective density of states in the valence and conduction bands, respectively.
and thus we obtain
- ni2 = NCNV exp(-ΔHo/RT)
Since the volume change is negligible, ΔHo ≈ ΔEo, and therefore ΔHo/R ≈ Egap/k, from which we obtain
- ni2 = NCNV exp(-Egap/kT)
and finally
- n = p = ni = (NCNV)1/2 exp(-Egap/2kT)
For pure Si (Egap = 1.1 eV) with N ≈ 1022/cm3, we can calculate from this equation a carrier density ni of approximately 1010/cm3 at 300 K. This is about 12 orders of magnitude lower than the valence electron density of Al, the element just to the left of Si in the periodic table. Thus we expect the conductivity of pure semiconductors to be many orders of magnitude lower than those of metals.

Conductivity of intrinsic semiconductors. The conductivity (σ) is the product of the number density of carriers (n or p), their charge (e), and their mobility (µ). Recall from Chapter 6 that µ is the ratio of the carrier drift velocity to the electric field and has units of cm2/Volt-second. Typically electrons and holes have somewhat different mobilities (µe and µh, respectively) so the conductivity is given by:
- σ = neµe + peµh
For either type of charge carrier, we recall from Ch. 6 that the mobility μ is given by:
- μ = vdrift/E = eτ/m,
where e is the fundamental unit of charge, τ is the scattering time, and m is the effective mass of the charge carrier.
Taking an average of the electron and hole mobilities, and using n = p, we obtain
- σ = σo exp(-Egap/2kT), where σo = 2(NCNV)1/2eµ.
By measuring the conductivity as a function of temperature, it is possible to obtain the activation energy for conduction, which is Egap/2. This kind of plot, which resembles an Arrhenius plot, is shown at the right for three different undoped semiconductors. The slope of the line in each case is -Egap/2k.

Doping of semiconductors. Almost all applications of semiconductors involve controlled doping, which is the substitution of impurity atoms, into the lattice. Very small amounts of dopants (in the parts-per-million range) dramatically affect the conductivity of semiconductors. For this reason, very pure semiconductor materials that are carefully doped - both in terms of the concentration and spatial distribution of impurity atoms - are needed.
n- and p-type doping. In crystalline Si, each atom has four valence electrons and makes four bonds to its neighbors. This is exactly the right number of electrons to completely fill the valence band of the semiconductor. Introducing a phosphorus atom into the lattice (the positively charged atom in the figure at the right) adds an extra electron, because P has five valence electrons and only needs four to make bonds to its neighbors. The extra electron, at low temperature, is bound to the phosphorus atom in a hydrogen-like molecular orbital that is much larger than the 3s orbital of an isolated P atom because of the high dielectric constant of the semiconductor. In silicon, this "expanded" Bohr radius is about 42 Å, i.e., 80 times larger than in the hydrogen atom. The energy needed to ionize this electron – to allow it to move freely in the lattice - is only about 40–50 meV, which is not much larger the thermal energy (26 meV) at room temperature. Therefore the Fermi level lies just below the conduction band edge, and a large fraction of these extra electrons are promoted to the conduction band at room temperature, leaving behind fixed positive charges on the P atom sites. The crystal is n-doped, meaning that the majority carrier (electron) is negatively charged.
Alternatively, boron can be substituted for silicon in the lattice, resulting in p-type doping, in which the majority carrier (hole) is positively charged. Boron has only three valence electrons, and "borrows" one from the Si lattice, creating a positively charged hole that exists in a large hydrogen-like orbital around the B atom. This hole can become delocalized by promoting an electron from the valence band to fill the localized hole state. Again, this process requires only 40–50 meV, and so at room temperature a large fraction of the holes introduced by boron doping exist in delocalized valence band states. The Fermi level (the electron energy level that has a 50% probability of occupancy at zero temperature) lies just above the valence band edge in a p-type semiconductor.
As noted above, the doping of semiconductors dramatically changes their conductivity. For example, the intrinsic carrier concentration in Si at 300 K is about 1010 cm-3. The mass action equilibrium for electrons and holes also applies to doped semiconductors, so we can write:
- n×p = ni2 = 1020 cm-6 at 300K
If we substitute P for Si at the level of one part-per-million, the concentration of electrons is about 1016 cm-3, since there are approximately 1022 Si atoms/cm3 in the crystal. According to the mass action equation, if n = 1016, then p = 104 cm-3. There are three consequences of this calculation:
- The density of carriers in the doped semiconductor (1016 cm-3) is much higher than in the undoped material (~1010 cm-3), so the conductivity is also many orders of magnitude higher.
- The activation energy for conduction is only 40–50 meV, so the conductivity does not change much with temperature (unlike in the intrinsic semiconductor)
- The minority carriers (in this case holes) do not contribute to the conductivity, because their concentration is so much lower than that of the majority carrier (electrons).
Similarly, for p-type materials, the conductivity is dominated by holes, and is also much higher than that of the intrinsic semiconductor.
Chemistry of semiconductor doping. Sometimes it is not immediately obvious what kind of doping (n- or p-type) is induced by "messing up" a semiconductor crystal lattice. In addition to substitution of impurity atoms on normal lattice sites (the examples given above for Si), it is also possible to dope with vacancies - missing atoms - and with interstitials - extra atoms on sites that are not ordinarily occupied. Some simple rules are as follows:
- For substitutions, adding an atom to the right in the periodic table results in n-type doping, and an atom to the left in p-type doping.
- For example, when TiO2 is doped with Nb on some of the Ti sites, or with F on O sites, the result is n-type doping. In both cases, the impurity atom has one more valence electron than the atom for which it was substituted. Similarly, substituting a small amount of Zn for Ga in GaAs, or a small amount of Li for Ni in NiO, results in p-type doping.
- Anion vacancies result in n-type doping, and cation vacancies in p-type doping.
- Examples are anion vacancies in CdS1-x and WO3-x, both of which give n-type semiconductors, and copper vacancies in Cu1-xO, which gives a p-type semiconductor.
- Interstitial cations (e.g. Li) donate electrons to the lattice resulting in n-type doping. Interstitial anions are rather rare but would result in p-type doping.
Sometimes, there can be both p- and n-type dopants in the same crystal, for example B and P impurities in a Si lattice, or cation and anion vacancies in a metal oxide lattice. In this case, the two kinds of doping compensate each other, and the doping type is determined by the one that is in higher concentration. A dopant can also be present on more than one site. For example, Si can occupy both the Ga and As sites in GaAs, and the two substitutions compensate each other. Si has a slight preference for the Ga site, however, resulting in n-type doping.
10.5 Semiconductor p-n junctions
[edit | edit source]
Semiconductor p-n junctions are important in many kinds of electronic devices, including diodes, transistors, light-emitting diodes, and photovoltaic cells. To understand the operation of these devices, we first need to look at what happens to electrons and holes when we bring p-type and n-type semiconductors together.
At the junction between the two materials, mobile electrons and holes annihilate each other, leaving behind the fixed + and - charges of the electron donor and electron acceptor dopants, respectively. For example, on the n-side of a silicon p-n junction, the positively charged dopants are P+ ions and on the p-side the negatively charged dopants are B-. The presence of these uncompensated electrical charges creates an electric field, the built-in field of the p-n junction. The region that contains these charges (and a very low density of mobile electrons or holes) is called the depletion region.
The electric field, which is created in the depletion region by electron-hole recombination, repels both the electrons (on the n-side) and holes (on the p-side) away from the junction. The concentration gradient of electrons and holes, however, tends to move them in the opposite direction by diffusion. At equilibrium, the flux of mobile carriers is zero because the field-driven migration flux is equal and opposite to the concentration-driven diffusion flux.
The width of the depletion layer depends on the screening length in the semiconductor, which in turn depends on the dopant density. At high doping levels, the depletion layer is narrow (tens of nanometers across), whereas at low doping density it can be as thick as 1 µm. The depletion region is the only place where the electric field is nonzero, and the only place where the bands bend. Elsewhere in the semiconductor the field is zero and the bands are flat.
In the middle of a p-n junction, the Fermi level energy, EF, is halfway between the valence band, VB, and the conduction band, CB, and the semiconductor is intrinsic (n = p = ni)
10.6 Diodes, LEDs and solar cells
[edit | edit source]
Diodes are semiconductor devices that allow current to flow in only one direction. Diodes act as rectifiers in electronic circuits, and also as efficient light emitters (in LEDs) and solar cells (in photovoltaics). The basic structure of a diode is a junction between a p-type and an n-type semiconductor, called a p-n junction. Typically, diodes are made from a single semiconductor crystal into which p- and n- dopants are introduced.
If the n-side of a diode is biased at positive potential and the p-side is biased negative, electrons are drawn to the n-side and holes to the p-side. This reinforces the built in potential of the p-n junction, the width of the depletion layer increases, and very little current flows. This polarization direction is referred to as "back bias." If the diode is biased the other way, carriers are driven into the junction where they recombine. The electric field is diminished, the bands are flattened, and current flows easily since the applied bias lowers the built-in potential. This is called "forward bias."


The figure on the left illustrates a forward-biased diode, through which current flows easily. As electrons and holes are driven into the junction (black arrows in lower left figure), they recombine (downward blue arrows), producing light and/or heat. The Fermi level in the diode is indicated as the dotted line. There is a drop in the Fermi level (equal to the applied bias) across the depletion layer. The corresponding diode i-V curve is shown on the right. The current rises exponentially with applied voltage in the forward bias direction, and there is very little leakage current under reverse bias. At very high reverse bias (typically tens of volts) diodes undergo avalanche breakdown and a large reverse current flows.

A light-emitting diode or LED is a kind of diode that converts some of the energy of electron-hole recombination into light. This radiative recombination process always occurs in competition with non-radiative recombination, in which the energy is simply converted to heat. When light is emitted from an LED, the photon energy is equal to the bandgap energy. Because of this, LED lights have pure colors and narrow emission spectra relative to other light sources, such as incandescent and fluorescent lights. LED lights are energy-efficient and thus are typically cool to the touch.
Direct-gap semiconductors such as GaAs and GaP have efficient luminescence and are also good light absorbers. In direct gap semiconductors, there is no momentum change involved in electron-hole creation or recombination. That is, the electrons and holes originate at the same value of the momentum wavevector k, which we encountered in Ch. 6. k is related to the momentum (also a vector quantity) by p = hk/2π. In a direct-gap semiconductor, the top of the valence band and the bottom of the conduction band most typically both occur at k = 0. Since the momentum of the photon is close to zero, photon absorption and emission are strongly allowed (and thus kinetically fast). Polar semiconductors such as GaAs, GaN, and CdSe are typically direct-gap materials. Indirect-gap semiconductors such as Si and Ge absorb and emit light very weakly because the valence band maximum and conduction band minimum do not occur at the same point in k-space. This means that a lattice vibration (a phonon) must also be created or annihilated in order to conserve momentum. Since this "three body" (electron, hole, phonon) process has low probability, the radiative recombination of electrons and holes is slow relative to non-radiative decay - the thermalization of electron-hole energy as lattice vibrations - in indirect-gap semiconductors. The momentum selection rule thus prevents light absorption/emission and there are no pure Si LEDs or Si-based lasers.
While red, orange, yellow, and green LEDs can be fabricated relatively easily from AlP-GaAs solid solutions, it was initially very difficult to fabricate blue LEDs because the best direct gap semiconductor with a bandgap in the right energy range is a nitride, GaN, which is difficult to make and to dope p-type. Working at Nichia Corporation in Japan, Shuji Nakamura succeeded in developing a manufacturable process for p-GaN, which is the basis of the blue LED. Because of the importance of this work in the development of information storage (Blu-Ray technology) and full-spectrum, energy-efficient LED lighting, Nakamura shared the 2014 Nobel Prize in Physics with Isamu Asaki and Hiroshi Amano, both of whom had made earlier contributions to the development of GaN diodes.

A Solar cell, or photovoltaic cell, converts light absorbed in a p-n junction directly to electricity by the photovoltaic effect. Photovoltaics is the field of technology and research related to the development of solar cells for conversion of solar energy to electricity. Sometimes the term solar cell is reserved for devices intended specifically to capture energy from sunlight, whereas the term photovoltaic cell is used when the light source is unspecified.


Photocurrent in p-n junction solar cells flows in the diode reverse bias direction. In the dark, the solar cell simply acts as a diode. In the light, the photocurrent can be thought of as a constant current source, which is added to the i-V characteristic of the diode. The relationship between the dark and light current in a photovoltaic cell is shown in the diagram at the left.
The built-in electric field of the p-n junction separates e- h+ pairs that are formed by absorption of bandgap light in the depletion region. The electrons flow downhill, towards the n-type side of the junction, the holes flow uphill towards the p-side. If hν ≥ Egap, light can be absorbed by promoting an electron from the valence band to the conduction band. Any excess energy is rapidly thermalized. Light with hν > Eg thus can store only Eg worth of energy in an e- h+ pair. If light is absorbed outside of depletion region, i.e., on the n- or p-side of the junction where there is no electric field, minority carriers must diffuse into the junction in order to be collected. This process occurs in competition with electron-hole recombination. Because impurity atoms and lattice defects make efficient recombination centers, semiconductors used in solar cells (especially indirect-gap materials such as Si, which must be relatively thick in order to absorb most of the solar spectrum) must be very pure. Most of the cost of silicon solar cells is associated with the process of purifying elemental silicon and growing large single crystals from the melt.
In the photodiode i-V curve above, Vphoto is typically only about 70% of the bandgap energy Egap. The photocurrent is limited by the photon flux, the recombination rate, and the re-emission of absorbed light.[6] The area of the orange rectangle indicates the power generated by the solar cell, which can be calculated as P = i x V. In good single crystal or polycrystalline solar cells made of Si, GaAs, CdTe, CuInxGa1-xSe2, or (CH3NH3)PbI3 the quantum yield (the ratio of short circuit photocurrent to photon flux) is close to unity.
Solar cells have many current applications. Individual cells are used for powering small devices such as electronic calculators. Photovoltaic arrays generate a form of renewable electricity, particularly useful in situations where electrical power from the grid is unavailable such as in remote area power systems, Earth-orbiting satellites and space probes, remote radio-telephones and water pumping applications. Photovoltaic electricity is also increasingly deployed in grid-tied electrical systems.

The cost of installed photovoltaics (calculated on a per-watt basis) has dropped over the past decade at a rate of about 13% per year, and has already reached grid parity in Germany and a number of other countries.[7] Photovoltaic grid parity was anticipated in U.S. power markets in the 2020 timeframe.[8] [9]A major driver in the progressively lower cost of photovoltaic power is the steadily increasing efficiency of solar cells, which is shown in the graphic at the right. Higher efficiency solar cells require less area to deliver the same amount of power, and this lowers the "balance of system" costs such as wiring, roof mounting, etc., which scale as the area of the solar panels. Progress towards higher efficiency reflects improved processes for making photovoltaic materials such as silicon and gallium arsenide, as well as the discovery of new materials. Silicon solar cells are a mature technology, so they are now in the flat part of the learning curve and are approaching their maximum theoretical efficiencies. Newer technologies such as organic photovoltaics, quantum dot solar cells, and lead halide perovskite cells are still in the rising part of the learning curve.
A field effect transistor (FET) is a transistor that uses an electric field to control the width of a conducting channel and thus the current in a semiconductor material. It is classified as unipolar transistor, in contrast to bipolar transistors.

Field effect transistors function as current amplifiers. The typical structure of Si-based FETs is one in which two n-type regions (the source and the drain) are separated by a p-type region. An oxide insulator over the p-type region separates a metal gate lead from the semiconductor. This structure is called a metal-oxide-semiconductor FET (or MOSFET). When voltage is applied between source and drain, current cannot flow because either the n-p or the p-n junction is back-biased. When a positive potential is applied to the gate, however, electrons are driven towards the gate, and locally the semiconductor is "inverted" to n-type. Then the current flows easily between the n-type source and drain through the n-channel. The current flow between the source and drain is many times larger than the current through the gate, and thus the FET can act as an amplifier. Current flow can also represent a logical "1," so FETs are also used in digital logic.
In electronic devices such as microprocessors, field-effect transistors are kept in the off-state most of the time in order to minimize background current and power consumption. The FET shown above, which has n-type source and drain regions, is called an NMOS transistor. In a PMOS transistor, the source and drain regions are p-type and the gate is n-type. In CMOS (complementary metal-oxide semiconductor) integrated circuits, both NMOS and PMOS transistors are used. CMOS circuits are constructed in such a way that all PMOS transistors must have either an input from the voltage source or from another PMOS transistor. Similarly, all NMOS transistors must have either an input from ground or from another NMOS transistor. This arrangement results in low static power consumption.

Transistors are most useful in the range of gate voltage (indicated by the red circle in the figure at the left) where the source-drain current changes rapidly. In this region it is possible to effect a large change in current between source and drain when a small signal is applied to the gate. An important figure of merit for FETs is the subthreshold slope, which is the slope a plot of log(current) vs. Vgate. An ideal subthreshold slope is one decade of current per 60 mV of gate bias. Typically, a decade change in source-drain current can be achieved with a change in gate voltage of ~70 mV. The performance of FETs as switches and amplifiers is limited by the subthreshold slope, which in turn is limited by the capacitance of the gate. It is desirable to have a very high gate capacitance, which requires a thin insulating oxide, but also to have a small leakage current, which requires a thick oxide. A current challenge in the semiconductor industry is to continue to scale FETs to even smaller nanoscale dimensions while maintaining acceptable values of these parameters. This is being done by developing new gate insulator materials that have higher dielectric constants than silicon oxide and do not undergo redox reactions with silicon or with metal gate leads. Only a few known materials (such as hafnium oxynitride and hafnium silicates) currently meet these stringent requirements.
10.7 Amorphous semiconductors
[edit | edit source]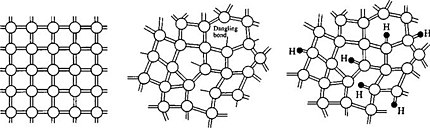

Amorphous semiconductors are disordered or glassy forms of crystalline semiconductor materials. Like non-conducting glasses, they are network structures with primarily covalent bonding. Crystalline silicon, which has the diamond structure, is an ordered arrangement of fused six-membered silicon rings, all in the "chair" conformation, as we saw in Ch. 8. The local bonding environment of the silicon atoms is tetrahedral. The silicon atoms in amorphous silicon (a-Si) are also predominantly tetrahedrally coordinated, but there is no long-range order in the structure. In addition to six-membered rings, there are five- and seven-membered rings, as well as some "dangling bond" sites in which Si atoms have only three nearest neighbors.
Two of the most widely studied amorphous semiconductors are a-Si and amorphous selenium, a-Se. Si and Se can both be made in glassy form, usually by sputtering or evaporation at relatively low temperature. In a-Se, as in a-Si, locally, most of the atoms have their "normal" valence, but there are many defects and irregularities in the structure. Dangling bonds in amorphous semiconductors have orbital energies in the middle of gap, and electrons in these states are effectively non-bonding. Because these dangling bond sites are far apart from each other, there is little orbital overlap between them, and they also exist over a range of energies. Electrons in these mid-gap states are therefore localized, a phenomenon known as Anderson localizaton. Amorphous Si is insulating because electrons the Fermi level (in the middle of the gap) are not mobile in the lattice. These localized states create a mobility gap, and only electrons in states that are strongly bonding or antibonding are delocalized. Therefore, unmodified a-Si is not very useful as a semiconductor. However, by hydrogenating the material as it is formed (typically in a plasma of H atoms), the under-coordinated Si atoms are bonded to hydrogen atoms. This generates filled bonding and empty antibonding orbitals, the energies of which are outside the mobility gap. Hydrogenation thus lowers the density of states in the mobility gap. Hydrogenated amorphous silicon (a-Si:H) is insulating in the dark, but is a good photoconductor because light absorption creates electrons and holes in mobile states that are outside the mobility gap.



The photoconductivity of amorphous Se is exploited in xerography. A conductive drum coated with a-Se, which is insulating, is charged with static electricity by corona discharge from a wire. When the drum is exposed to a pattern of light and dark (the image to be duplicated), the illuminated a-Se areas become conductive and the static charge is dissipated from those parts of the drum. Carbon-containing toner particles then adhere via static charge to the areas that were not exposed to light, and are transferred and bonded to paper to make the copy. The speed of the process and the high resolution of pattern transfer depend on the very low conductivity of a-Se in the dark and its high conductivity under illumination.
Amorphous hydrogenated Si is used in inexpensive thin film solar cells. The mobility gap is about 1.7 eV, which is larger than the bandgap crystalline of Si (1.1 eV). a-Si:H is a direct-gap material, and therefore thin films are good light absorbers. a-Si:H solar cells can be vapor-deposited in large-area sheets. p+Si-a-Si:H-n+Si cells have around 10% power conversion efficiency. However amorphous Si solar cells gradually lose efficiency as they are exposed to light. The mechanism of this efficiency loss, called the Staebler-Wronski effect,[10], involves photogenerated electron-hole pairs which have sufficient energy to cause chemical changes in the material. While the exact mechanism is still unclear, it has been proposed that the energy of electron-hole recombination breaks a weak Si-Si bond, and that one of the resulting dangling bonds abstracts a H atom, leaving a passivated Si-H center and a permanent dangling bond. The effect is minimized by hydrogenating a-Si and can be partially reversed by annealing.
Thin layers of amorphous silicon are used in conjunction with crystalline silicon in heterojunction intrinsic thin-layer (HIT) solar cells.[11] Because the mobility gap of a-Si is wider than the bandgap of c-Si, there is a potential energy barrier at the amorphous-crystalline interface that reflects electrons and holes away from that interface. At the p+ contact, only holes can tunnel through the barrier, whereas only electrons can tunnel through the barrier to the n+ contact. The passivation of surface defects that are sites of electron-hole recombination prevents a major loss mechanism in solar cells, increasing both the photovoltage and the photocurrent relative to conventional c-Si p-n junction cells. Panasonic and Sanyo have announced the production of HIT cells with power conversion efficiencies as high as 23%.
10.8 Discussion questions
[edit | edit source]- How is magnetic ordering in the 3d transition metals (Fe, Co, Ni) and the absence of magnetism in the elements just below them (Ru, Ir, Pd) related to the metal-insulator transition?
- Why are good metals bad superconductors and vice-versa?
- Discuss why semiconducting oxides of early transition metals such as TiO2 and Nb2O5 can be doped n-type but not p-type. Conversely, semiconducting late transition metal oxides such as NiO and Cu2O can be doped p-type but not n-type.
10.9 Problems
[edit | edit source]
1. The structure of a high temperature superconductor containing barium, europium, copper, and oxygen is shown at the right. What are the coordination environments of Cu in this compound? This structure is actually closely related to perovskite, ABO3. Explain the relationship between this structure and the ideal perovskite structure.
2. VO2 can exist in insulating or metallic form, depending on temperature and pressure. Which form would be stabilized by increasing the temperature? Explain your answer.

3. Explain briefly how and why the bandgaps for octet p-block semiconductors vary (1) with the average principal quantum number, and (2) with the electronegativity difference between anion and cation.
4. Indicate the type of conduction (n or p) in the following: (a) Se-doped GaAs, (b) InAs1-x, where x << 1, (c) Li0.05Ni0.95O, (d) LixWO3, where x << 1.
5. The structure of copper indium selenide, a semiconductor used in thin film solar cells, is shown at the right in sections.
(a) What is the stoichiometry of the compound?
(b) What kind of doping (n or p) will occur if a small amount of iodine is substituted for selenium?
(c) What kind of doping (n or p) will occur if a small fraction of the indium sites are occupied by copper atoms?

6. The relationship between band gap and the wavelength of light absorbed is lambda (nm) = 1240/Eg (eV). Predict the colors of anatase TiO2 (Eg = 3.1 eV), SiC (2.0 eV), ZnSnP2 (1.7 eV), ZnGeP2 (1.9 eV), and InP (1.27 eV). In other words, what color do they appear to the eye?
7. The conductivity of a certain intrinsic (undoped) semiconductor increases by a factor of two when the temperature is raised from 300 to 330 K. What is the bandgap (in eV)? R = 8.314 J/mol-K, 1 eV/atom = 96.52 kJ/mole.
8. Pure Ge is much more conductive than pure Si. Given their bandgaps (0.74 and 1.15 eV, respectively), estimate the ratio of their conductivities at room temperature.
9. The figure at the right illustrates the trends in conductivity vs. inverse temperature for Si, Ge, and As-doped Ge. Identify lines (i), (ii), and (iii) with the appropriate materials. Explain why the slope of line (i) is close to zero.
10. Sketch a silicon p-n junction, showing the depletion region, band bending, and the Fermi level in the absence of light or applied potential. In the dark, the p-n junction acts as a rectifier. (a) Which way do electrons and holes flow most easily in the dark? (b) Does the built in electric field increase or decrease under forward bias? (c) In the light, the junction acts as a photodiode. In this case, under short circuit conditions, do electrons flow in the same direction or in the opposite direction as in (a)? Explain.
10.10 References
[edit | edit source]- ↑ Hubbard, J. (1963). "Electron Correlations in Narrow Energy Bands". Proceedings of the Royal Society of London. 276 (1365): 238–257. Bibcode:1963RSPSA.276..238H. doi:10.1098/rspa.1963.0204. JSTOR 2414761.
- ↑ T. Mizokawa, Metal-insulator transitions: orbital control, Nature Physics 9, 612–613 (2013), doi: doi:10.1038/nphys2769
- ↑ N. F. Mott, (1961) "The Transition to the Metallic State," Phil. Mag. 6, 287. DOI: 10.1080/14786436108243318.
- ↑ P. P. Edwards and M. J. Sienko (1982) "The Transition to the Metallic State," Acc. Chem. Res. 15, 87-93. DOI: 10.1021/ar00075a004
- ↑ Recent data have disproven this assertion; MacDonalds has finally responded to public opinion and is offering breakfast after 10:30 AM. But the laws of thermodynamics remain immutable and eternal
- ↑ E. Yablonovitch, O. Miller, and S. Kurtz, "Strong Internal and External Luminescence as Solar Cells Approach the Shockley–Queisser Limit," IEEE Journal of Photovoltaics, vol. 2, no. 3, pp. 303-311, July 2012.
- ↑ "Recent facts about photovoltaics in Germany" (PDF). Fraunhofer ISE. 7 January 2015. Retrieved 17 February 2015.
- ↑ Kamran M., Fazal M.R., Mudassar M., Ahmed S.R., Adnan M., Abid I., Randhawa F.J.S., Shams H. Solar photovoltaic grid parity: a review of issues and challenges and status of different PV markets. Int. J. Renew. Energy Resour. 2019;9:244–260.
- ↑ It is important to note that "grid parity" in this context refers to the cost of producing electricity, but not to the total cost of providing electrical energy upon demand. Electric power generation from renewable sources such as solar or wind follows diurnal and seasonal cycles, and is also intermittent. The transition to renewably sourced grid power requires energy storage solutions that help match generation with demand.
- ↑ Staebler, D. L. and Wronski, C. R. Optically induced conductivity changes in discharge-produced hydrogenated amorphous silicon. J. Appl. Physics. 51(6), June 1980.
- ↑ Mishima, T., Taguchi, M., Sakata, H., Maruyama, E., 2011. Development status of high efficiency HIT solar cells. Sol. Energy Mater. Sol. Cell. 95, 18–21. doi:10.1016/j.solmat.2010.04.030