Inorganic Chemistry/Chemical Bonding/Orbital hybridization
In chemistry, hybridisation (or hybridization) is the concept of mixing atomic orbitals into new hybrid orbitals suitable for the pairing of electrons to form chemical bonds in valence bond theory. Hybrid orbitals are very useful in the explanation of molecular geometry and atomic bonding properties.[1]
History and uses
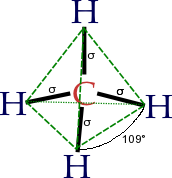
[edit | edit source]Chemist Linus Pauling first developed hybridisation theory[2] in order to explain the structure of molecules such as methane (CH4). Pauling pointed out that a carbon atom forms four bonds by using one s and three p orbitals, so that "it might be inferred" that a carbon atom would form three bonds at right angles (using p orbitals) and a fourth weaker bond using the s orbital in some arbitrary direction. In reality however, methane has four bonds of equivalent strength separated by the tetrahedral bond angle of 109.5°. Pauling explained this by supposing that in the presence of four hydrogen atoms, the s and p orbitals form four equivalent combinations or hybrid orbitals, each denoted by sp3 to indicate its composition, which are directed along the four C-H bonds.[3] Historically, this concept was developed for such simple chemical systems but the approach was later applied more widely, and today it is considered an effective heuristic for rationalizing the structures of organic compounds. It gives a simple orbital picture equivalent to Lewis structures. Hybridisation theory finds its use mainly in organic chemistry.
Hybridisation theory is an integral part of organic chemistry. For drawing reaction mechanisms sometimes a classical bonding picture is needed with two atoms sharing two electrons.[4] Hybridisation theory explains bonding in alkenes[5] and methane.[6] The amount of p character or s character, which is decided mainly by orbital hybridisation, can be used to reliably predict molecular properties such as acidity or basicity.[7]
Overview
[edit | edit source]Orbitals are a model representation of the behavior of electrons within molecules. In the case of simple hybridisation, this approximation is based on atomic orbitals, similar to those obtained for the hydrogen atom, the only atom for which an exact analytic solution to its Schrödinger equation is known. In heavier atoms, like carbon, nitrogen, and oxygen, the atomic orbitals used are the 2s and 2p orbitals, similar to excited state orbitals for hydrogen.
Hybrid orbitals are assumed to be mixtures of atomic orbitals, superimposed on each other in various proportions. For example, in methane, the C hybrid orbital which forms each C-H bond consists of 25% s character and 75% p character and is thus described as sp3 (read as s-p-three) hybridised. Quantum mechanics describes this hybrid as an sp3 wavefunction of the form N[s + (√3)pσ], where N is a normalization constant (here 1/2) and pσ is a p orbital directed along the C-H axis to form a sigma bond. The p-to-s ratio (denoted λ in general) is √3 in this example, and N2λ2 = 3/4 is the p character or the weight of the p component.
In general, any two hybrid orbitals on the same atom must be mutually orthogonal. For an atom with s and p orbitals forming hybrids hi and hj with included angle , the orthogonality condition implies the relation: 1 + ij cos() = 0. The p-to-s ratio for hybrid i is i2, and for hybrid j it is j2. The bond directed towards a more electronegative substituent tends to have higher p-character as stated in Bent's rule. In the special case of equivalent hybrids on the same atom, again with included angle , the equation reduces to just 1 + 2 cos() = 0. For example, BH3 has a trigonal planar geometry, three 120° bond angles, three equivalent hybrids about the boron atom, and thus 1 + 2 cos() = 0 becomes 1 + 2 cos(120°) = 0, giving 2 = 2 for the p-to-s ratio. In other words, sp2 hybrids.
Types of hybridisation
[edit | edit source]sp3
[edit | edit source]For a tetrahedrally coordinated carbon (e.g., methane CH4), the carbon should have 4 orbitals with the correct symmetry to bond to the 4 hydrogen atoms.
Carbon's ground state configuration is 1s2 2s2 2p2 or more easily read:
| C | ↑↓ | ↑↓ | ↑ | ↑ | |
| 1s | 2s | 2p | 2p | 2p |
(Note: The 1s orbital is lower in energy than the 2s orbital, and the 2s orbital is lower in energy than the 2p orbitals)
The carbon atom can utilize its two singly occupied p-type orbitals, to form two covalent bonds with two hydrogen atoms, yielding the singlet methylene CH2, the simplest of the carbenes. The carbon atom can also bond to four hydrogen atoms by an excitation of an electron from the doubly occupied 2s orbital to the empty 2p orbital, so that there are four singly occupied orbitals.
| C* | ↑↓ | ↑ | ↑ | ↑ | ↑ |
| 1s | 2s | 2p | 2p | 2p |
The energy released by formation of two additional bonds more than compensates for the excitation energy required, energetically favouring the formation of four C-H bonds.
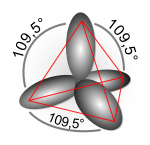
Quantum mechanically, the lowest energy is obtained if the four bonds are equivalent, which requires that they be formed from equivalent orbitals on the carbon. A set of four equivalent orbitals can be obtained that are linear combinations of the valence-shell (core orbitals are almost never involved in bonding) s and p wave functions,[8] which are the four sp3 hybrids.
| C* | ↑↓ | ↑ | ↑ | ↑ | ↑ |
| 1s | sp3 | sp3 | sp3 | sp3 |
In CH4, four sp3 hybrid orbitals are overlapped by hydrogen's 1s orbital, yielding four σ (sigma) bonds (that is, four single covalent bonds) of the same length and strength.
sp2
[edit | edit source]Other carbon based compounds and other molecules may be explained in a similar way as methane. For example, ethene (C2H4) has a double bond between the carbons. The Lewis structure looks like this:

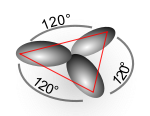
For this molecule, carbon sp2 hybridises, because one π (pi) bond is required for the double bond between the carbons and only three σ bonds are formed per carbon atom. In sp2 hybridisation the 2s orbital is mixed with only two of the three available 2p orbitals:
| C* | ↑↓ | ↑ | ↑ | ↑ | ↑ |
| 1s | sp2 | sp2 | sp2 | 2p |
forming a total of three sp2 orbitals and one remaining p orbital. In ethylene the two carbon atoms form a σ bond by overlapping two sp2 orbitals and each carbon atom forms two covalent bonds with hydrogen by s–sp2 overlap all with 120° angles. The π bond between the carbon atoms perpendicular to the molecular plane is formed by 2p–2p overlap. The hydrogen-carbon bonds are all of equal strength and length, which agrees with experimental data.
sp
[edit | edit source]The chemical bonding in compounds such as alkynes with triple bonds is explained by sp hybridization. In this model, the 2s orbital mixes with only one of the three p-orbitals,
| C* | ↑↓ | ↑ | ↑ | ↑ | ↑ |
| 1s | sp | sp | 2p | 2p |
resulting in two sp orbitals and two remaining p orbitals. The chemical bonding in acetylene (C2H2) consists of sp–sp overlap between the two carbon atoms forming a σ bond and two additional π bonds formed by p–p overlap. Each carbon also bonds to hydrogen in a sigma s–sp overlap at 180° angles.
Hybridisation and molecule shape
[edit | edit source]Hybridisation helps to explain molecule shape, since the angles between bonds are (approximately) equal to the angles between hybrid orbitals.

spx hybridisation
[edit | edit source]As the valence orbitals of main group elements are the one s and three p orbitals with the corresponding octet rule, spx hybridisation is used to model the shape of these molecules.
| Coordination number | Shape | Hybridisation | Examples |
|---|---|---|---|
| 2 | Linear | sp hybridisation (180°) | CO2 |
| 3 | Trigonal planar | sp2 hybridisation (120°) | BCl3 |
| 4 | Tetrahedral | sp3 hybridisation (109.5°) | CCl4 |
| Interorbital angles[9] | |||
spxdy hybridisation
[edit | edit source]As the valence orbitals of transition metals are the five d, one s and three p orbitals with the corresponding 18-electron rule, spxdy hybridisation is used to model the shape of these molecules. These molecules tend to have multiple shapes corresponding to the same hybridisation due to the different d-orbitals involved. As the p-orbitals are not necessarily fully occupied, the square planar shape has 16 valence electrons.[10]
| Coordination number | Shape | Hybridisation | Examples |
|---|---|---|---|
| 4 | Square planar | sp2d hybridisation | PtCl42− |
| 5 | Trigonal bipyramidal | sp3d hybridisation | Fe(CO)5 |
| Square pyramidal | MnCl52− | ||
| 6 | Octahedral | sp3d2 hybridisation | Mo(CO)6 |
| 7 | Pentagonal bipyramidal | sp3d3 hybridisation | ZrF73− |
| Capped octahedral | MoF7− | ||
| Capped trigonal prismatic | TaF72− | ||
| 8 | Square antiprismatic | sp3d4 hybridisation | ReF8− |
| Dodecahedral | Mo(CN)84− | ||
| Bicapped trigonal prismatic | ZrF84− | ||
| 9 | Tricapped trigonal prismatic | sp3d5 hybridisation | ReH92− |
| Capped square antiprismatic |
sdx hybridisation
[edit | edit source]In certain transition metal complexes with a low d electron count, the p-orbitals are unoccupied and sdx hybridisation is used to model the shape of these molecules.[9][11][10]
| Coordination number | Shape | Hybridisation | Examples |
|---|---|---|---|
| 3 | Trigonal pyramidal | sd2 hybridisation (90°) | CrO3 |
| 4 | Tetrahedral | sd3 hybridisation (70.5°, 109.5°) | TiCl4 |
| 5 | Square pyramidal | sd4 hybridisation (65.9°, 114.1°) | Ta(CH3)5 |
| 6 | C3v Trigonal prismatic | sd5 hybridisation (63.4°, 116.6°) | W(CH3)6 |
| Interorbital angles[9] | |||
Hybridisation of hypervalent molecules
[edit | edit source]Octet expansion
[edit | edit source]In some general chemistry textbooks, hybridisation is presented for main group AX5 and above using an "expanded octet" scheme with d-orbitals first proposed by Pauling. However, such a scheme is now considered to be incorrect in light of computational chemistry calculations.
| Coordination number | Shape | Hybridisation | Examples |
|---|---|---|---|
| 5 | Trigonal bipyramidal | sp3d hybridisation | PF5 |
| 6 | Octahedral | sp3d2 hybridisation | SF6 |
| 7 | Pentagonal bipyramidal | sp3d3 hybridisation | IF7 |
In 1990, Magnusson published a seminal work definitively excluding the role of d-orbital hybridization in bonding in hypervalent compounds of second-row elements. This had long been a point of contention and confusion in describing these molecules using molecular orbital theory. Part of the confusion here originates from the fact that one must include d-functions in the basis sets used to describe these compounds (or else unreasonably high energies and distorted geometries result), and the contribution of the d-function to the molecular wavefunction is large. These facts were historically interpreted to mean that d-orbitals must be involved in bonding. However, Magnusson concludes in his work that d-orbital involvement is not implicated in hypervalency.[12][13]
Resonance
[edit | edit source]In light of computational chemistry, a better treatment would be to invoke sigma bond resonance in addition to hybridisation, which implies that each resonance structure has its own hybridisation scheme. All resonance structures must obey the octet rule.[14]
| Coordination number | Resonance structures |
|---|---|
| 5 | Trigonal bipyramidal |

| |
| 6 | Octahedral |

| |
| 7 | Pentagonal bipyramidal |
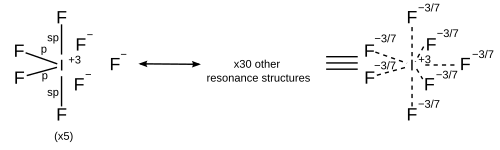
|
Hybridisation in computational VB theory
[edit | edit source]While the simple model of orbital hybridisation is commonly used to explain molecular shape, hybridisation is used differently when computed in modern valence bond programs. Specifically, hybridisation is not determined a priori but is instead variationally optimized to find the lowest energy solution and then reported. This means that all artificial constraints, specifically two constraints, on orbital hybridisation are lifted:
- that hybridisation is restricted to integer values (isovalent hybridisation)
- that hybrid orbitals are orthogonal to one another (hybridisation defects)
This means that in practice, hybrid orbitals do not conform to the simple ideas commonly taught and thus in scientific computational papers are simply referred to as spx, spxdy or sdx hybrids to express their nature instead of more specific integer values.
Isovalent hybridisation
[edit | edit source]Although ideal hybrid orbitals can be useful, in reality most bonds require orbitals of intermediate character, analogous to intermediate ionic-covalent character. This requires an extension to include flexible weightings of atomic orbitals of each type (s, p, d) and allows for a quantitative depiction of bond formation when the molecular geometry deviates from ideal bond angles. The amount of p-character is not restricted to integer values; i.e., hybridisations like sp2.5 are also readily described.
The hybridisation of bond orbitals is determined by Bent's rule: "Atomic s character concentrates in orbitals directed toward electropositive substituents".
For molecules with lone pairs, the bonding orbitals are isovalent spx hybrids. For example, the two bond-forming hybrid orbitals of oxygen in water can be described as sp4.0 to give the interorbital angle of 104.5°.[15] This means that they have 20% s character and 80% p character and does not imply that a hybrid orbital is formed from one s and four p orbitals on oxygen since the 2p subshell of oxygen only contains three p orbitals.
Hybridization defects
[edit | edit source]Hybridisation of s and p orbitals to form effective spx hybrids requires that they have comparable radial extent. While 2p orbitals are on average less than 10% larger than 2s, in part attributable to the lack of a radial node in 2p orbitals, 3p orbitals which have one radial node, exceed the 3s orbitals by 20–33%.[16] The difference in extent of s and p orbitals increases further down a group. The hybridisation of atoms in chemical bonds can be analysed by considering localised molecular orbitals, for example using natural localised molecular orbitals in a natural bond orbital (NBO) scheme. In methane, CH4, the calculated p/s ratio is approximately 3 consistent with "ideal" sp3 hybridisation, whereas for silane, SiH4, the p/s ratio is closer to 2. A similar trend is seen for the other 2p elements. Substitution of fluorine for hydrogen further decreases the p/s ratio.[17] The 2p elements exhibit near ideal hybridisation with orthogonal hybrid orbitals. For heavier p block elements this assumption of orthogonality cannot be justified. These deviations from the ideal hybridisation were termed hybridisation defects by Kutzelnigg.[18]
However, computational VB groups such as Gerratt, Cooper and Raimondi (SCVB) as well as Shaik and Hiberty (VBSCF) go a step further to argue that even for model molecules such as methane, ethylene and acetylene, the hybrid orbitals are already defective and nonorthogonal, with hybridisations such as sp1.76 instead of sp3 for methane.[19]
Photoelectron spectra
[edit | edit source]One misconception concerning orbital hybridisation is that it incorrectly predicts the ultraviolet photoelectron spectra of many molecules. While this is true if Koopmans' theorem is applied to localized hybrids, quantum mechanics requires that the (in this case ionized) wavefunction obey the symmetry of the molecule which implies resonance in valence bond theory. For example, in methane, the ionized states (CH4+) can be constructed out of four resonance structures attributing the ejected electron to each of the four sp3 orbitals. A linear combination of these four structures, conserving the number of structures, leads to a triply degenerate T2 state and a A1 state.[20] The difference in energy between the ionized state and the ground state would be the ionization energy, which yields two values in agreement with experiment.

Localized MOs vs canonical MOs
[edit | edit source]Bonding orbitals formed from hybrid atomic orbitals may be considered as localized molecular orbitals, which can be formed from the delocalised orbitals of molecular orbital theory by an appropriate mathematical transformation. For molecules in the ground state, this transformation of the orbitals leaves the total many-electron wave function unchanged. The hybrid orbital description of the ground state is therefore equivalent to the delocalised orbital description for ground state total energy and electron density, as well as the molecular geometry that corresponds to the minimum total energy value.
Two localized representations
[edit | edit source]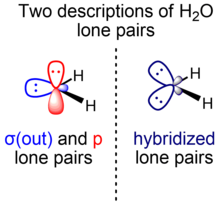
Molecules with multiple bonds or multiple lone pairs can have orbitals represented in terms of sigma and pi symmetry or equivalent orbitals. Different valence bond methods use either of the two representations, which have mathematically equivalent total many-electron wave functions and are related by a unitary transformation of the set of occupied molecular orbitals.
For multiple bonds, the sigma-pi representation is the predominant one compared to the equivalent orbital (bent bond) representation. In contrast, for multiple lone pairs, most textbooks use the equivalent orbital representation. However, the sigma-pi representation is also used, such as by Weinhold and Landis within the context of natural bond orbitals, a localized orbital theory containing modernized analogs of classical (valence bond/Lewis structure) bonding pairs and lone pairs.[21] For the hydrogen fluoride molecule, for example, two F lone pairs are essentially unhybridized p orbitals, while the other is an spx hydrid orbital. An analogous consideration applies to water (one O lone pair is in a pure p orbital, another is in an spx hybrid orbital).
References
[edit | edit source]- ↑ "It is important to recognize that the VSEPR model provides an approach to bonding and geometry based on the Pauli principle that is completely independent of the valence bond (VB) theory or of any orbital description of bonding." Gillespie, R. J. J. Chem. Educ. 2004, 81, 298–304.
- ↑ L. Pauling, J. Am. Chem. Soc. 53 (1931), 1367
- ↑ L. Pauling The Nature of the Chemical Bond (3rd ed., Oxford University Press 1960) p.111–120.
- ↑ Organic Chemistry. Jonathan Clayden, Nick Greeves, Stuart Warren, and Peter Wothers 2001 ISBN 0-19-850346-6
- ↑ Organic Chemistry, Third Edition Marye Anne Fox James K. Whitesell 2003 ISBN 978-0-7637-3586-9
- ↑ Organic Chemistry 3rd Ed. 2001 Paula Yurkanis Bruice ISBN 978-0-130-17858-9
- ↑ "Acids and Bases". Orgo Made Simple. Retrieved 23 June 2015.
- ↑ McMurray, J. (1995). Chemistry Annotated Instructors Edition (4th ed.). Prentice Hall. p. 272. ISBN 0-13-140221-8
- ↑ a b c Weinhold, Frank; Landis, Clark R. (2005). Valency and bonding: A Natural Bond Orbital Donor-Acceptor Perspective. Cambridge: Cambridge University Press. pp. 367, 374–376, 381–383. ISBN 978-0-521-83128-4.
- ↑ a b Bayse, Craig; Hall, Michael (1999). "Prediction of the Geometries of Simple Transition Metal Polyhydride Complexes by Symmetry Analysis". J. Am. Chem. Soc. 121 (6): 1348–1358. doi:10.1021/ja981965+.
- ↑ Kaupp, Martin (2001). ""Non-VSEPR" Structures and Bonding in d(0) Systems". Angew Chem Int Ed Engl. 40 (1): 3534–3565. doi:10.1002/1521-3773(20011001)40:19<3534::AID-ANIE3534>3.0.CO;2-#.
- ↑ E. Magnusson. Hypercoordinate molecules of second-row elements: d functions or d orbitals? J. Am. Chem. Soc. 1990, 112, 7940–7951. doi:10.1021/ja00178a014
- ↑ David L. Cooper , Terry P. Cunningham , Joseph Gerratt , Peter B. Karadakov , Mario Raimondi (1994). "Chemical Bonding to Hypercoordinate Second-Row Atoms: d Orbital Participation versus Democracy". Journal of the American Chemical Society. 116 (10): 4414–4426. doi:10.1021/ja00089a033.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Richard D. Harcourt; Thomas M. Klapötke (2003). "Increased valence (qualitative valence bond) descriptions of the electronic structures of electron-rich fluorine-containing molecules". Journal of Fluorine Chemistry. 123 (1): 5–20. doi:10.1016/S0022-1139(03)00012-5.
- ↑ Frenking, Gernot; Shaik, Sason, eds. (2014). "Chapter 3: The NBO View of Chemical Bonding". The Chemical Bond: Fundamental Aspects of Chemical Bonding. John Wiley & Sons. ISBN 9783527664719.
- ↑ Kaupp, Martin (2007). "The role of radial nodes of atomic orbitals for chemical bonding and the periodic table". Journal of Computational Chemistry. 28 (1): 320–325. doi:10.1002/jcc.20522. ISSN 0192-8651.
- ↑ Kaupp, Martin (2014) [1st. Pub. 2014]. "Chapter 1: Chemical bonding of main group elements". In Frenking, Gernod; Shaik, Sason (eds.). The Chemical Bond: Chemical Bonding Across the Periodic Table. Wiley-VCH. ISBN 978-1-234-56789-7.
{{cite book}}: Unknown parameter|lastauthoramp=ignored (|name-list-style=suggested) (help) - ↑ Kutzelnigg, W. (August 1988). "Orthogonal and non-orthogonal hybrids". Journal of Molecular Structure: THEOCHEM. 169: 403–419. doi:10.1016/0166-1280(88)80273-2.
- ↑ Shaik, Sason; Danovich, David; Hiberty, Philippe (2022). "On the nature of the chemical bond in valence bond theory". The Journal of Chemical Physics. 157: 090901. doi:10.1063/5.0095953.
- ↑ Sason S. Shaik; Phillipe C. Hiberty (2008). A Chemist's Guide to Valence Bond Theory. New Jersey: Wiley-Interscience. ISBN 978-0-470-03735-5.
- ↑ Weinhold, Frank; Landis, Clark R. (2012). Discovering Chemistry with Natural Bond Orbitals. Hoboken, N.J.: Wiley. pp. 67–68. ISBN 978-1-118-11996-9.