Inorganic Chemistry/Chemical Bonding/MO Diagram
A molecular orbital diagram or MO diagram for short is a qualitative descriptive tool explaining chemical bonding in molecules in terms of molecular orbital theory in general and the linear combination of atomic orbitals molecular orbital method (LCAO method) in particular.[1][2][3] This tool is very well suited for simple diatomic molecules such as dihydrogen, dioxygen and carbon monoxide but becomes more complex when discussing polynuclear molecules such as methane. It explains why some molecules exist and not others, how strong bonds are, and what electronic transitions take place.
Dihydrogen MO diagram
[edit | edit source]The smallest molecule, hydrogen gas exists as dihydrogen (H-H) with a single covalent bond between two hydrogen atoms. As each hydrogen atom has a single 1s atomic orbital for its electron, the bond forms by overlap of these two atomic orbitals. In figure 1 the two atomic orbitals are depicted on the left and on the right. The vertical axis always represents the orbital energies. The atomic orbital energy correlates with electronegativity as a more electronegative atom holds an electron more tightly thus lowering its energy. MO treatment is only valid when the atomic orbitals have comparable energy; when they differ greatly the mode of bonding becomes ionic. Each orbital is singly occupied with the up and down arrows representing an electron.
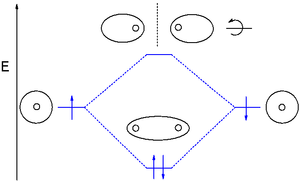
The two AO's can overlap in two ways depending on their phase relationship. The phase of an orbital is a direct consequence of the oscillating, wave-like properties of electrons. In graphical representations, the orbital phase is depicted either by a plus or minus sign (confusing because there is no relationship to electrical charge) or simply by shading. The sign of the phase itself does not have physical meaning except when mixing orbitals to form molecular orbitals.
Then two same-sign orbitals have a constructive overlap forming a molecular orbital with the bulk of electron density located between the two nuclei. This MO is called the bonding orbital and its energy is lower than that of the original atomic orbitals. The orbital is symmetrical with respect to rotation around the molecular axis (no change) and therefore also called a sigma bond (σ-bond).
The two hydrogen atoms can also interact with each other with their 1s orbitals out-of-phase which leads to destructive cancellation and no electron density between the two nuclei depicted by the so-called nodal plane as the vertical dashed line. In this anti-bonding MO with energy much higher than the original AO's the electrons are located in lobes pointing away from the central axis. Like the bonding orbital this orbital is symmetrical but differentiated from it by an asterisk σ* bond
The next step in constructing an MO diagram is filling the molecular orbitals with electrons. With the case of dihydrogen at hand two electrons have to be distributed over a bonding orbital and an anti-bonding orbital. Three general rules apply:
- The Aufbau principle states that orbitals are filled starting with the lowest energy
- The Pauli exclusion principle states that the maximum number of electrons occupying an orbital is two having opposite spins
- Hund's rule states that when there are several MO's with equal energy the electrons fill one MO at a time.
Application of these rules for dihydrogen results in having both electrons in the bonding MO. This MO is called the Highest Occupied Molecular Orbital or HOMO which makes the other orbital the Lowest Unoccupied Molecular Orbital or LUMO. The electrons in the bond MO are called bonding electrons and any electrons in the antibonding orbital would be called antibonding electrons. The reduction in energy of these electrons is the driving force for chemical bond formation. For bonding to exist the bond order defined as:
must have a value larger than 0. The bond order for dihydrogen is (2-0)/2 = 1.
This MO diagram also helps explain how a bond breaks. When applying energy to dihydrogen, a molecular electronic transition takes place when one electron in the bonding MO is promoted to the antibonding MO. The result is that there is no longer a net gain in energy.
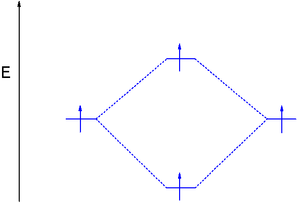
Dihelium MO diagram
[edit | edit source]Dihelium' (He-He) is a hypothetical molecule and MO theory helps to explain why. The MO diagram for dihelium (2 electrons in each 1s AO) looks very similar to that of dihydrogen but instead of 2 electrons it is now required to place 4 electrons in the newly formed molecular orbitals.

The only way to accomplish this is by occupying the antibonding orbital with two electrons as well which reduces the bond order ((2-2)/2) to zero and cancels the net energy stabilization.
Another molecule that is precluded based on this principle is diberyllium (beryllium with electron configuration 1s22s2). On the other hand, by removing one electron from dihelium, the stable gas-phase species He2+ ion is formed with bond order 1/2.
Dilithium MO diagram
[edit | edit source]Next up in the periodic table is lithium and MO theory correctly predicts that dilithium is a stable molecule with bond order 1. The 1s MO's are completely filled and do not participate in bonding.

Dilithium is a gas-phase molecule with a much lower bond strength than dihydrogen because the 2s electrons are further removed from the nucleus.
Diboron MO diagram
[edit | edit source]The MO diagram for diboron (B-B electron configuration boron: 1s22s22p1) requires the introduction of an atomic orbital overlap model for p orbitals. The three dumbbell-shaped p-orbitals have equal energy and are oriented mutually perpendicular (or orthogonal). The p-orbitals oriented in the x-direction (px) can overlap end-on forming a bonding (symmetrical) σ orbital and an antibonding σ* molecular orbital. In contrast to the σ1s MOs, the σ2p has some electron density at either side of the nuclei that has a phase (blue) opposite that of the electron density between the nuclei (white). The σ*2p also has some electron density between the nuclei. (Note that in this figure, the phases [colors] of the σ*2p orbital are slightly incorrect: the phases of the right-hand lobes of electron density should be switched so that the colors go blue, white, blue, white.)

The other two p-orbitals py and pz can overlap side-on. The resulting bonding orbital has its electron density in the shape of two sausages above and below the plane of the molecule. The orbital is not symmetrical around the molecular axis and is therefore a pi orbital. The antibonding pi orbital (also asymmetrical) has four lobes pointing away from the nuclei. Both py and pz orbitals form a pair of pi orbitals equal in energy (degenerate) and can be higher or lower than that of the sigma orbital.
In diboron the 1s and 2s electrons do not participate in bonding but the single electrons in the 2p orbitals occupy the 2πpy and the 2πpz MO's resulting in bond order 1. Because the electrons have equal energy (they are degenerate) diboron is a diradical and since the spins are parallel the compound is paramagnetic.

Like diboron, dicarbon (C-C electron configuration:1s22s22p2) is a reactive gas-phase molecule. Two additional electrons are placed in the 2πp MO's increasing the bond order to 2. The bond order for dinitrogen is three because now two electrons are added in the 2σ MO as well.
Dioxygen MO diagram
[edit | edit source]MO treatment of dioxygen is different from that of the previous diatomic molecules because the pσ MO is now lower in energy than the 2π orbitals. This is attributed to interaction between the 2s MO and the 2pz MO.[4] Distributing 8 electrons over 6 molecular orbitals leaves the final two electrons as a degenerate pair in the 2pπ* antibonding orbitals resulting in a bond order of two. Just as diboron, this type of dioxygen called triplet oxygen is a paramagnetic diradical. When both HOMO electrons pair up the other oxygen type is called singlet oxygen.

The bond order decreases and the bond length increases in the order O2+ (112.2 pm), O2 (121 pm), O2- (128 pm) and O22- (149 pm).[4]
In difluorine two additional electrons occupy the 2pπ* with a bond order of 1. In dineon Ne2 (as with dihelium) the number of bonding electrons equals the number of antibonding electrons and this compound does not exist.
References
[edit | edit source]- ↑ Organic Chemistry. Jonathan Clayden, Nick Greeves, Stuart Warren, and Peter Wothers 2001 ISBN 0-19-850346-6
- ↑ Organic Chemistry, Third Edition Marye Anne Fox James K. Whitesell 2003 ISBN 978-0-7637-3586-9
- ↑ Organic Chemistry 3rd Ed. 2001 Paula Yurkanis Bruice ISBN 0-13-017858-6
- ↑ a b Modern Inorganic Chemistry William L. Jolly 1985 ISBN 0-07-032760-2

