IB Physics/Thermal Physics
3.1 Thermal concepts
[edit | edit source]3.1.1 State that temperature determines the direction of thermal energy transfer between two objects.
[edit | edit source]Thermal energy is transferred down, from a high temperature to a low temperature.
3.1.2 State the relation between the Kelvin and Celsius scales of temperature
[edit | edit source]T(K) = t/(°C) +273
To convert temperature in degree Celsius to temperature in Kelvin add 273.15. To convert temperature in Kelvin to temperature in degree Celsius subtract 273.15.
3.1.3 State that the internal energy of a substance is the total potential energy and random kinetic energy of the molecules of the substance
[edit | edit source]
3.1.4 Explain and distinguish between the macroscopic concepts of temperature, internal energy and thermal energy (heat)
[edit | edit source]| Concept | Explanation |
|---|---|
| Temperature | Is a measure of the average kinetic energy of the molecules in a substance |
| Internal Energy | Is the measure of the average kinetic and potential energy in a substance |
| Thermal Energy | Is the non-mechanical transfer of energy between a system and its surroundings |
3.1.5 and 3.1.6 Define the mole and molar mass. Define the Avogadro constant.
[edit | edit source]| Word | Definition |
|---|---|
| Mole | The amount of substance that contains the same number of particles as there are atoms in 12g of carbon-12 |
| Molar Mass | The mass of one mole of a substance |
| Avogadro's constant | Is the number of particles in a mole. This number can be found in the IB Physics data booklet to be equal to 6.023 × 1023 |
3.2 Thermal properties of matter
[edit | edit source]Specific heat capacity, phase changes and latent heat
[edit | edit source]3.2.1 Define specific heat capacity and thermal capacity
[edit | edit source]| Word | Definition |
|---|---|
| Specific Heat Capacity (SHC) | The amount of thermal energy required for 1kg of a substance to raise its temperature by 1K |
| Thermal Capacity | The amount of thermal energy required for a substance to raise its temperature by 1K |
3.2.2 Solve problems involving specific heat capacities and thermal capacities.
[edit | edit source]3.2.3 Explain the physical differences between the solid, liquid and gaseous phases in terms of molecular structure and particle motion
[edit | edit source]| Phase | Explanation |
|---|---|
| Solid | Macroscopically, are in fixed volumes and a fixed shape. Molecules vibrate about an average position. |
| Liquid | Are in a fixed volume but its shape can change. The molecules are vibrating but not fixed to a position. The molecules are free to move. |
| Gas | Molecules will expand to fill the container. The molecules are not in a fixed position. |
3.2.4 Describe and explain the process of phase changes in terms of molecular behaviour
[edit | edit source]| Phase Change | Explanation |
|---|---|
| Freezing | Slower moving liquid molecules begin to lose energy to become fixed to a position. Liquid to solid change. |
| Melting | Fixed solid molecules gain energy and begin to move more. Solid to liquid change. |
| Evaporation | Faster moving molecules in a liquid's surface escapes, cooling the liquid. Liquid to gas change. |
| Boiling | Faster moving molecules throughout the liquid escapes. Liquid to gas change. |
| Condensation | Slower gas molecules lose energy. Gas to liquid change. |
3.2.5 Explain in terms of molecular behaviour why temperature does not change during a phase change.
[edit | edit source]A phase change is associated with an increase or decrease in the potential energy of a molecule, not the kinetic energy. Hence, there is no temperature change during a phase change.
3.2.6 Distinguish between evaporation and boiling
[edit | edit source]Evaporation takes place at the surface of the liquid, whilst boiling takes place throughout the liquid.
3.2.7 Define specific latent heat
[edit | edit source]Specific latent heat is the amount of energy per unit mass absorbed or released during a change of phase.
Whereby,
L= Specific latent heat in Jkg^-1
Q= Energy in J
m= mass in kg
3.2.8 Solve problems involving specific latent heats
[edit | edit source]Kinetic model of an ideal gas
[edit | edit source]3.2.9 Define pressure
[edit | edit source]Pressure is the force exerted per unit area. It is measured in pascals.
3.2.10 State the assumptions of the kinetic model of an ideal gas.
[edit | edit source]Assumptions:
- Newton's laws apply to molecular behavior
- No intermolecular forces exist
- The molecules are points
- The collisions are elastic
- No time was spent on these collisions
3.2.11 State that temperature is a measure of the average random kinetic energy of the molecules of an ideal gas.
[edit | edit source]Temperature is a measure of the average random kinetic energy of the molecules of an ideal gas
3.2.12 Explain the macroscopic behaviour of an ideal gas in terms of a molecular model.
[edit | edit source]| Law | Effect on the ideal gas |
|---|---|
| Pressure Law | Pressure of a gas is proportional to its temperature |
| Charles' Law | The volume of gas is proportional to its temperature |
| Boyle's Law | The pressure of a gas is inversely proportional to its volume |
Old Syllabus
[edit | edit source]Maxwell-Boltzmann Distribution Curve
The speed (or energy) distribution curve for a gas usually has speed on the x-axis, and number of molecules on y. The curve goes from the origin up to a peak, and then down exponentially as if the x-axis were an asymptote. Higher temperatures are 'flatter' with a lower peak, but a slower decrease beyond it.
10.2 Evaporation and thermal expansion
[edit | edit source]10.2.1
[edit | edit source]Evaporation is the process by which individual molecules escape from a liquid. This occurs with any liquid, and, unless the liquid is in an enclosed system, eventually all the liquid will evaporate.
As the liquid evaporates, it's temperature is reduced. The cooling effect results from the fact that it is the fast moving molecules which escape, leaving behind the slow ones. This means that the average speed of the molecules is reduced, and thus the temperature of the liquid is reduced. This is the principle behind evaporative cooling.
10.2.2
[edit | edit source]The coefficient of linear expansion has the symbol a, and defines how much the length of an object (say a wire) changes for a give change in temperature. It is used in the equation ΔL = a x L0 x ΔT, where L0 is the initial length, and ΔL is the change.
It is (apparently) important to understand that L0 should appear in this equation. The expansion is a result of molecules moving faster, and thus further apart as they vibrate. As a result, the more molecules there are, the greater the expansion of a given change in them will be, because the space between all the molecules expands.
10.2.3
[edit | edit source]Thermal expansion of a solid results from increased amplitude of vibrations of the component particles. As the temperature is increased (i.e. heat is added) the particles gain more energy, which becomes Ek (though not translational), resulting in bigger vibrations. Due to this, there is greater space between the molecules, and so the overall solid becomes larger.
10.2.4
[edit | edit source]The linear expansion equation can be applied in any direction (in most substances), and so it is possible to use it to find expansion in both area and volume. To find the area, just find the expansion in two perpendicular directions, then find the change in area as a result of the two changes. For volume, find the expansion in three perpendicular directions, and find the change in volume.
10.2.5
[edit | edit source]Making use of thermal expansion
- Bimetallic strips (where two different strips, with different values of a are bonded in the middle), when heated or cooled, bend over (because the metal on one side is expanding/contracting faster than the other). This can be used to complete or break circuits, and is often used in thermostats (i.e. things which turn a heater on if the temperature falls below, or off it is above a certain temperature).
- When a ring of metal expands, both the outside edge and the hole in the middle expand (which might not be obvious, but is true). Thus, the 'hole' can be expanded to make a ring fit over something, which then locks tight when it cools. This technique is used in fitting bands around wagon wheels (which is done really often these days).
- Volume expansion of liquids is the basis for both mercury and alcohol thermometers. As the temperature increases, the volume of the mercury increases, pushing it up the tube.
Overcoming problems with thermal expansion
- Bridges are constructed of concrete blocks which will expand into one another and shatter if the temperature is increased. To combat this, gaps are left between the blocks, for them to expand into. This is why there are gaps in bridges, and results in that 'thunk, thunk' sound as you drive over them. The same goes for railway tracks.
- Steam pipes must be allowed to expand, because they have large variations in temp (i.e., when there is vs isn't steam in them). To allow for this, the pipes are connected to 'corner' junctions. These are sort of an L shape, so the vertical pipe can expand up or down in the junctions, and the horizontal one left and right without distorting the shape of the pipe (it also creates a series of short sections where expansion occurs, rather than one long one, which would be harder to deal with).
10.3 : Thermodynamics
[edit | edit source]10.3.1
[edit | edit source]Thermodynamics is used to describe the relationships between thermodynamic variables in different parts of thermodynamics systems. The primary example of thermodynamic variables are heat, work and entropy but there are many more, such as pressure, volume, surface tension, magnetizability and (molar) concentration. All these changes are studied in the context of the transfer of heat, work and entropy both in and out of systems. Classical thermodynamics is concerned entirely with states of equilibrium, so no quantity with the dimensions of time occur in its equations. Only the direction of time may occur (before, after). 64.134.223.225 (discuss) 02:08, 26 August 2014 (UTC)
10.3.2
[edit | edit source]Heat and work are both forms of energy, and thus, heating an object or performing work on it causes a transfer of energy. A performing work on B, increases B's internal energy, while decreasing A's and so on.
10.3.3
[edit | edit source]A system in thermodynamics is something which has a certain amount of internal energy.
Take a block of metal could, for example. Heat can be put into or taken out of it. The concept of work being done on or by it is a bit fuzzy, but possible to imagine.
A fixed mass of gas could also be a system. Heat can go in or out, and if you compress it, you are doing work (and thus increasing the internal energy), If the gas does work (i.e. is allowed to expand but pushing a piston back or something) then its internal energy decreases.
A thermodynamic process is any process in which heat is taken out of, or put into a system, or where work is done on or by it.
10.3.4
[edit | edit source]If a gas is quickly compressed, then it's temperature is increased. Work has been done by compressing the gas, which has been converted into internal energy. If the gas is then allowed to cool, heat equal to the amount of energy supplied by the work will be released into the surroundings.
The reverse happens if the gas is allowed to expand. Temperature (and internal energy) is decreased, and the system then absorbs heat from the surroundings. To state it another way, work (to expand) is done by the system, resulting in a loss of internal energy, but heat will then be absorbed back in if the system is left do so.
Work is converted to heat (in the first case) and heat is converted to work in the second.
10.3.5
[edit | edit source]Isothermal : Isothermal processes are those in which there is no change in internal energy ( or temperature ). An example of such a process could be expanding or compressing a gas very slowly, so as work is done on or by the system, heat is absorbed from/released to the surroundings. Thus the temperature remains constant, even though work is being done, and heat is being transferred. In an isothermal process, the work done and the heat transferred out must occur in opposing directions at the same rate.
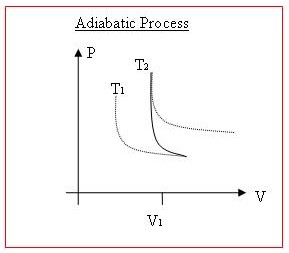
Adiabatic : Adiabatic processes are those in which ΔQ is zero (i.e. no heat leaves or enters the system). The most common example of this is compressing or expanding a gas very quickly, so there is no time for heat to be transferred. In such a process, internal energy (i.e. temp) changes as work is done.
Isochoric : Isochoric processes are those in which ΔV is zero (i.e the change in volume is zero). In such a process, the work done by the system is zero. An example would be to place a closed tin can containing only air into a fire. To a first approximation, the can will not expand, and the only change will be that the gas gains internal energy, as evidenced by its increase in temperature and pressure. Mathematically, ΔQ = ΔU.
Isobaric : Isobaric processes are those in which the pressure remains constant. A simple example would be heating a pot of water with the lid removed, so that the surface of the water would be subjected to a constant pressure (atmospheric).
10.3.6
[edit | edit source]Illustrating these thermodynamic processes on P-V diagrams (pressure vs. volume) is another thing which would be much nicer with diagrams.
When work is done on/by a gas, or when heat is transferred into/out of it, both volume and pressure will normally change. Lines of equal temperature on a P vs. V graph curves, have asymptotes to both the x axis and the y axis. Higher temperature curves are further away from the origin.
An Isothermal process will exactly follow one of these temperature curves, since internal energy is constant.
With an adiabatic process, as work is being done on the system, temperature will increase, and so the point on the graph will move 'up' to a higher temp curve. If work is being done by the system, then the point will move 'down' to a lower temperature curve.
Other than that, the resulting curve on a P vs V graph will usually be determine by the nature of the process. Sometimes only Pressure will change (more gas could be added, or temperature could change) and sometimes only volume will change, (temperature could decrease as the volume is reduced, keeping the pressure constant.).
Also worth noting (though I don't know if it's necessary) is that the area under the curve is equal to work done by the system (which gets confusing in the next section).
10.3.7
[edit | edit source]ΔU = ΔQ + ΔW
This equation relates changes in heat and work to changes in internal energy. The actual signs are a bit of a tricky issue, but can be remembered if we know that a positive ΔU value will result in an increased temperature. Based on this, we then know that temperature will be increased by adding heat to the system, so ΔQ is positive when heat is added to the system.
Similarly, if work is done on the system, temperature will be increased, so ΔW is positive for work done on the system. From this, obviously, ΔQ is negative when heat is released to the surroundings, and ΔW is negative when work is done by the system.
This equation can be applied by substituting in two values, and finding the third. The equation can be simplified in isothermal processes since we know ΔU is zero, and in adiabatic processes since we know ΔQ is zero.
10.3.8
[edit | edit source]A thermodynamic cycle is where a series of thermodynamic processes eventually put the system back into its initial state, from which the process can be repeated. This idea is used by heat engines, which use a repeated series of thermodynamic processes to produce mechanical energy from heat energy. There are two main types of heat engines (internal and external combustion) which are described below.
External combustion engines : These are the old sort of engines which are used in steam trains. Heat is used to boil water, which turns to steam, increasing the pressure in the pipes above. This increased pressure forces a piston down (the piston being connected to whatever is appropriate for what the engine is doing). Once it is forced all the way down, a valve is released, and the steam is allowed to escape into another set of pipes which eventually return it to the boiler (via a condenser). This reduces the pressure, and the piston is pushed back up, either by other pistons in a cam shaft, or by springs. When it reaches the top again, more steam is allowed in, forcing the piston down again. It is also possible to use a turbine where the steam is used to spin a turbine, resulting in rotational motion (this is often used in power generation). I think that's all we really need to know, internal combustion is the more important one here.
Internal combustion engines : These are the type commonly used in cars today, where the petrol is actually ignited in the cylinder. They are known as 4 stroke, because the process occurs in two cycles (two up strokes, and two down strokes). The piston begins at the top of the cylinder, moving down. The intake valve is opened, and so a mixture of fuel and oxygen is sucked into the cylinder. When the piston reaches the bottom, the valve is closed, and the piston moves up, compressing the mixture until the piston reaches the top. When the piston is at the top, the spark plug fires, igniting the mixture, producing high downward pressure on the piston. This pressure pushes the piston down (this is where the actual work is done by the engine). When the piston reaches the bottom, the exhaust valve is opened and as the piston moves up the exhaust is pushed out. After reaching the top, the exhaust valve is closed, and the intake valve opened (bringing us back to the start). All this can be expressed on a P-V diagram (anyone want to draw it?). There will be a diagram in most physics text books in the meantime.
10.3.9
[edit | edit source]Entropy (symbol S) is a measure of the disorder in a system. There's a big complicated explanation relating to probability, meta-states and information theory, but I don't think it's necessary. Basically, entropy always increases. It can be decreased in a system, but it will increase in the surroundings of that system as a result. This is the second law of thermodynamics; natural systems tend to move towards a state of greater disorder. In energy terms, increased disorder is energy being more evenly distributed. If there is a point of high energy, and a point of low energy, it is possible to use this difference to do work, entropy tends to decrease this difference. To put it another way, energy tends to spread out evenly rather than concentrating at one point.
10.3.10
[edit | edit source]Natural systems tend to move towards a state of more disorder (second law of thermodynamics). What this means is that you can't build an engine which will convert 100% of the energy put into it into work (i.e. no engine can be 100% efficient). The first law, for example, suggests that a block of wood sitting on the table could convert some of it's heat energy into work and jump off the table, but the second law says it isn't going to happen (not that it couldn't, just that it's really, really unlikely).
Also, since it doesn't fit in anywhere else, but is in the data book, the equation ΔS = ΔQ/ΔT allows the change in entropy to be found (where Q = heat, and T = temperature). This is actually a calculus equation, but for small changes in T, it's a good enough approximation to use average temperature.
10.3.11
[edit | edit source]Refrigerators : The basic idea is to do work to over come entropy, producing an area of lower temperature inside, and higher outside. This process occurs with a set of pipes running along the outer wall, and the inner wall of the system. Low pressure (and so cold) gas runs through the inner pipes, which absorbs heat from the inside of the refrigerator. This gas is then pressurised using a condenser (a piston) and pumped through the outside pipes. Because this gas has had work done on it, heat escapes from it to the outside of the refrigerator. The gas is then slowly allowed through a valve connected to the low pressure pipes to be recirculated. In this way, heat is transferred from the inside to the outside, even though the temperature inside is already lower. This may seem to violate the second law, but the overall entropy of the universe is actually being increased, because energy is required to make it happen (to drive the condenser). The efficiency of such a system is defined by the equation Efficiency = QH-QL / QL, where efficiency is the efficiency of the refrigerator (1 is perfect, or 100% efficient), QL is the low (inside) temperature, and QH is the high (outside temperature).
Heat Pump : A heat pump is a special form of a heater, usually installed together with air conditioning capabilities in an HVAC system when the expected climatic variations make it more economical than to intall and use a direct heater. Rather than rely on pure generation of heat, a heat pump moves heat (more accurately: thermal energy) from one place to another. A heat pump works by doing work to move heat from the cold outside to the hotter inside. It is just the reverse of the refrigerator described above. The efficiency of such a pump will be Efficiency = QH-QL / QH, working as above.
Note that in each case, this equation is like the one in the data book, but the denominator will have to be chosen based on what the particular process is supposed to achieve.
10.3.12
[edit | edit source]If we feel like getting all philosophical about things, entropy can be thought of as what defines 'forward' and 'backward' for time. As time progresses, entropy increases and so it lets us think about time as going forward when entropy is increasing. As above, heat pumps and refrigerators are capable of lowering entropy in a system, but increase it for the whole system + environment. When ice (or something else) melts it is absorbing heat, and thus entropy is increasing. The movements from solid to liquid to gas also mark an increase in entropy, as particles are moving more and more randomly.