IB Physics/Relativity
H.1 Introduction to relativity
[edit | edit source]H.1.1 Describe what is meant by a frame of reference
[edit | edit source]A frame of reference refers to a point of view. Physics refers to observational frames of reference, i.e. what is heard, seen, touched, smelt or tasted from a certain point of view.
e.g. you have a frame of reference (in a computer chair) that views the world as stationary. A frame of reference with the sun as stationary would view you as moving around the earth.
H.1.2 Describe what is meant by a Galilean Transformation
[edit | edit source]Galilean is what seems intuitive. The equations do not involve relativity.
H.1.3 Solve problems involving relative velocities using the Galilean transformation equations
[edit | edit source]This should be easy. position equation: x'=x-vt
Velocity equation: u'=u-v
e.g. You are sitting on a park bench. You see a bike and car moving away from each other. The bike is moving at 5m/s, the car is moving at 20 m/s. How fast is the bike moving in the cars reference frame? (Ans: 25m/s)
H.2 Concepts and postulates of special relativity
[edit | edit source]H.2.1 Describe what is meant by an inertial frame of reference
[edit | edit source]A reference frame that is moving with a constant velocity. This really isn't that essential but you might see a fundamental flaw in this definition (just ignore it if you do).
H.2.2 State the two postulates of the special theory of relativity
[edit | edit source]- the speed of light in a vacuum is constant for all inertial observers.
- The laws of physics are the same for all inertial observers.
H.2.3 Discuss the concept of simultaneity
[edit | edit source]Consult a textbook (or youtube "simultaneity"), best explained with diagrams.
In summary though, simultaneous events that take place at the same point in space will be simultaneous to all observers. However, events that take place at different points in space can be simultaneous for one observer but not for another.
H.3 Relativistic Kinematics
[edit | edit source]H.3.1 Describe the concept of a light clock
[edit | edit source]Best described by diagram.
Imagine a clock where light is bounced off two mirrors. mirror| light beam --> mirror |
Each time it hits a mirror a "tick" is registered. Since light is the same for all reference frames, this is the most accurate type of clock.
This seams simple for a stationary clock, HOWEVER in a reference frame where the clock moves, it must travel a diagonal distance which is greater than that for a stationary time frame. In this case a "tick" would take longer for one reference frame than the other. Therefore, time is shorter for one reference frame than another.
H.3.2 Define proper time interval
[edit | edit source]Proper time interval is the elapsed time measured between two events when the observer is in an inertial frame of reference.
H.3.3 Derive the time dilation formula
[edit | edit source]The time dilation formula can be derived using pythagoras's theorem. The length of the light clock is l. According to the observer's clocks, the clock in the light clock travels longer (l' = ct'). Horizontal distance traveled by the light clock: vt'. t = l/c
l2+(vt')2 = (l')2
t'2 = (l')2/c2
t'2 = (l2+(vt')2)/(c2)
After rearranging, t' = 1/( 1-v2/(c2) ) x t
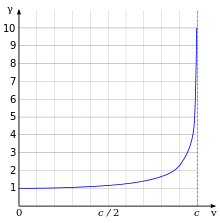
H.3.4 Sketch and annotate a graph showing the variation with relative velocity of the Lorentz factor
[edit | edit source]H.3.5 Solve problems involving time dilation
[edit | edit source]H.3.6 Define proper length
[edit | edit source]Length of an object as defined in a reference frame which is in rest with the object (inertial reference frame)
H.3.7 Describe the phenomenon of length contraction
[edit | edit source]H.3.8 Solve problems involving length contraction
[edit | edit source]H.4 Some consequences of special relativity
[edit | edit source]H.4.1. Describe how the concept of time dilation leads to the "twin paradox"
[edit | edit source]H.4.2 Discuss the Hafele-Keating experiment
[edit | edit source]Testing the theory of special relativity, scientists flew two clocks around the world in opposite directions and compared them to a clock that was stationary relative to the earth's surface. One plane flew eastward and another went westward. When the planes returned, it was found that that for the plane flying East, it's clock was slower than the clock on the earth's surface (it was behind by 59 ns). Since the earth spins to the east and the plane was travelling east relative to the earth's atmosphere, this clock had a greater velocity relative to the stationary frame of reference: the centre of the Earth and so it's clock ticked a little slower. The westward clock ran faster than the clock that remained on the earth's surface as it was moving more slowly relative to the centre of the earth. This experiment provided evidence of time dilation that was in excellent agreement with relativistic predictions.
H.4.3 Solve one-dimensional problems involving the relativistic addition of velocities
[edit | edit source]H.4.4 State the formula representing the equivalence of mass and energy
[edit | edit source]H.4.5 Define rest mass
[edit | edit source]Rest mass of an object is defined to be the energy required to produce the object at rest.
H.4.6 Distinguish between the energy of a body at rest and its total energy when moving
[edit | edit source]H.4.7 Explain why no object can ever attain the speed of light in a vacuum
[edit | edit source]According to the classical mechanics, F = ma therefore if the force is applied to an object constantly over a very long time period, the speed of the object must increase without limit. However, this is not true; as the speed of the object increases, the relativistic mass of the object increases, therefore acceleration will gradually decrease. Only the particles with no rest mass (such as photon) can travel with the speed of light.
H.4.8 Determine the total energy of an accelerated particle
[edit | edit source]The total energy E, momentum p, and the rest energy E0 (=m0c2) have a relationship E2 = p2c2 + E02.
H.5 Evidence to support special relativity
[edit | edit source]H.5.1 Discuss muon decay as experimental evidence to support special relativity
[edit | edit source]H.5.2 Solve problems involving the muon decay experiment
[edit | edit source]H.5.3 Outline the Michelson-Morley experiment
[edit | edit source]H.5.4 Discuss the result of the Michelson-Morley experiment and its implication
[edit | edit source]H.5.5 Outline an experiment that indicates that the speed of light in vacuum is independent of its source
[edit | edit source]H.6 Relativistic momentum and energy
[edit | edit source]H.6.1 Apply the relation for the relativistic momentum p = γm0u of particles
[edit | edit source]H.6.2 Apply the formula Ek = (γ-1)m0c2 for the kinetic energy of a particle
[edit | edit source]H.6.3 Solve problems involving relativistic momentum and energy
[edit | edit source]H.7 General relativity
[edit | edit source]H.7.1 Explain the difference between the terms gravitational mass and inertial mass
[edit | edit source]Gravitational mass is the mass obtained from when a gravitational force acts upon an object. The inertial mass is the mass obtained from when an external force acts upon a body (the mass is resisting the acceleration). Evidently, the gravitational and inertial mass are exactly the same because uniform acceleration is indistinguishable from a gravitational field.
H.7.2 Describe and discuss Einstein's principle of equivalence
[edit | edit source]The principle of equivalence states that there is no difference between an accelerating observer and an observer in a gravitational field. This principle coincides with General Relativity and the IB exams focus on light being bent by a gravitational field; Einstein stated this idea in respect to his closed elevator thought experiment. Light bent the same way regardless of whether the elevator was at rest or accelerating downward. The second part of the principle of equivalence is that time slows down when an object approaches a massive body such as black holes.
H.7.3 Deduce that the principle of equivalence predicts bending of light rays in a gravitational field
[edit | edit source]H.7.4 Deduce that the principle of equivalence predicts that time slows down near a massive body
[edit | edit source]H.7.5 Describe the concept of spacetime
[edit | edit source]Spacetimeis the 4-dimensional world with three space and one time coordinates.
H.7.6 State that moving objects follow the shortest path between two points in spacetime
[edit | edit source]In the absence of any forces, a moving object will move in spacetime along path with the shortest length. This path is called geodesics.
H.7.7 Explain gravitational attraction in terms of the warping of spacetime by matter
[edit | edit source]Large masses will warp space-time in such a way that the shortest distance to be travelled between point A and B for a particle is now a curve around the large mass. As such, this curved path that the particle follows can be thought of as the gravitational attraction.
H.7.8 Describe black holes
[edit | edit source]Black hole is a singularity of space time, and is a point of infinite density. It causes extreme curvature of spacetime around it.
H.7.9 Define the term Schwarzschild radius
[edit | edit source]Schwarzschild radius (Rs) is sometimes called gravitational radius, or event horizon. Within Rs, no object can escape from the gravitational field (because the escape velocity exceeds c within Rs).
H.7.10 Calculate the Schwarzschild radius
[edit | edit source]Rs = 2GMc-2, where G is the gravitational constant and M is mass of the black hole (or the star).
H.7.11 Solve problems involving time dilation close to a black hole
[edit | edit source]H.7.12 Describe the concept of gravitational red-shift
[edit | edit source]H.7.13 Solve problems involving frequency shifts between different points in a uniform gravitational field
[edit | edit source]H.7.14 Solve problems using the gravitational time dilation formula
[edit | edit source]H.8 Evidence to support general relativity
[edit | edit source]H.8.1 Outline an experiment for the bending of EM waves by a massive object
[edit | edit source]H.8.2 Describe gravitational lensing
[edit | edit source]Assuming a massive galaxy has a large gravitational pull, light from a distant quasar is bent, thereby creating two quasars when viewed through a telescope. The galaxy acts a lens as it bends the incoming light from the quasar.
H.8.3 Outline an experiment that provides evidence for gravitational red-shift
[edit | edit source]Pound-Rebka Experiment where they shot a photon from the ground floor of a building up to the attic. They found that the frequency of the photon was longer up at the attic then at the ground floor and thus, provides evidence for gravitational red-shift.
