High School Trigonometry/Trigonometric Functions of Any Angle
In the previous lesson we introduced the six trigonometric functions, and we worked with these functions in two ways: first, in right triangles, and second, for angles of rotation. In this lesson we will extend our work with trig functions of angles of rotation to any angle in the unit circle, including negative angles, and angles greater than 360 degrees. In the previous lesson, we worked with the quadrantal angles, and with the angles 30°, 45°, and 60°. In this lesson we will work with angles related to these angles, as well as other angles in the unit circle. One of the key ideas of this lesson is that angles may share the same trig values. This idea will be developed throughout the lesson.
Learning Objectives
[edit | edit source]- Identify the reference angles for angles in the unit circle.
- Identify the ordered pair on the unit circle for angles whose reference angle is 30°, 45°, and 60°, or a quadrantal angle, including negative angles, and angles whose measure is greater than 360°.
- Use these ordered pairs to determine values of trig functions of these angles.
- Use tables and calculators to find values of trig functions of any angle.
Reference Angles and Angles in the Unit Circle
[edit | edit source]In the previous lesson, one of the review questions asked you to consider the angle 150°. If we graph this angle in standard position, we see that the terminal side of this angle is a reflection of the terminal side of 30°, across the y−axis.
Notice that 150° makes a 30° angle with the negative x−axis. Therefore we say that 30° is the reference angle for 150°. Formally, the reference angle of an angle in standard position is the angle formed with the closest portion of the x−axis. Notice that 30° is the reference angle for many angles. For example, it is the reference angle for 210° and for −30°.
In general, identifying the reference angle for an angle will help you determine the values of the trig functions of the angle.
|
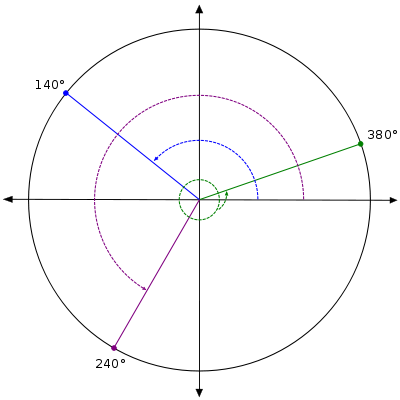
Example 1 Graph each angle and identify its reference angle. a. 140° b. 240° c. 380° Solution: a. 140° makes a 40° angle with the x-axis. Therefore the reference angle is 40°. b. 240° makes a 60° with the x-axis. Therefore the reference angle is 60°. c. 380° is a full rotation of 360°, plus an additional 20°. So this angle is co-terminal with 20°, and 20° is its reference angle. |
If an angle has a reference angle of 30°, 45°, or 60°, we can identify its ordered pair on the unit circle, and so we can find the values of the six trig functions of that angle. For example, above we stated that 150° has a reference angle of 30°. Because of its relationship to 30°, the ordered pair for is 150° is . Now we can find the values of the six trig functions of 150°:
|
Example 2 Find the ordered pair for 240° and use it to find the value of sin 240°. Solution: sin(240°) = As we found in example 1, the reference angle for 240° is 60°. The figure below shows 60° and the three other angles in the unit circle that have 60° as a reference angle. The terminal side of the angle 240° represents a reflection of the terminal side of 60° over both axes. So the coordinates of the point are . The y coordinate is the sine value, so sin(240°) = . |
Just as the figure above shows 60° and three related angles, we can make similar graphs for 30° and 45°.
|
Example 3 Find the value of cot(300°). Solution: cot(300°) = Using the graph above, you will find that the ordered pair is . Therefore the cotangent value is
|
We can also use the concept of a reference angle and the ordered pairs we have identified to determine the values of the trig functions for other angles.
Trigonometric Functions of Negative Angles
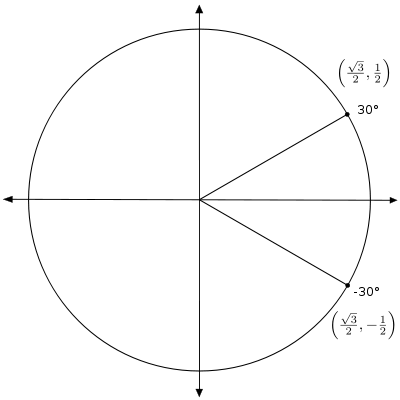
[edit | edit source]Recall that graphing a negative angle means rotating clockwise. The graph below shows -30°.
Notice that this angle is coterminal with 330°. So the ordered pair is . We can use this ordered pair to find the values of any of the trig functions of −30°. For example, cos(−30°) = x = .
In general if a negative angle has a reference angle of 30°, 45°, or 60°, or if it is a quadrantal angle, we can find its ordered pair, and so we can determine values of any of the trig functions of the angle.
|
Example 4 Find the value of each expression. a. sin(−45°) b. sec(−300°) c. cos(−90°) Solution: a. sin(−45°) = −45° is in the 4th quadrant, and has a reference angle of 45°. That is, this angle is coterminal with 315°. Therefore the ordered pair is and the sine value is . b. sec(-300°) = 2 The angle −300° is in the 1st quadrant and has a reference angle of 60°. That is, this angle is coterminal with 60°. Therefore the ordered pair is and the secant value is 2. c. cos(−90°) = 0 The angle −90° is coterminal with 270°. Therefore the ordered pair is (0, −1) and the cosine value is 0. |
We can also use our knowledge of reference angles and ordered pairs to find the values of trig functions of angles with measure greater than 360 degrees.
Trigonometric Functions of Angles Greater than 360 Degrees
[edit | edit source]Consider the angle 390°. As you learned previously, you can think of this angle as a full 360 degree rotation, plus an additional 30 degrees. Therefore 390° is coterminal with 30°. As you saw above with negative angles, this means that 390° has the same ordered pair as 30°, and so it has the same trig values. For example, cos(390°) = cos(30°) = :
In general, if an angle whose measure is greater than 360 has a reference angle of 30°, 45°, or 60°, or if it is a quadrantal angle, we can find its ordered pair, and so we can find the values of any of the trig functions of the angle. The first step is to determine the reference angle.
|
Example 5 Find the value of each expression. a. sin(420°) b. tan(840°) c. cos(540°) Solution: a. sin(420°) = 420° is a full rotation of 360 degrees, plus an additional 60 degrees. Therefore the angle is coterminal with 60°, and so it shares the same ordered pair, . The sine value is the y coordinate. b. tan(840°) = −√3 840° is two full rotations, or 720 degrees, plus an additional 120 degrees:
Therefore 840° is coterminal with 120°, so the ordered pair is . The tangent value can be found by the following: c. cos(540°) = −1 540° is a full rotation of 360 degrees, plus an additional 180 degrees. Therefore the angle is coterminal with 180◦, and the ordered pair is (−1, 0). So the cosine value is −1. |
So far all of the angles we have worked with are multiples of 30, 45, 60, and 90. Next we will find approximate values of the trig functions of other angles.
Trigonometric Function Values in Tables
[edit | edit source]As you work through this chapter, you will learn about different applications of the trig functions. In many cases, you will need to find the value of a function of an angle that is not necessarily one of the "special" angles we have worked with so far. Traditionally, textbooks have provided students with tables that contain values of the trig functions. Below is a table that provides approximate values of the sine, cosine, and tangent values of several angles.
Table 1.11 Angle (°) Cosine Sine Tangent 0 1.000 0.000 0.000 5 0.9962 0.0872 0.0875 10 0.9848 0.1736 0.1763 15 0.9659 0.2588 0.2679 20 0.9397 0.3420 0.3640 25 0.9063 0.4226 0.4663 30 0.8660 0.5000 0.5774 35 0.8192 0.5736 0.7002 40 0.7660 0.6428 0.8391 45 0.7071 0.7071 1.0000 50 0.6428 0.7660 1.1918 55 0.5736 0.8192 1.4281 60 0.5000 0.8660 1.7321 65 0.4226 0.9063 2.1445 70 0.3420 0.9397 2.7475 75 0.2588 0.9659 3.7321 80 0.1736 0.9848 5.6713 85 0.0872 0.9962 11.4301 90 0.0000 1.0000 undefined 95 −0.0872 0.9962 −11.4301 100 −0.1736 0.9848 −5.6713 105 −0.2588 0.9659 −3.7321 110 −0.3420 0.9397 −2.7475 115 −0.4226 0.9063 −2.1445 120 −0.5000 0.8660 −1.7321 125 −0.5736 0.8192 −1.4281 130 −0.6428 0.7660 −1.1918 135 −0.7071 0.7071 −1.0000 140 −0.7660 0.6428 −0.8391 145 −0.8192 0.5736 −0.7002 150 −0.8660 0.5000 −0.5774 155 −0.9063 0.4226 −0.4663 160 −0.9397 0.3420 −0.3640 165 −0.9659 0.2588 −0.2679 170 −0.9848 0.1736 −0.1763 175 −0.9962 0.0872 −0.0875 180 −1.0000 0.0000 0.0000
We can use the table to identify approximate values.
|
Example 6 Find the approximate value of each expression, using the table above. a. sin(130°) b. cos(15°) c. tan(50°) Solution: a. sin(130°) ≈ 0.7660 We can identify the sine value by finding the row in the table for 130 degrees. The sine value is found in the third row of the table. Note that this is an approximate value. We can evaluate the reasonableness of this value by thinking about an angle that is close to 130 degrees, 120 degrees. We know that the ordered pair for 120 is , so the sine value is ≈ 0.8660, which is also in the table. It is reasonable that sin(130°) ≈ 0.7660, which is slightly less than the sine value of 120°, given where the terminal sides of these angles intersect the unit circle. b. cos(15°) ≈ 0.9659 We can identify this cosine value by finding the row for 15 degrees. The cosine value is found in the second column. Again, we can determine if this value is reasonable by considering a nearby angle. 15° is between 0° and 30°, and its cosine value is between the cosine values of these two angles. c. tan(50°) ≈ 1.1918 We can identify this tangent value by finding the row for 50 degrees, and reading the final column of the table. In the review questions, you will be asked to explain why the tangent value seems reasonable. |
Using a Calculator to Find Values
[edit | edit source]If you have a scientific calculator, you can determine the value of any trig function for any angle. Here we will focus on using a TI graphing calculator to find values.
First, your calculator needs to be in the correct "mode". In chapter 2 you will learn about a different system for measuring angles, known as radian measure. In this chapter, we are measuring angles in degrees. (This is analogous to measuring distance in miles or in kilometers. It's just a different system of measurement.) We need to make sure that the calculator is working in degrees. To do this, press [MODE]. You will see that the third row says Radian Degree. If Degree is highlighted, you are in the correct mode. If Radian is highlighted, scroll down to this row, scroll over to Degree, and press [ENTER]. This will highlight Degree. Then press 2nd [MODE] to return to the main screen.
Now you can calculate any value. For example, we can verify the values from the table above. To find sin(130°), press [SIN] [1] [3] [0] [ENTER]. The calculator should return the value .7660444431.
You may have noticed that the calculator provides a "(" after the SIN. In the previous calculation, you can actually leave off the ")". However, in more complicated calculations, leaving off the closing ")" can create problems. It is a good idea to get in the habit of closing parentheses.
You can also use a calculator to find values of more complicated expressions.
|
Example 7 Use a calculator to find an approximate value of sin(25°) + cos(25°). Round your answer to 4 decimal places. Solution: sin(25°) + cos(25°) ≈ 1.3289 To use a TI graphing calculator, press [SIN] [25] [+] [COS] [2] [5] [ENTER]. The calculator should return the number 1.328926049. This rounds to 1.3289. |
Lesson Summary
[edit | edit source]In this lesson we have examined the idea that we can find an exact or an approximate value of each of the six trig functions for any angle. We began by defining the idea of a reference angle, which is useful for finding the ordered pair for certain angles in the unit circle. We have found exact values of the trig functions for "special" angles, including negative angles, and angles whose measures are greater than 360 degrees. We have also found approximations of values for other angles, using a table, and using a calculator. In the coming lessons, we will use the ideas from this lesson to (1) examine relationships among the trig functions and (2) apply trig functions to real situations.
Points to Consider
[edit | edit source]- What is the difference between the measure of an angle, and its reference angle? In what cases are these measures the same value?
- Which angles have the same cosine value, or the same sine value? Which angles have opposite cosine and sine values?
Review Questions
[edit | edit source]- State the reference angle for each angle.
- (a) 190°
- (b) −60°
- (c) 1470°
- (d) −135°
- State the ordered pair for each angle.
- (a) 300°
- (b) −150°
- (c) 405°
- Find the value of each expression.
- (a) sin(210°)
- (b) tan(270°)
- (c) csc(120°)
- Find the value of each expression.
- (a) sin(510°)
- (b) cos(930°)
- (c) csc(405°)
- Find the value of each expression.
- (a) cos(−150°)
- (b) tan(−45°)
- (c) sin(−240°)
- Use the table in the lesson to find an approximate value of cos(100°).
- Use the table in the lesson to approximate the measure of an angle whose sine value is 0.2.
- In example 6c, we found that tan(50°) ≈ 1.1918. Use your knowledge of a special angle to explain why this value is reasonable.
- Use a calculator to find each value. Round to 4 decimal places.
- (a) sin(118°)
- (b) tan(55°)
- Use the table below or a calculator to explore sum and product relationships among trig functions.
- Consider the following functions:
- f(x) = sin(x+x) and g(x) = sin(x) + sin(x)
- h(x) = sin(x) · sin(x) and j(x) = sin(x2)
- Do you observe any patterns in these functions? Are there any equalities among the functions? Can you make a general conjecture about sin(a) + sin(b) and sin(a+b) for all values of a, b?
- What about sin(a) · sin(a) and sin(a2)?
a° b° sin a + sin b sin(a+b) 10 30 0.6736 0.6428 20 60 1.2080 0.9848 55 78 1.7973 0.7314 122 25 1.2707 0.5446 200 75 0.6239 −0.9962
- Consider the following functions:
- Use a calculator or your knowledge of special angles to fill in the values in the table, then use the values to make a conjecture about the relationship between (sin a)2 and (cos a)2. If you use a calculator, round all values to 4 decimal places.
a (sin a)2 (cos a)2 0 25 45 80 90 120 250
Review Answers
[edit | edit source]-
- (a) 10°
- (b) 60°
- (c) 30°
- (d) 45°
-
- (a)
- (b)
- (c)
-
- (a)
- (b) undefined
- (c)
-
- (a)
- (b)
- (c) √2
-
- (a)
- (b) −1
- (c)
- −0.1736
- Between 165 and 160 degrees.
- This is reasonable because tan(45°) = 1 .
-
- (a) 0.8828
- (b) 1.4281
- Conjecture: sin a + sin b ≠ sin(a+b) .
- Conjecture: (sin a)2 + (cos a)2 = 1 .
a (sin a)2 (cos a)2 0 0 1 25 0.1786 0.8216 45 0.5000 0.5000 80 0.9698 0.0302 90 1 0 120 0.7500 0.2500 250 0.8830 0.1170
Vocabulary
[edit | edit source]- coterminal angles
- Two angles in standard position are coterminal if they share the same terminal side.
- reference angle
- The reference angle of an angle in standard position is the measure of the angle between the terminal side and the closest portion of the x−axis.
This material was adapted from the original CK-12 book that can be found here. This work is licensed under the Creative Commons Attribution-Share Alike 3.0 United States License