High School Trigonometry/Radian Measure
In this lesson you will be introduced to the radian as a common unit of angle measure in trigonometry. It is important that you become proficient converting back and forth between degrees and radians. Eventually, much like learning a foreign language, you will become comfortable with radian measure when you can learn to "think" in radians instead of always converting from degree measure. Finally, we will review the calculations of the basic trigonometry functions of angles based on 30, 45, and 60 degree rotations.
Learning Objectives
[edit | edit source]- Define radian measure.
- Convert angle measure from degrees to radians and from radians to degrees.
- Calculate the values of the six trigonometric functions for special angles in terms of radians or degrees.
Understanding Radian Measure
[edit | edit source]Many units of measure come from seemingly arbitrary and archaic roots. Some even change over time. The meter, for example was originally intended to be based on the circumference of the earth and now has an amazingly complicated scientific definition based on the number of cycles (wavelengths) of a specific frequency of coherent light! We typically use degrees to measure angles, as we do seconds to minutes and minutes to hours. All multiples of 60 and 12, which the Western Civilizations got handed down from the Ancient Sumerian Empires base sixty number system invented a mere 60 centuries ago, more or less—back when the fashionable scene was the Cradle of Civilization, and most tribes were nomads barely getting by without starving.
Exactly what is a degree? A degree is 1/360th of a complete rotation around a circle. Radians are alternate units used to measure angles in trigonometry, and sometimes referred to as Natural Angles. Let's see why that might be.
Just as it sounds, a radian is based on the radius of a circle. It turns out, precisely One radian is the angle created by bending the unit-radius' length (arc's length) around the arc of a unit circle. One radian's rotation, one radius the same radian's length, and one radian's length of arc traced—this is in fact the 'arc length of a one radian segment of a circle'. Turn it on its head: assume a length, make a circle with that radius, call that unitary (one or base), and measure the same length around the rim. No matter what the length, that angle will always be a radian.
Is there another reason it might be called a natural angle, perhaps one related to the TRI (which means THREE) in TRIGONOMETRY, our study subject? By the way, you've probably heard of the constant PI ('π') and may even know it is approximately 3.1459 somethings. What somethings?{{efn|On the History of PI ('π') Would you guess, 3.1459 radians, and be correct? Let's see by units analysis and see what cancels and what stays. Deducing from the above, might we not write:
Segment (length) = Angle (radians) ⋅ length of Radius) ⇔ s = (∅ ⋅ r), where 's' is a common variable of arc length, so for the equation to balance with length as the units, radians must be [ 1/(length/rotation angle) ]—which devolves to rotation angle Because a radian is based on an actual part of the circle rather than an arbitrary division, it is a much more natural unit of angle measure for upper level mathematics and will be especially useful when you move on to study calculus.
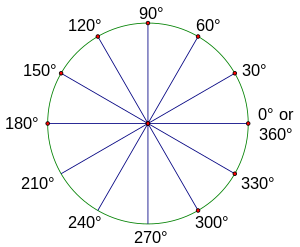
What if we were to rotate all the way around the circle? Continuing to add radius lengths, we find that it takes a little more than 6 of them to complete the rotation.
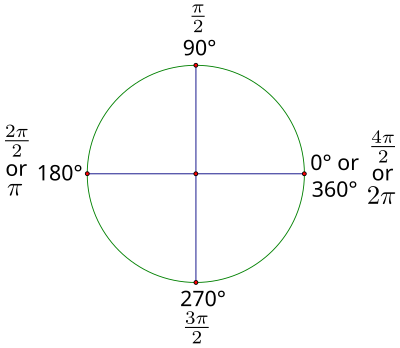
But the arc length of a complete rotation is really the circumference! The circumference is equal to the 2π times the length of the radius. 2π is approximately 6.28, so the circumference is a little more than 6 radius lengths. Or, in terms of radian measure, a complete rotation (360 degrees) is 2π radians.
With this as our starting point, we can find the radian measure of other angles easily. Half of a rotation, or 180 degrees, must therefore be π radians, and 90 degrees must be one-half pi. Complete the table below:
| Angle in Degrees | Angle in Radians |
|---|---|
| 90 | |
| 45 | |
| 30 | |
| 60 | |
| 75 |
Because 45 is half of 90, half of one-half π is one-fourth π. 30 is one-third of a right angle, so multiplying gives:
and because 60 is twice as large as 30:
Here is the completed table:
| Angle in Degrees | Angle in Radians |
|---|---|
| 90 | |
| 45 | |
| 30 | |
| 60 | |
| 75 |
The last value was found by adding the radian measures of 30 and 45:
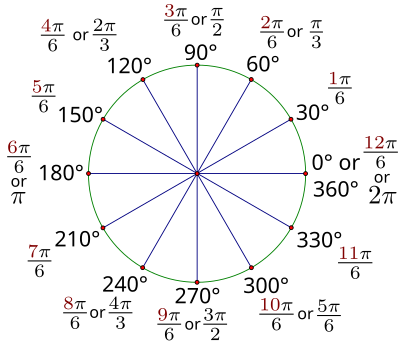
There is a formula to help you convert between radians and degrees that you may already have discovered and we will discuss shortly, however, most angles that you will commonly use can be found easily from the values in this table, so learning them based on the circumference should help increase your comfort level with radians greatly. For example, most students find it easy to remember 30 and 60. 30 is π over 6 and 60 is π over 3. If you know these angles, you can find any of the special angles that have reference angles of 30 and 60 because they will all have the same denominators. The same is true of multiples of pi over 4 (45 degrees) and pi over 2 (90 degrees).
"Count"ing in Radians
[edit | edit source]Do you remember as a child watching the Count on Sesame Street? He would count objects like apples, "one apple, two apples, three apples…" and then laugh fiendishly as lightning and thunder erupted around him. Well, to be successful with radian measure, you need to learn to count all over again using radians instead of apples. Let's start counting right angles, which are really radians.
- "one π over 2, two π over 2 (really just π), three π over 2, four π over 2 (which is really 2π)"
 |
| Figure 2.1: 90-degree rotations expressed in radian measure. |
You just covered all the angles that are multiples of 90 degrees in one rotation.
Here is the drawing for 45-degree angles:
 |
| Figure 2.2: 45-degree rotations. |
Notice that the additional angles in the drawing all have reference angles of 45 degrees and their radian measures are all multiples of . Complete the following radian measures by counting in multiples of and :
|
|
 |
| Figure 2.5: 60-degree reference angle radian measure through one rotation. |
 |
| Figure 2.6: 30-degree reference angle radian measure through one rotation. |
Notice that all of the angles with 60-degree reference angles are multiples of , and all of those with 30-degree reference angles are multiples of If you can learn to count in these terms, rather than constantly having to convert back to degrees, it will help you to be effective dealing with most radian measures that you will encounter.
For other examples there is a formula. Remember that:
If you divide both sides of this equality by 180 you will uncover the formula for easy conversion:
so
If we have a degree measure and wish to convert it to radians, then manipulating the equation above gives:
|
Example 1 Convert to degree measure. Solution: Well, if you followed the last section, you should recognize that this angle is a multiple of (or 60 degrees), so there are 11 individual 's in this angle: · 11 = 60 · 11 = 660°. Here is what it would look like using the formula: |
|
Example 2 Convert −120° to radian measure. Leave the answer in terms of π. Solution: Using the formula: and reducing to lowest terms gives: However, you could also realize that 120 is 2 · 60. Since 60° is radians, then 120 is 2 individual 's, or . Make it negative and you have the answer, −. |
|
Example 3 Express radians in degree measure. Solution: |
Radians, Degrees, and a Calculator
[edit | edit source]Most scientific and graphing calculators have a [MODE] setting that will allow you to either convert between radians and degrees, or to find approximations for trig functions using either measure. It is important that if you are using your calculator to estimate a trig function that you know which mode you are using. Look at the following screen:
If you entered this expecting to find the sine of 30 degrees you would realize based on the last chapter that something is wrong because it should be . In fact, as you may have suspected, the calculator is interpreting this as 30 radians. In this case, changing the mode to degrees and recalculating we give the expected result.
Scientific calculators will usually have a 3−letter display that shows either DEG or RAD to tell you which mode you are in. Always check before calculating a trig ratio!
|
Example 4 Find the tangent of . Solution: First of all, shame on you if you are using a calculator to find this answer! You should know this one! is a 2nd quadrant angle with a reference angle of (45 degrees). The tangent of is 1, and because tangent is negative in quadrant II, the answer is −1. To verify this on your calculator, make sure the mode is set to radians, and evaluate the tangent of .
tan(3π/4)
-1
|
|
Example 5 Find the value of cos to four decimal places. Solution: Again, you should know the exact value based on your previous work. has a reference angle of (30 degrees) and the sign of is . Because is in the 4th quadrant, the cosine is positive and so the exact answer is . Using the calculator gives:
cos(11π/6)
.8660254038
Which, when rounded, is 0.8660. You can verify that it is indeed a very good approximation of our exact answer using your calculator as well.
cos(11π/6)
.8660254038
√(3)/2.8660254038
|
|
Example 6 Convert 1 radian to degree measure. Solution: Many students get so used to using π in radian measure that they incorrectly think that 1 radian means 1π radians. While it is more convenient and common to express radian measure in terms of π, don't lose sight of the fact that π radians is actually a number! It specifies an angle created by a rotation of approximately 3.14 radius lengths. So 1 radian is a rotation created by an arc that is only a single radius in length. Look back at Figure 1.1. What would you estimate the degree measure of this angle to be? It is certainly acute and appears similar to a 60° angle. To find a closer approximation, we will need the formula and a calculator. So 1 radian would be degrees. Using any scientific or graphing calculator will give a reasonable approximation for this degree measure, approximately 57.3°.
180/π
57.29577951
|
|
Example 7 Find the radian measure of an acute angle θ with a sin θ = 0.7071. Solution: First of all, it is important to understand that your calculator will most likely not give you radian measure in terms of π, but a decimal approximation instead. In this case you need to use the inverse sine function.
sin-1(.7071)
.7853885734
This answer may not look at all familiar, but 0.7071 may sound familiar to you. It is an approximation of . So, as you may know, this is really a 45° angle. Sure enough, evaluating will show that the calculator is giving its best approximation of the radian measure.
sin-1(.7071)
.7853885734
π/4.7853981634
If it bothers you that they are not exactly the same, good, it should! Remember that 0.7071 is only an approximation of , so we are already starting off with some rounding error. |
Lesson Summary
[edit | edit source]Angles can be measured in degrees or radians. A radian is the angle defined by an arc length equal to the radius length bent around the circle. One complete rotation around a circle, or 360° is equal to 2π radians. To convert from degrees to radians you use the following formula:
To convert from radians to degrees the formula becomes:
Much like learning a foreign language where you have to memorize vocabulary to be successful, it will be very helpful for you to understand and be able to communicate in radian measure if you become familiar with the radian measures of the quadrant angles (90° = , 180° = π, 270° = , 360° = 2π) and special angles (30° = , 45° = , 60° = ).
Review Questions
[edit | edit source]
- The picture to the right is a sign for a store that sells cheese.
- (a) Estimate the degree measure of the angle of the circle that is missing.
- (b) Convert the measure to radians.
- (c) What is the radian measure of the part of the cheese that remains?
- Convert the following degree measures to radians. Give exact answers in terms of π, not decimal approximations.
- (a) 240°
- (b) 270°
- (c) 315°
- (d) −210°
- (e) 120°
- (f) 15°
- (g) −450°
- (h) 72°
- (i) 720°
- (j) 330°
- Convert the following radian measures to degrees:
- (a)
- (b)
- (c)
- (d)
- (e)
- (f)
- (g)
- (h)
- (i)
- (j)
- The drawing shows all the quadrant angles as well as those with reference angles of 30°, 45°, and 60°. On the inner circle, label all angles with their radian measure in terms of π and on the outer circle, label all the angles with their degree measure.

- Using a calculator, find the approximate degree measure (to the nearest tenth) of each angle expressed in radians.
- (a)
- (b) 1 radian
- (c) 3 radians
- (d)
- Gina wanted to calculate the sin of 210 and got the following answer on her calculator:
- sin(210).4677185183
- (a) Write the correct answer.
- (b) Explain what she did wrong.
- Complete the following chart. Write your answers in simplest radical form.
x sin(x) cos(x) tan(x)
Review Answers
[edit | edit source]-
- (a) Answer may vary, but 120° seems reasonable.
- (b) Based on the answer in part a, the rational answer would be
- (c) Again, based on part a,
-
- (a)
- (b)
- (c)
- (d)
- (e)
- (f)
- (g)
- (h)
- (i)
- (j)
-
- (a) 90°
- (b) 396°
- (c) 120°
- (d) 540°
- (e) 630°
- (f) 54°
- (g) 75°
- (h) −210°
- (i) 1440°
- (j) 48°

-
- (a) 154.3°
- (b) 57.3°
- (c) 171.9°
- (d) 327.3°
-
- (a) The correct answer is
- (b) Her calculator was in the wrong mode and she calculated the sine of 210 radians.
x sin(x) cos(x) tan(x) 1 0 undefined −1 0 undefined
This material was adapted from the original CK-12 book that can be found here. This work is licensed under the Creative Commons Attribution-Share Alike 3.0 United States License