High School Trigonometry/Applications of Right Triangle Trigonometry

In this lesson we will return to right triangle trigonometry. Many real situations involve right triangles. In your previous study of geometry you may have used right triangles to solve problems involving distances, using the Pythagorean Theorem. In this lesson you will solve problems involving right triangles, using your knowledge of angles and trigonometric functions. We will begin by solving right triangles, which means identifying all the measures of all three angles and the lengths of all three sides of a right triangle. Then we will turn to several kinds of problems.

Learning Objectives

Solve right triangles.
Solve real world problems that require you to solve a right triangle.

Solving Right Triangles

You can use your knowledge of the Pythagorean Theorem and the six trigonometric functions to solve a right triangle. Because a right triangle is a triangle with a 90 degree angle, solving a right triangle requires that you find the measures of one or both of the other angles. How you solve will depend on how much information is given. The following examples show two situations: a triangle missing one side, and a triangle missing two sides.

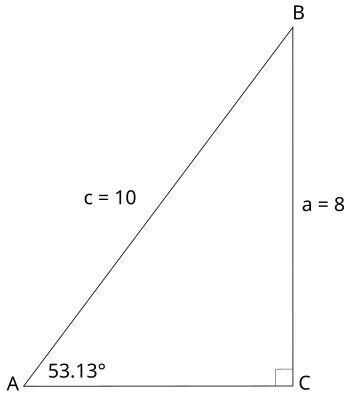
Example 1

Solve the triangle shown below.

Solution:

We need to find the lengths of all sides and the measures of all angles. In this triangle, two of the three sides are given. We can find the length of the third side using the Pythagorean Theorem:

$8^{2}+b^{2}=\,\!$	$10^{2}\,\!$
$64+b^{2}=\,\!$	$100\,\!$
$b^{2}=\,\!$	$36\,\!$
$b=\,\!$	$\pm 6\Rightarrow b=6\,\!$

(You may have also recognized the "Pythagorean Triple", 6, 8, 10, instead of carrying out the Pythagorean Theorem.)

You can also find the third side using a trigonometric ratio. Notice that the missing side, b, is adjacent to angle A, and the hypotenuse is given. Therefore we can use the cosine function to find the length of b:

$\cos(53.13^{\circ })=\,\!$	${\frac {\text{adjacent side}}{\text{hypotenuse}}}={\frac {b}{10}}$
$0.6=\,\!$	${\frac {b}{10}}$
$b=\,\!$	$0.6(10)=6\,\!$

We could also use the tangent function, as the opposite side was given. It may seem confusing that you can find the missing side in more than one way. The point is, however, not to create confusion, but to show that you must look at what information is missing, and choose a strategy. Overall, when you need to identify one side of the triangle, you can either use the Pythagorean Theorem, or you can use a trig ratio.

To solve the above triangle, we also have to identify the measures of all three angles. Two angles are given: 90 degrees and 53.13 degrees. We can find the third angle using the triangle angle sum:

180 − 90 − 53.13 = 36.87°

Now let's consider a triangle that has two missing sides.

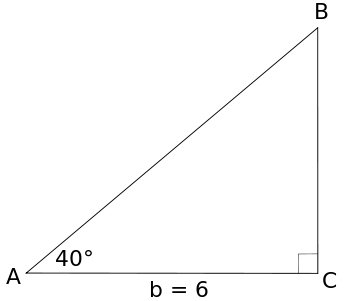
Example 2

Solve the triangle shown below.

Solution: In this triangle, we need to find the lengths of two sides. We can find the length of one side using a trig ratio. Then we can find the length of the third side either using a trig ratio, or the Pythagorean Theorem.

We are given the measure of angle A, and the length of the side adjacent to angle A. If we want to find the length of the hypotenuse, c, we can use the cosine ratio:

$\cos(40^{\circ })=\,\!$	${\frac {\text{adjacent}}{\text{hypotenuse}}}={\frac {6}{c}}$
$\cos(40^{\circ })=\,\!$	${\frac {6}{c}}$
$c\cos(40^{\circ })=\,\!$	$6\,\!$
$c=\,\!$	${\frac {6}{\cos(40^{\circ })}}\approx 7.83$

If we want to find the length of the other leg of the triangle, we can use the tangent ratio. (Why is this a better idea than to use the sine?)

$\tan(40^{\circ })=\,\!$	${\frac {\text{opposite}}{\text{adjacent}}}={\frac {a}{6}}$
$\tan(40^{\circ })=\,\!$	${\frac {a}{6}}$
$a=\,\!$	$6\tan(40^{\circ })\approx 5.03\,\!$

Now we know the lengths of all three sides of this triangle. In the review questions, you will verify the values of c and a using the Pythagorean Theorem. Here, to finish solving the triangle, we only need to find the measure of angle B:

180 − 90 − 40 = 50°

Notice that in both examples, one of the two non-right angles was given. If neither of the two non-right angles is given, you will need new strategy to find the angles. You will learn this strategy in chapter 4.

Angles of Elevation and Depression

You can use right triangles to find distances, if you know an angle of elevation or an angle of depression. The figure below shows each of these kinds of angles.

The angle of elevation is the angle between the horizontal line of sight and the line of sight up to an object. For example, if you are standing on the ground looking up at the top of a mountain, you could measure the angle of elevation. The angle of depression is the angle between the horizontal line of sight and the line of sight down to an object. For example, if you were standing on top of a hill or a building, looking down at an object, you could measure the angle of depression. You can measure these angles using a clinometer or a theodolite. People tend to use clinometers or theodolites to measure the height of trees and other tall objects. Here we will solve several problems involving these angles and distances.

Example 3

You are standing 20 feet away from a tree, and you measure the angle of elevation to be 38°. How tall is the tree?

Solution:

The solution depends on your height, as you measure the angle of elevation from your line of sight. Assume that you are 5 feet tall. Then the figure below shows the triangle you are solving.

The figure shows us that once we find the value of T, we have to add 5 feet to this value to find the total height of the triangle. To find T, we should use the tangent value:

$\tan(38^{\circ })=\,\!$	${\frac {\text{opposite}}{\text{adjacent}}}={\frac {T}{20}}$
$\tan(38^{\circ })=\,\!$	${\frac {T}{20}}$
$T=\,\!$	$20\tan(38^{\circ })\approx 15.63\,\!$
${\text{Height of tree}}\approx \,\!$	$20.63\ {\text{ft}}\,\!$

The next example shows an angle of depression.

Example 4

You are standing on top of a building, looking at park in the distance. The angle of depression is 53°. If the building you are standing on is 100 feet tall, how far away is the park? Does your height matter?

Solution:

If we ignore the height of the person, we solve the following triangle:

Given the angle of depression is 53°, angle A in the figure above is 37°. We can use the tangent function to find the distance from the building to the park:

$\tan(37^{\circ })=\,\!$	${\frac {\text{opposite}}{\text{adjacent}}}={\frac {d}{100}}$
$\tan(37^{\circ })=\,\!$	${\frac {d}{100}}$
$d=\,\!$	$100\tan(37^{\circ })\approx 75.36\ {\text{ft}}\,\!$

If we take into account the height if the person, this will change the value of the adjacent side. For example, if the person is 5 feet tall, we have a different triangle:

$\tan(37^{\circ })=\,\!$	${\frac {\text{opposite}}{\text{adjacent}}}={\frac {d}{105}}$
$\tan(37^{\circ })=\,\!$	${\frac {d}{105}}$
$d=\,\!$	$105\tan(37^{\circ })\approx 79.12\ {\text{ft}}\,\!$

If you are only looking to estimate a distance, than you can ignore the height of the person taking the measurements. However, the height of the person will matter more in situations where the distances or lengths involved are smaller. For example, the height of the person will influence the result more in the tree height problem than in the building problem, as the tree is closer in height to the person than the building is.

Right Triangles and Bearings

We can also use right triangles to find distances using angles given as bearings. In navigation, a bearing is the direction from one object to another. In air navigation, bearings are given as angles rotated clockwise from the north. The graph below shows an angle of 70 degrees:

It is important to keep in mind that angles in navigation problems are measured this way, and not the same way angles are measured in the unit circle. Further, angles in navigation and surveying may also be given in terms of north, east, south, and west. For example, N70° E refers to an angle from the north, towards the east, while N70° W refers to an angle from the north, towards the west. N70° E is the same as the angle shown in the graph above. N70° W would result in an angle in the second quadrant.

The following example shows how to use a bearing to find a distance.

Example 5

A ship travels on a N50° E course. The ship travels until it is due north of a port which is 10 nautical miles due east of the port from which the ship originated. How far did the ship travel?

Solution:

The angle opposite d is the complement of 50°, which is 40°. Therefore we can find d using the cosine function:

$\cos(40^{\circ })=\,\!$	${\frac {\text{adjacent}}{\text{hypotenuse}}}={\frac {10}{d}}$
$\cos(40^{\circ })=\,\!$	${\frac {10}{d}}$
$d\cos(40^{\circ })=\,\!$	$10\,\!$
$d=\,\!$	${\frac {10}{\cos(40^{\circ })}}\approx 13.05\ {\text{nm}}$

Other Applications of Right Triangles

In general, you can use trigonometry to solve any problem that involves right triangle. The next few examples show different situations in which a right triangle can be used to find a length or a distance.

Example 6

In lesson 3 we introduced the following situation: you are building a ramp so that people in wheelchairs can access a building. If the ramp must have a height of 8 feet, and the angle of the ramp must be about 5°, how long must the ramp be?

Given that we know the angle of the ramp and the length of the side opposite the angle, we can use the sine ratio to find the length of the ramp, which is the hypotenuse of the triangle:

$\sin(5^{\circ })=\,\!$	${\frac {8}{L}}$
$L\sin(5^{\circ })=\,\!$	$8\,\!$
$L=\,\!$	${\frac {8}{\sin(5^{\circ })}}\approx 91.8\ {\text{ft}}$

This may seem like a long ramp, but in fact a 5° ramp angle is what is required by the Americans with Disabilities Act (ADA). This explains why many ramps are comprised of several sections, or have turns. The additional distance is needed to make up for the small slope.

Right triangle trigonometry is also used for measuring distances that could not actually be measured. The next example shows a calculation of the distance between the moon and the sun. This calculation requires that we know the distance from the earth to the moon. In chapter 5 you will learn the Law of Sines, an equation that is necessary for the calculation of the distance from the earth to the moon. In the following example, we assume this distance, and use a right triangle to find the distance between the moon and the sun.

Example 7

The earth, moon, and sun create a right triangle during the first quarter moon. The distance from the earth to the moon is about 240,002.5 miles. What is the distance between the sun and the moon?

Solution:

Let d = the distance between the sun and the moon. We can use the tangent function to find the value of d:

$\tan(89.85^{\circ })=\,\!$	${\frac {d}{240,002.5}}$
$d=\,\!$	$240,002.5\tan(89.85^{\circ })=91,673,992.71\ {\text{miles}}$

Therefore the distance between the sun and the moon is much larger than the distance between the earth and the moon.

Lesson Summary

In this lesson we have returned to the topic of right triangle trigonometry, to solve real world problems that involve right triangles. To find lengths or distances, we have used angles of elevation, angles of depression, angles resulting from bearings in navigation, and other real situations that give rise to right triangles. In later chapters, you will extend the work of this chapter: you will learn to find missing angles using trig ratios, and you will learn how to determine the angles and sides of non-right triangles.

Points to Consider

In what kinds of situations do right triangles naturally arise?
Are there right triangles that cannot be solved?

Trigonometry can solve problems at astronomical scale as well as earthly even problems at a molecular or atomic scale. Why is this true?

Review Questions

Solve the triangle:
Two friends are writing practice problems to study for a trigonometry test. Sam writes the following problem for his friend Anna to solve:
In right triangle ABC, the measure of angle C is 90 degrees, and the length of side c is 8 inches. Solve the triangle.

Anna tells Sam that the triangle cannot be solved. Sam says that she is wrong. Who is right? Explain your thinking.
Use the Pythagorean Theorem to verify the sides of the triangle in example 2.
The angle of elevation from the ground to the top of a flagpole is measured to be 53°. If the measurement was taken from 15 feet away, how tall is the flagpole?
From the top of a hill, the angle of depression to a house is measured to be 14°. If the hill is 30 feet tall, how far away is the house?
An airplane departs city A and travels at a bearing of 100°. City B is directly south of city A. When the plane is 200 miles east of city B, how far has the plan traveled? How far apart are city A and City B?
The modern building shown below is built with an outer wall (shown on the left) that is not at a 90−degree angle with the floor. The wall on the right is perpendicular to both the floor and ceiling.

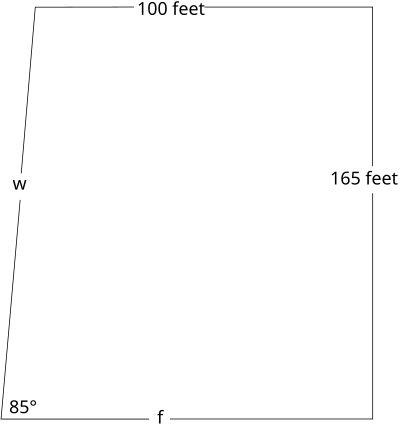
What is the length of the slanted outer wall, w? What is the length of the main floor, f?
A surveyor is measuring the width of a pond. She chooses a landmark on the opposite side of the pond, and measures the angle to this landmark from a point 50 feet away from the original point. How wide is the pond?
Find the length of side x:

Review Answers

$m\angle A=\,\!$	$58^{\circ }\,\!$
$b\approx \,\!$	$5.83\,\!$
$a\approx \,\!$	$9.33\,\!$

Anna is correct. There is not enough information to solve the triangle. That is, there are infinitely many right triangles with hypotenuse 8. For example:
6² + 5.03² = 36 + 25.3009 = 61.3009 = 7.83²
About 19.9 feet tall
About 120.3 feet
The plane has traveled about 203 miles. The two cities are 35 miles apart.
f ≈ 114.44 ft
w ≈ 188.83 ft
About 41.95 feet
About 7.44

Vocabulary

angle of depression: The angle between the horizontal line of sight, and the line of sight down to a given point.
angle of elevation: The angle between the horizontal line of sight, and the line of sight up to a given point.
bearings: The direction from one object to another, usually measured as an angle.
clinometer: A device used to measure angles of elevation or depression.
theodolite: A device used to measure angles of elevation or depression.
nautical mile: A nautical mile is a unit of length that corresponds approximately to one minute of latitude along any meridian. A nautical mile is equal to 1.852 kilometers.

← Relating Trigonometric Functions · Circular Functions →

This material was adapted from the original CK-12 book that can be found here. This work is licensed under the Creative Commons Attribution-Share Alike 3.0 United States License

f ≈	114.44 ft
w ≈	188.83 ft