High School Trigonometry/Angles in Triangles
The word trigonometry derives from two Greek words meaning triangle and measure. As you will learn throughout this chapter, trigonometry involves the measurement of angles, both in triangles, and in rotation (e.g, like the hands of a clock.) Given the important of angles in the study of trigonometry, in this lesson we will review some important aspects of triangles and their angles. We’ll begin by categorizing different kinds of triangles.
Learning Objectives
[edit | edit source]- Categorize triangles by their sides and angles.
- Determine the measures of angles in triangles using the triangle angle sum.
- Determine whether or not triangles are similar.
- Solve problems using similar triangles.
Triangles and Their Interior Angles
[edit | edit source]Formally, a triangle is defined as a 3−sided polygon. This means that a triangle has 3 sides, all of which are (straight) line segments. We can categorize triangles either by their sides, or by their angles. The table below summarizes the different types of triangles.
Table 1.6: Types of triangles Name Description Note Equilateral/equi-angular A triangle with three equal sides and three congruent angles. This type of triangle is acute Isosceles A triangle with two equal sides and two equal angles. An equilateral triangle is also isosceles. Scalene A triangle with no pairs of equal sides. Right A triangle with one 90° angle. It is not possible for a triangle to have more than one 90° angle (see below). Acute A triangle in which all three angles measure less than 90°. Obtuse A triangle in which one angle is greater than 90°. It is not possible for a triangle to have more than one obtuse angle (see below).
In the following example, we will categorize specific triangles.
|
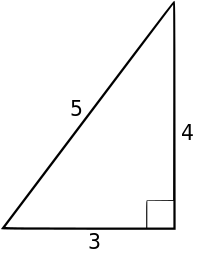
Example 1 Determine which category best describes the triangle: a. A triangle with side lengths 3, 7, and 8. b. A triangle with side lengths 5, 5, and 5. c. A triangle with side lengths 3, 4, and 5. Solution: a. This is a scalene triangle.
|
While there are different types of triangles, all triangles have one thing in common: the sum of the interior angles in a triangle is always 180°. You can see why this true if you remember that a straight line forms a "straight angle", which measures 180°. Now consider the diagram below, which shows the triangle ABC, and a line drawn through vertex B, parallel to side AC. Below the figure is a proof of the triangle angle sum.
- If we consider sides AB and CB as transversals between the parallel lines, then we can see that angle A and angle 1 are alternate interior angles.
- Similarly, angle C and angle 2 are alternate interior angles.
- Therefore angle A and angle 1 are congruent, and angle C and angle 2 are congruent.
- Now note that angles 1, 2, and B form a straight line. Therefore the sum of the three angles is 180°.
- We can complete the proof using substitution:
We can use this result to determine the measure of the angles of a triangle. In particular, if we know the measures of two angles, we can always find the third.
|
Example 3 Find the measures of the missing angles. a. A triangle has two angles that measures 30° and 50°. b. A right triangle has an angle that measures 30°. c. An isosceles triangle has an angle that measures 50°. Solution: a. 100° 180 - 30 - 50 = 100
The triangle is a right triangle, which means that one angle measures 90°. So we have: 180 − 90 − 30 = 60
There are two possibilities. First, if a second angle measures 50°, then the third angle measures 80° as 180 − 50 − 50 = 80. In the second case, the 50° angle is not one of the congruent angles. In this case, the sum of the other two angles is 180 − 50 = 130. Therefore the two angles each measure 65°. |
Notice that information about the angles of a triangle does not tell us the lengths of the sides. For example, two triangles could have the same three angles, but the triangles are not congruent. That is, the corresponding sides and the corresponding angles do not have the same measures. However, these two triangles will be similar. Next we define similarity and discuss the criteria for triangles to be similar.
Similar Triangles
[edit | edit source]Consider the situation in which two triangles have three pairs of congruent angles.
These triangles are similar. This means that the corresponding angles are congruent, and the corresponding sides are proportional. In the triangles shown above, we have the following:
- Three pairs of congruent angles:
- The ratios of sides within one triangle are equal to the ratios of sides within the second triangle:
- The ratios of corresponding sides are equal:
|
Example 4
|
Recall that these triangles are considered to be similar because they have three pairs of congruent angles. This is just one of three ways to determine that two triangles are similar. The table below summarizes criteria for determining if two triangles are similar.
A special case of SSS is "HL", or "hypotenuse leg". This is the case of two right triangles being similar. This case is examined in example 5 below.
|
Example 5 Determine if the triangles are similar. Solution: The triangles are similar. Recall that for every right triangle, we can use the Pythagorean Theorem to find the length of a missing side. In ABC we have:
Similarly, in triangle DEF we have:
Therefore the sides of the triangles are proportional, with a ratio of 2:1. |
Because we will always be able to use the Pythagorean Theorem in this way, two right triangles will be similar if the hypotenuse and one leg of one triangle are in proportion with the hypotenuse and one leg of the second triangle. This is the HL criteria.
Applications of Similar Triangles
[edit | edit source]Similar triangles can be used to solve problems in which lengths or distances are proportional. The following example will show you how to solve such problems.
|
Example 6 Use similar triangles to solve the problem: A tree casts a shadow that is 24 feet long. A person who is 5 feet tall is standing in front of the tree, and his shadow is 8 feet long. Approximately how tall is the tree? Solution: The picture shows us similar right triangles: the person and his shadow are the legs of one triangle, and the tree and its shadow form the legs of the larger triangle. The triangles are similar because of their angles: they both have a right angle, and they share one angle. Therefore the third angles are also congruent, and the triangles are similar. The ratio of the triangles' lengths is 3:1. If we let h represent the height of the tree, we have: |
Lesson Summary
[edit | edit source]In this lesson we have reviewed key aspects of triangles, including the names of different types of triangles, the triangle angle sum, and criteria for similar triangles. In the last example, we used similar triangles to solve a problem involving an unknown height. In general, triangles are useful for solving such problems, but notice that we did not use the angles of the triangles to solve this problem. This technique will be the focus of problems you will solve later in the chapter.
Points to Consider
[edit | edit source]- Why is it impossible for a triangle to have more than one right angle?
- Why is it impossible for a triangle to have more than one obtuse angle?
- How big can the measure of an angle get?
Review Questions
[edit | edit source]- Triangle ABC is an isosceles triangle. If side AB is 5 inches long, and side BC is 7 inches long, how long is side AC?
- Can a right triangle be an obtuse triangle? Explain.
- A triangle has one angle that measures 48° and a second angle that measures 28°. What is the measure of the third angle in the triangle?
- Claim: the two non-right angles in any right triangle are complements.
- In triangle DOG, the measure of angle O is twice the measure of angle D, and the measure of angle G is three times the measure of angle D. What are the measures of the three angles?
- Triangles ABC and DEF shown below are similar. What is the length of ?

- In triangles ABC and DEF above, if angle A measures 30°, what is the measure of angle E?
- Determine if the triangles are similar:
- A building casts a 100−foot shadow, while a 20 foot flagpole next to the building casts a 24 foot shadow. How tall is the building?
- Explain in your own words what it means for triangles to be similar.
Review Answers
[edit | edit source]- Either 5 inches or 7 inches.
- A right triangle cannot be an obtuse triangle. If a triangle is right triangle, one angle measures 90 degrees. If a triangle is obtuse, one angle measures greater than 90. Therefore the sum of the two angles would be greater than 180 degrees, which is not possible.
- 104°
-
- (a) The angle sum in the triangle is 180. If you subtract the 90−degree angle, you have 180 − 90 = 90 degrees, which is the sum of the remaining angles.
- (b) 90 − 23 = 67°
- 7.5
- 130°
-
- (a) No
- (b) Yes, by SSS or HL
- 83 ft
- Answers will vary. Responses should include (1) three pairs of congruent angles and (2) sides in proportion, or some other notion of "scaling up" or "scaling down".
Vocabulary
[edit | edit source]- acute angle
- An acute angle has a measure of less than 90 degrees.
- congruent
- Two angles are congruent if they have the same measure. Two segments are congruent if they have the same lengths.
- acute triangle
- A triangle with all acute angles.
- isosceles triangle
- A triangle with two congruent sides, and, consequentially, two congruent angles.
- equilateral triangle
- A triangle with all sides congruent, and, consequently, all angles congruent.
- scalene triangle
- A triangle with no pairs of sides congruent.
- leg
- One of the two shorter sides of a right triangle.
- hypotenuse
- The longest side of a right triangle, opposite the right angle.
- obtuse angle
- An angle that measures more than 90 degrees.
- parallel lines
- Lines that never intersect.
- right angle
- An angle that measures 90 degrees.
- transversal
- A line that intersects parallel lines.
This material was adapted from the original CK-12 book that can be found here. This work is licensed under the Creative Commons Attribution-Share Alike 3.0 United States License