High School Chemistry/Using Data
Earlier, we learned about qualitative and quantitative observations, and that with quantitative observations, we need measurements. In science, measurements mean data. In this upcoming section, we will delve deeper with data to look at patterns and to graph data. Sometimes we can graph the data, make calculations, sketch the line, and calculate the slope. All of these quantitative observations help us to formulate a conclusion that will be based on evidence.
Recognizing Patterns in the Data
[edit | edit source]As stated earlier, data can provide enormous information to scientists for making interpretations and drawing conclusions. In order for scientists to do this, they have to be able to look at a set of data and recognize patterns. Data can be in the form of pictures, charts, or graphs. Take for example, the picture found in (Figure 3.1). This, although not particularly chemistry related, has much to do with the concept of pattern recognition and the data gathered from these patterns. What do you believe scientists determined when first viewing this image prior to August 28, 2005?

Now, let us look at a common chemistry example. We all know that metals are supposed to be chemically reactive. How do we know that? Well, that is a property of metals. But how reactive are they? How can you tell? What do you know about the periodic table that would help you determine this right now? Look at Table 3.5 and see if you can gather a little evidence that can solidify your conclusions about the chemical reactivity of metals and the periodic table.
| Metal | Chemical Reactivity in Atmosphere |
|---|---|
| Sodium | Stored in toluene, extremely reactive |
| Potassium | Burns in O2 in seconds |
| Calcium | Slower to react with O2 than its neighbors to the right on the periodic table |
| Titanium | Resists corrosion after forming an oxide barrier |
| Aluminum | Resists corrosion after forming an oxide barrier |
| Gold | Does not react with oxygen |
| Platinum | Does not react with oxygen |
| Copper | Does not react with H2O; will react slowly with O2 |
| Iron | Rusts in O2 |

What kinds of conclusions can you make from reading this table? Can you determine that the reactions between the metals and the oxygen in the air decrease going across a row on the periodic table? Did you notice that the alkali (group one) metals (sodium and potassium) are the most reactive of all the metals with oxygen and the alkaline earth (group two) metals (calcium) are the second most reactive? Yes, they are. Aluminum as well as titanium will actually become coated with an oxide of their metals, which acts like a protective shield against further reaction. Look at the figure below. The copper has turned green as a result of this protective coating that formed on the copper rooftop. Have you ever seen this before?
The current Hotel Vancouver took over a decade to build during the 1930s as the Great Depression put a temporary halt to construction. It was Vancouver's tallest building from 1939 to 1972.
What kind of observations are these? Are they quantitative? No, of course not because they have no measurements attached; they are qualitative observations.
What about other types of data that involve quantitative observations? Can we look at measurements and determine patterns? Yes we can. Statisticians, weather persons, stock market workers, sports analysts, and chemists (to name a few occupations) do this on a daily basis for their regular jobs. What if you were trying to identify an unknown substance based on a volume displacement experiment. You were given a series of known substances of known masses, and you then determined how much volume they displaced in a cylinder of water. Through your experiment, the following data was recorded (Table 3.6).
| Substance | Mass | Volume of Water Displaced |
|---|---|---|
| Aluminum | 3.7 g | 1.0 mL |
| Iron | 7.86 g | 1.0 mL |
| Copper | 8.92 g | 1.0 mL |
| Silver | 10.5 g | 1.0 mL |
| Zinc | 7.14 g | 1.0 mL |
| Lead | 11.34 g | 1.0 mL |
First, which metal do you think is the densest, just looking at the data table? Do you think it would be lead or aluminum? How can you tell? Lead is the right answer because there is a heavier mass of lead displacing the same volume of water. Did you notice that copper is heavier than iron, and iron is heavier than zinc? Now what kind of data do you think this is? Is it qualitative or quantitative? Quantitative is the right answer because we are dealing with measurements.
An interesting note is that 19.3 g of gold would have displaced the same volume of water. Would it be the densest? Yes it would. It also means that this same amount of gold converts to approximately 212.5 lb/gal. Remember seeing in television or movies where the villain is running off with a bag full of gold bars? This would be rather difficult knowing the density of the metal from this table. Being able to read tables and data gives us the power to understand the world around us.
Another way to generalize trends in data and to make interpretations based on these trends is to plot a graph. Graphs are like numerical pictures that provide an image of the data collected in an experiment. Suppose you were asked to record the temperature of a mixture as it was slowly heated in a hot water bath. You record the following data as you watch your experiment (Table 3.7). You then plot the data on a graph to see what the numbers tell you.
|
 |
Looking at the graph, what do you notice about the temperature of the mixture as it is heated in the hot water bath? It is constantly increasing. What does the initial point, or the y−intercept represent? It is the value of the initial temperature, most likely room temperature. Using a graph, it is clear to see that the y−axis, in this case temperature, is dependent on the x−axis. For our example, the independent variable is time. What does this mean? It means that for a change to be made in temperature, time must pass.
Being able to plot tables of values and read the corresponding graphs is an important skill, not only for mathematics but also for science. Interpretations can be made by using either of these representations; one may be more visual and thus sometimes easier to interpret than the other. Now try one example where you have to plot a graph and make some interpretations.
Making Calculations With Data
[edit | edit source]Being able to recognize patterns from tables, charts, pictures, and graphs is a worthy skill for any scientist and science student. By having charts, pictures, tables, and graphs, you can also perform a large variety of calculations depending on the independent and dependent variables. From here we can accomplish such things as making further predictions, drawing more conclusions, or identifying unknowns. Let’'s say, for example, in the density experiment from earlier, we were given an unknown for our experiment. Now, take the same chart but add a fourth column representing the density of the metal (Table 3.8). Recall the formula for density:
Now, filling in the fourth column, using the density formula for our experimental data, we see the following information. Remember density = mass/volume or, in the table below, column 4 = column 2 ÷ column 3.
| Substance | Mass | Volume of Water Displaced | Density |
|---|---|---|---|
| Aluminum | 3.7 g | 1.0 mL | 2.7 g/mL |
| Iron | 7.86 g | 1.0 mL | 7.86 g/mL |
| Copper | 8.92 g | 1.0 mL | 8.92 g/mL |
| Silver | 10.5 g | 1.0 mL | 10.5 g/mL |
| Zinc | 7.14 g | 1.0 mL | 7.14 g/mL |
| Lead | 11.34 g | 1.0 mL | 11.34 g/mL |
| Unknown | 1.78 g | 0.2 mL | 8.9 g/mL |
Just by doing this calculation, we can identify our unknown in the experiment? Sure, it is copper. Calculations are frequent in chemistry, as you will learn. Most times you will see we will use a variety of formulae to solve problems similar to those you would solve in any course. The relationship from comparing sets of answers give us the interesting parts of these types of calculations.
|
Sample Question How long does it take you to run 3.5 miles at 7 mph? Solution We know that:
Therefore:
|
Another important skill with calculations is converting from one unit to another. Frequently in chemistry, data will appear in problems that require us to use conversion factors before completing the problem. Some conversion factors include 100 cm = 1 m, 1000 mL = 1 L, and 1 km = 1000 m.
|
Sample Question The speed of light is 3.00×108 m/s. The speed of sound is 1230 km/h. How much faster is the speed of light than the speed of sound. Solution:
In other words, the speed of light is almost 900, 000 times faster than the speed of sound. Amazing isn't it! |
Preparing Graphs From Data
[edit | edit source]Most times in the laboratory, we collect data of some sort and then carry it back to our desk to analyze. We want to determine the melting point of an unknown solid, so we take the melting points of various knowns and then that of our unknown; following this, we make a table, finally writing the data gathered from our experiment into the table. Some laboratory experiments that we, as scientists, do require us to draw graphs in order to interpret the results and make any conclusions. Drawing a graph that anyone can understand is a useful skill to any scientist. Graphs have to be properly labeled on the x-axis (the horizontal) and the y-axis (the vertical). The graphs should indicate a straight line or smooth curve indicating that the data is continuous. A straight line represents a linear relationship; a curved line does not.
|
Sample Question Medical practitioners have been studying the heart for a long time. As a result, we can now calculate your heart rate based on a formula derived from your age. Plot the table of values given below. Properly label the graph to include the independent and dependent variable. Draw the line all the way to the y-axis so that you can find the y-intercept. Finally, find your age on the x-axis and then find your maximum heart rate by drawing a vertical line up to the graph.
Solution: At the age of 17, the maximum heart rate (beats per minute) read from the graph is 103.  |
Reading Results From the Graph
[edit | edit source]Many properties in chemistry lead to linear relationships when plotted. We saw this with the temperature/time relationship. Other properties in chemistry do not form this linear relationship. Take for example the relationship between concentration and temperature. Remember the last time you made a cup of instant coffee or hot chocolate? Why did you boil the water? What would have happened if you used warm tap water or even cold water from the refrigerator? Putting aside the anticipated taste difference, what would have happened to the solid you were trying to dissolve? The amount of instant coffee or hot chocolate powder in your cup that actually dissolves in warm or cold water would be small compared to when you use boiling water. This property is known as solubility. The solubility of a substance is the amount that can dissolve in a given amount of solution. Solubility is affected by the temperature but rarely linearly. Look at the data table below (Table 3.9). This data is for the solubility of KClO3 (potassium chlorate) in water.
| Temperature (°C) | Solubility (g/100 mL H2O |
|---|---|
| 0 | 3.3 |
| 20 | 7.3 |
| 40 | 13.9 |
| 60 | 23.8 |
| 80 | 37.5 |
| 100 | 56.3 |
Now graph the data and see what kind of curve we get.
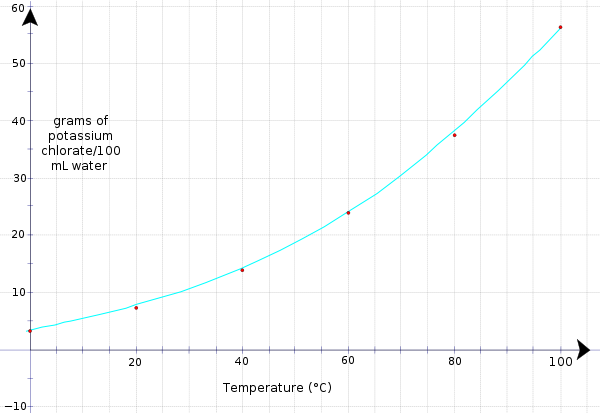
Notice how when the line is drawn, the relationship between grams of potassium chlorate that dissolve in 100 mL of water and temperature is not linear but curved. We can still interpret the data as we did earlier. For example, what is the solubility of KClO3 (how much KClO3) when the temperature is 75 °C or at room temperature.
Using the same procedure, we draw a line up from 75 °C and then over to the y−axis. It reads 34.5 g/100 mL. Therefore, 34.5 g of KClO3 can dissolve in 100 mL of H2O at 75 °C.

Now you try one:
|
Sample Question Ammonia, NH3, and sodium chloride, NaCl, are known to have the following solubility data (Table 3.10).
a) Properly graph the data for each substance. b) Are either of these linear? Explain. c) What would be the solubility of each of the substances at 50 °C? Solution: a) b) The Solubility data for NaCl represents a linear relationship when graphed. You can see this with the blue line in the graph above. The NH3 line (in red) is curved; therefore it is non-linear. c) The solubility of NH3 at 50 °C is 27 g/100 mL H2O. The solubility for NaCl at 50 °C is 37.5 g/100 mL H2O. The graph below is marked to show the line traveling up from 50 °C and over to the y-axis (solubility) to find the answer for both of these parts.  |
We can do more than just graph and read graphs of linear and non-linear data in order to make conclusions. For this, we use formulas like the slope of a line. Remember slope from math class? It is a formula used to find the rate at which one factor is affecting the other, either positively or negatively. Remember the formula for slope from math class?

Let's look at how the slope formula can be used on a graph to see how one factor is affecting another in an experiment.
In the 1800s, the use of the hot air balloons was extremely popular as a sport as well as an extracurricular activity for those who could afford the luxury. Up to this point, the study of the relationship of gases and the factors of temperature, pressure, and volume was limited to Robert Boyle's experiments with pressure and volume. Jacques Charles came along with his experiments on the relationship between volume and temperature. Here is some typical data from a volume/temperature experiment with gases (Table 3.11).
| Temperature (°C) | Volume of Gas (cm3) |
|---|---|
| 20 | 60 |
| 40 | 65 |
| 60 | 70 |
| 80 | 75 |
| 100 | 80 |
| 120 | 85 |

Now, find out what affect the temperature has on the volume of the gas. In other words, find the slope. Pick two points that are on the line and use the equation above to find the value of m.
What does this mean? It means that for each increase in temperature of 1 °C, the volume increased by 0.25 cm3 (or 0.25 mL). This translates to approximately 1 mL increase every 4 °C. This is a positive increase (notice the slope is increasing or going up). Now let's try another one.
Look at Table 3.12 for a set of data from an experiment performed between bromine and formic acid in a laboratory setting. The reaction was performed to see if the decrease in bromine concentration could cause the reaction to subsequently slow down. In other words, if they took some of the bromine out of the reaction, would the reaction start to slow down? Look at the data and see what happened.
| Reading | Concentration of Bromine (mol/L) |
Time |
|---|---|---|
| 1 | 0.1 | 0 |
| 2 | 0.07 | 0.75 |
| 3 | 0.05 | 1.75 |
| 4 | 0.035 | 2.49 |
| 5 | 0.02 | 3.48 |
| 6 | 0.01 | 5 |
| 7 | 0.005 | 6.2 |
| 8 | 0.001 | 7.5 |
| 9 | 0.0 | 8.8 |
| 10 | 00 | 9 |
Look at the data table, can you tell if an increase in bromine concentration had an effect on the rate of a reaction? Did it make it go faster or slower. Let's take a look. From T1 to T7 the bromine concentration decreased from 0.1 mol/L to 0.005 mol/L, a decrease of 0.095 mol/L. The time it took for this decrease was 6.2 seconds. What does this tell us about the rate? A preliminary conclusion would be that a decrease in bromine concentration causes the rate of the reaction to also decrease. A graph might make it a little easier to make conclusions based on the data.

Using slope to calculate the effect here is not as easy because we have a curve. We can easily see that as the concentration increases, so does the rate, but by how much? The slope would actually tell us that. In order to determine the slope of a curve, you need to draw in a tangent to the curve. A tangent is just a straight line drawn to the curve; from this you would calculate the slope. Look at the graph below, the tangents are drawn in using a red pen.

If we draw a tangent, look, we have a straight line. We can now find two points.
This means that as the concentration of bromine decreases, so does the rate of the reaction. Look at the units for the slope. The units are mol/L · s. These are the units for rate. This means, interestingly enough, that as the concentration goes down, the reaction slows down.
Lesson Summary
[edit | edit source]- Patterns can be found in data sets, pictures, charts, and graphs. From here scientists can make interpretations of the data and draw conclusions.
- When drawing graphs of tables of values, a straight line or a smooth curves can be drawn. Some data sets do require a line of best fit.
- A line of best fit is drawn on a scatter plot so that it joins as many points as possible and shows the general direction of the data. When constructing the line of best fit, it is also important to keep, approximately, an equal number of points above and below the line.
- Conversion factors are necessary for calculations where the units do not match. For example, km and m.
- Recall the slope formula:
- For curved lines, remember to draw the tangent first and then find the slope of the tangent line.
Review Questions
[edit | edit source]- Why is the slope of a graph so important to chemistry?
- What would you do to find the slope of a curved line?
- What is a conversion factor used for?
- Of the following professions, choose the one that uses data to find the identity of unknown fingerprints?
- (a) analytical chemist
- (b) archaeological chemist
- (c) inorganic scientist
- (d) forensic scientist
- (e) quality control chemist
- Which speed is the slowest?
- (a) 200 m/min (200 m/min × 1 km/1000 m = 0.2 km/min)
- (b) 0.2 km/min
- (c) 10 km/h (10 km/h × 1 h/6 min = 0.17 km/min)
- (d) 1.0×105 mm/min (1.0×105 mm/min × 1 m/1000 mm × 1 km/1000 m = 0.1 km/min)
- (e) 10 mi/h (10 mi/h × 1.603 km/mi × 1h/60 min = 0.267 km/min or 0.27 km/min)
- Andrew was completing his density lab for his chemistry lab exam. He collected the following data in his data table (Table 3.13).
Table 3.13 Mass of Solid (g) Volume of Solution (mL) 3.4 0.3 6.8 0.6 10.2 0.9 21.55 1.9 32.89 2.9 44.23 3.9 55.57 4.9 - (a) Draw a graph to represent the data.
- (b) Calculate the slope.
- (c) What does the slope of the line represent?
- (d) Can you help Andrew determine what his unknown is by looking in a standards table?
- Donna is completing the last step in her experiment to find the effect of the concentration of ammonia on the reaction. She has collected the following data from her time trials and is ready for the analysis (Table 3.14). Donna is now required to graph the data, describe the relationship, find the slope and then discuss the meaning of the slope. Help Donna with the interpretation of her data.
Table 3.14 Time (s) Concentration (mol/L) 0.20 49.92 0.40 39.80 0.60 29.67 0.81 20.43 1.08 14.39 1.30 10.84 1.53 5.86 2.00 1.95 2.21 1.07 2.40 0.71 2.60 0.71
Vocabulary
[edit | edit source]- alkali metals
- Group 1 metals of the periodic table (H, Li, Na, K, Rb, Cs, Fr).
- alkaline earth metals
- Group 2 metals of the periodic table (Be, Mg, Ca, Sr, Ba, Ra).
- chemical reactivity
- An observation of the behavior of the element of compound based on its position in a reactivity (or activity) series.
- conversion factor
- A ratio used to convert one unit to another.
- dependent variable
- The variable that changes depending on another variable (y-axis variable).
- graphs
- Pictorial representation of patterns using a coordinate system (x − y axis).
- independent variable
- The variable that changes to cause another variable to change (x-axis variable).
- line of best fit
- A line drawn on a graph so that it joins as many points as possible and shows the general direction of the data. When constructing the line of best fit, it is also important to keep, approximately, an equal number of points above and below the line.
- linear relationship
- A relationship where the x-values change proportionally with the y-values leading to a straight line.
- non-linear relationship
- A relationship where the x-values do not change proportionally with the y-values leading to a curved line.
- slope
- A formula to find the rate at which one factor is affecting the other.
- solubility
- The amount of a substance that can dissolve in a given amount of solution.
- tangent
- A straight line drawn to the curve.
- y-intercept
- Where the line crosses the y-axis.
This material was adapted from the original CK-12 book that can be found here. This work is licensed under the Creative Commons Attribution-Share Alike 3.0 United States License