Geometry for Elementary School/Congruence
In this chapter, we will start the discussion of congruence and congruence theorems. We say the two figures are congruent if they have the same shape and size. Congruent figures have three things in common: corresponding sides (corr. sides), corresponding angles (corr. ∠s) and corresponding points (corr. points). We will only talk about congruent triangles.
Congruent triangles
[edit | edit source]The triangles and are congruent if and only if all the following conditions hold:
- The side equals . (Corresponding sides)

- The side equals . (Corresponding sides)
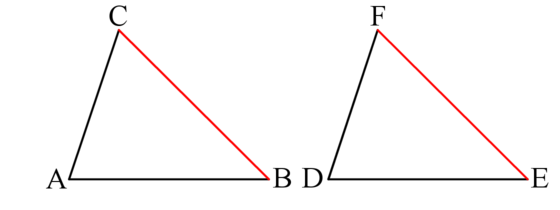
- The side equals . (Corresponding sides)

- The angle equals . (Corresponding angles)
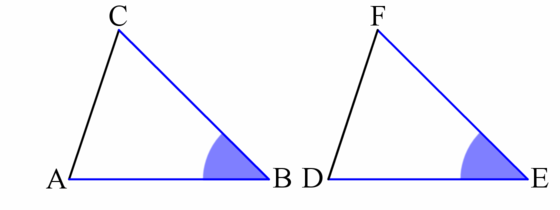
- The angle equals . (Corresponding angles)
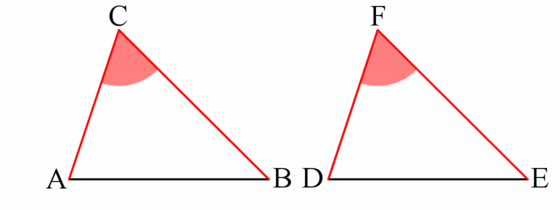
- The angle equals . (Corresponding angles)

Note that the order of vertices is important. It is possible that and are not congruent even though both refer to the same triangle. Remember that the place where corresponding points are must be the same on both triangles.
Congruence theorems give a set of the fewest conditions that are sufficient in order to show that two triangles are congruent. They are SSS, SAS, ASA, AAS and RHS. We will talk about them later on.
Finding the value of unknowns in triangles whose congruence is given
[edit | edit source]Let's say we have two triangles, and , and they are congruent. AB=3, ∠F=90° and ∠E=60°. We need to find DE and ∠A. Here's how:






















