Geometry Course/Polygon/Triangle/Right Triangle
Right Triangle
[edit | edit source]Right Triangle is a triangle that has one angle equal to 90o and the sum of the other two angles equal to 90o
Pythagoras's Theorem
[edit | edit source]The three sides of the right triangle relate to each other as shown
- (Hypotenuse)2 = (Adjacent)2 + (Opposite)2
Trigonometry Triangle
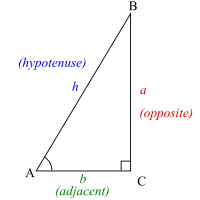
[edit | edit source]In right triangles, the trigonometric ratios of sine, cosine and tangent can be used to find unknown angles and the lengths of unknown sides. The sides of the triangle are known as follows:
- The hypotenuse is the side opposite the right angle, or defined as the longest side of a right-angled triangle, in this case h.
- The opposite side is the side opposite to the angle we are interested in, in this case a.
- The adjacent side is the side that is in contact with the angle we are interested in and the right angle, hence its name. In this case the adjacent side is b.
Sine
[edit | edit source]The sine of an angle is the ratio of the length of the opposite side to the length of the hypotenuse. In our case
Cosine
[edit | edit source]The cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse. In our case
Tangent
[edit | edit source]The tangent of an angle is the ratio of the length of the opposite side to the length of the adjacent side. In our case
The sine, cosine and tangent rules
[edit | edit source]
The law of sines, or sine rule,[1] states that the ratio of the length of a side to the sine of its corresponding opposite angle is constant, that is
This ratio is equal to the diameter of the circumscribed circle of the given triangle. Another interpretation of this theorem is that every triangle with angles , and is similar to a triangle with side lengths equal to , and . This triangle can be constructed by first constructing a circle of diameter 1, and inscribing in it two of the angles of the triangle. The length of the sides of that triangle will be , and . The side whose length is is opposite to the angle whose measure is , etc.
The law of cosines, or cosine rule, connects the length of an unknown side of a triangle to the length of the other sides and the angle opposite to the unknown side. As per the law:
For a triangle with length of sides , , and angles of , , respectively, given two known lengths of a triangle and , and the angle between the two known sides (or the angle opposite to the unknown side ), to calculate the third side , the following formula can be used:
If the lengths of all three sides of any triangle are known the three angles can be calculated:
The law of tangents or tangent rule, is less known than the other two. It states that:
It is not used very often, but can be used to find a side or an angle when you know two sides and an angle or two angles and a side.
- ↑ Prof. David E. Joyce. "The Laws of Cosines and Sines". Clark University. Retrieved 2008-11-01.





















![{\displaystyle {\frac {a-b}{a+b}}={\frac {\tan[{\frac {1}{2}}(\alpha -\beta )]}{\tan[{\frac {1}{2}}(\alpha +\beta )]}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b7a4a3592aa66976f1d34bbbb403daa392f9fdf)