GLSL Programming/Unity/Soft Shadows of Spheres

This tutorial covers soft shadows of spheres.
It is one of several tutorials about lighting that go beyond the Phong reflection model, which is a local illumination model and therefore doesn't take shadows into account. The presented technique renders the soft shadow of a single sphere on any mesh and is somewhat related to a technique that was proposed by Orion Sky Lawlor (see the “Further Reading” section). The shader can be extended to render the shadows of a small number of spheres at the cost of rendering performance; however, it cannot easily be applied to any other kind of shadow caster. Potential applications are computer ball games (where the ball is often the only object that requires a soft shadow and the only object that should cast a dynamic shadow on all other objects), computer games with a spherical main character (e.g. “Marble Madness”), visualizations that consist only of spheres (e.g. planetary visualizations, ball models of small nuclei, atoms, or molecules, etc.), or test scenes that can be populated with spheres and benefit from soft shadows.
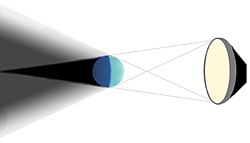

Soft Shadows
[edit | edit source]While directional light sources and point light sources produce hard shadows, any area light source generates a soft shadow. This is also true for all real light sources, in particular the sun and any light bulb or lamp. From some points behind the shadow caster, no part of the light source is visible and the shadow is uniformly dark: this is the umbra. From other points, more or less of the light source is visible and the shadow is therefore less or more complete: this is the penumbra. Finally, there are points from where the whole area of the light source is visible: these points are outside of the shadow.
In many cases, the softness of a shadow depends mainly on the distance between the shadow caster and the shadow receiver: the larger the distance, the softer the shadow. This is a well known effect in art; see for example the painting by Caravaggio to the right.

Computation
[edit | edit source]We are going to approximately compute the shadow of a point on a surface when a sphere of radius at S (relative to the surface point) is occluding a spherical light source of radius at L (again relative to the surface point); see the figure to the left.
To this end, we consider a tangent in direction T to the sphere and passing through the surface point. Furthermore, this tangent is chosen to be in the plane spanned by L and S, i.e. parallel to the view plane of the figure to the left. The crucial observation is that the minimum distance of the center of the light source and this tangent line is directly related to the amount of shadowing of the surface point because it determines how large the area of the light source is that is visible from the surface point. More precisely spoken, we require a signed distance (positive if the tangent is on the same side of L as the sphere, negative otherwise) to determine whether the surface point is in the umbra (), in the penumbra (), or outside of the shadow ().
For the computation of , we consider the angles between L and S and between T and S. The difference between these two angles is the angle between L and T, which is related to by:
.
Thus, so far we have:
We can compute the angle between T and S using
.
Thus:
.
For the angle between L and S we use a feature of the cross product:
.
Therefore:
.
All in all we have:
The approximation we did so far, doesn't matter much; more importantly it doesn't produce rendering artifacts. If performance is an issue one could go further and use arcsin(x) ≈ x; i.e., one could use:
This avoids all trigonometric functions; however, it does introduce rendering artifacts (in particular if a specular highlight is in the penumbra that is facing the light source). Whether these rendering artifacts are worth the gains in performance has to be decided for each case.
Next we look at how to compute the level of shadowing based on . As decreases from to , should increase from 0 to 1. In other words, we want a smooth step from 0 to 1 between values -1 and 1 of . Probably the most efficient way to achieve this is to use the Hermite interpolation offered by the built-in GLSL function smoothstep(a,b,x) = t*t*(3-2*t) with t=clamp((x-a)/(b-a),0,1):
While this isn't a particular good approximation of a physically-based relation between and , it still gets the essential features right.
Furthermore, should be 0 if the light direction L is in the opposite direction of S; i.e., if their dot product is negative. This condition turns out to be a bit tricky since it leads to a noticeable discontinuity on the plane where L and S are orthogonal. To soften this discontinuity, we can again use smoothstep to compute an improved value :
Additionally, we have to set to 0 if a point light source is closer to the surface point than the occluding sphere. This is also somewhat tricky because the spherical light source can intersect the shadow-casting sphere. One solution that avoids too obvious artifacts (but fails to deal with the full intersection problem) is:
In the case of a directional light source we just set . Then the term , which specifies the level of unshadowed lighting, should be multiplied to any illumination by the light source. (Thus, ambient light shouldn't be multiplied with this factor.) If the shadows of multiple shadow casters are computed, the terms for all shadow casters have to be combined for each light source. The common way is to multiply them although this can be inaccurate (in particular if the umbras overlap).
Implementation
[edit | edit source]The implementation computes the length of the lightDirection and sphereDirection vectors and then proceeds with the normalized vectors. This way, the lengths of these vectors have to be computed only once and we even avoid some divisions because we can use normalized vectors. Here is the crucial part of the fragment shader:
// computation of level of shadowing w
vec3 sphereDirection = vec3(_SpherePosition - position);
float sphereDistance = length(sphereDirection);
sphereDirection = sphereDirection / sphereDistance;
float d = lightDistance
* (asin(min(1.0,
length(cross(lightDirection, sphereDirection))))
- asin(min(1.0, _SphereRadius / sphereDistance)));
float w = smoothstep(-1.0, 1.0, -d / _LightSourceRadius);
w = w * smoothstep(0.0, 0.2,
dot(lightDirection, sphereDirection));
if (0.0 != _WorldSpaceLightPos0.w) // point light source?
{
w = w * smoothstep(0.0, _SphereRadius,
lightDistance - sphereDistance);
}
The use of asin(min(1.0, ...)) makes sure that the argument of asin is in the allowed range.
Complete Shader Code
[edit | edit source]The complete source code defines properties for the shadow-casting sphere and the light source radius. All values are expected to be in world coordinates. For directional light sources, the light source radius should be given in radians (1 rad = 180° / π). The best way to set the position and radius of the shadow-casting sphere is a short script that should be attached to all shadow-receiving objects that use the shader, for example:
@script ExecuteInEditMode()
var occluder : GameObject;
function Update () {
if (null != occluder) {
renderer.sharedMaterial.SetVector("_SpherePosition",
occluder.transform.position);
renderer.sharedMaterial.SetFloat("_SphereRadius",
occluder.transform.localScale.x / 2.0);
}
}
This script has a public variable occluder that should be set to the shadow-casting sphere. Then it sets the properties _SpherePostion and _SphereRadius of the following shader (which should be attached to the same shadow-receiving object as the script).
Shader "GLSL shadow of sphere" {
Properties {
_Color ("Diffuse Material Color", Color) = (1,1,1,1)
_SpecColor ("Specular Material Color", Color) = (1,1,1,1)
_Shininess ("Shininess", Float) = 10
_SpherePosition ("Sphere Position", Vector) = (0,0,0,1)
_SphereRadius ("Sphere Radius", Float) = 1
_LightSourceRadius ("Light Source Radius", Float) = 0.005
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" }
// pass for ambient light and first light source
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
uniform vec4 _SpherePosition;
// center of shadow-casting sphere in world coordinates
uniform float _SphereRadius;
// radius of shadow-casting sphere
uniform float _LightSourceRadius;
// in radians for directional light sources
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float lightDistance;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
lightDistance = 1.0;
}
else // point or spot light
{
lightDirection = vec3(_WorldSpaceLightPos0 - position);
lightDistance = length(lightDirection);
attenuation = 1.0 / lightDistance; // linear attenuation
lightDirection = lightDirection / lightDistance;
}
// computation of level of shadowing w
vec3 sphereDirection = vec3(_SpherePosition - position);
float sphereDistance = length(sphereDirection);
sphereDirection = sphereDirection / sphereDistance;
float d = lightDistance
* (asin(min(1.0,
length(cross(lightDirection, sphereDirection))))
- asin(min(1.0, _SphereRadius / sphereDistance)));
float w = smoothstep(-1.0, 1.0, -d / _LightSourceRadius);
w = w * smoothstep(0.0, 0.2,
dot(lightDirection, sphereDirection));
if (0.0 != _WorldSpaceLightPos0.w) // point light source?
{
w = w * smoothstep(0.0, _SphereRadius,
lightDistance - sphereDistance);
}
vec3 ambientLighting =
vec3(gl_LightModel.ambient) * vec3(_Color);
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
gl_FragColor = vec4(ambientLighting
+ (1.0 - w) * (diffuseReflection + specularReflection),
1.0);
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources
Blend One One // additive blending
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
uniform vec4 _SpherePosition;
// center of shadow-casting sphere in world coordinates
uniform float _SphereRadius;
// radius of shadow-casting sphere
uniform float _LightSourceRadius;
// in radians for directional light sources
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float lightDistance;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
lightDistance = 1.0;
}
else // point or spot light
{
lightDirection = vec3(_WorldSpaceLightPos0 - position);
lightDistance = length(lightDirection);
attenuation = 1.0 / lightDistance; // linear attenuation
lightDirection = lightDirection / lightDistance;
}
// computation of level of shadowing w
vec3 sphereDirection = vec3(_SpherePosition - position);
float sphereDistance = length(sphereDirection);
sphereDirection = sphereDirection / sphereDistance;
float d = lightDistance
* (asin(min(1.0,
length(cross(lightDirection, sphereDirection))))
- asin(min(1.0, _SphereRadius / sphereDistance)));
float w = smoothstep(-1.0, 1.0, -d / _LightSourceRadius);
w = w * smoothstep(0.0, 0.2,
dot(lightDirection, sphereDirection));
if (0.0 != _WorldSpaceLightPos0.w) // point light source?
{
w = w * smoothstep(0.0, _SphereRadius,
lightDistance - sphereDistance);
}
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
gl_FragColor = vec4((1.0 - w) * (diffuseReflection
+ specularReflection), 1.0);
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Specular"
}
Summary
[edit | edit source]Congratulations! I hope you succeeded to render some nice soft shadows. We have looked at:
- What soft shadows are and what the penumbra and umbra is.
- How to compute soft shadows of spheres.
- How to implement the computation, including a script in JavaScript that sets some properties based on another
GameObject.
Further Reading
[edit | edit source]If you still want to know more
- about the rest of the shader code, you should read Section “Smooth Specular Highlights”.
- about computations of soft shadows, you should read a publication by Orion Sky Lawlor: “Interpolation-Friendly Soft Shadow Maps” in Proceedings of Computer Graphics and Virtual Reality ’06, pages 111–117. A preprint is available online.























