GLSL Programming/GLUT/Diffuse Reflection

The light reflection from the surface of the moon is (in a good approximation) only diffuse.

This tutorial covers per-vertex diffuse reflection.

It's the first in a series of tutorials about basic lighting in OpenGL 2.x. In this tutorial, we start with diffuse reflection from a single directional light source and then include point lights and spotlights. Further tutorials cover extensions of this, in particular specular reflection, per-pixel lighting, two-sided lighting, and multiple light sources.

When appropriate, we'll use the same conventions as in OpenGL 1.x, so that people upgrading their OpenGL knowledge will feel at ease.

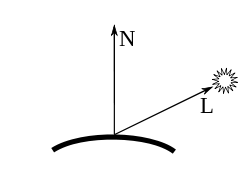
Diffuse reflection can be computed using the surface normal vector N and the light vector L, i.e. the vector to the light source.

Diffuse Reflection

The moon exhibits almost exclusively diffuse reflection (also called Lambertian reflection), i.e. light is reflected into all directions without specular highlights. Other examples of such materials are chalk and matte paper; in fact, any surface that appears dull and matte.

In the case of perfect diffuse reflection, the intensity of the observed reflected light depends on the cosine of the angle between the surface normal vector and the ray of the incoming light. As illustrated in the figure to the left, it is common to consider normalized vectors starting in the point of a surface, where the lighting should be computed: the normalized surface normal vector N is orthogonal to the surface and the normalized light direction L points to the light source.

For the observed diffuse reflected light $I_{\text{diffuse}}$, we need the cosine of the angle between the normalized surface normal vector N and the normalized direction to the light source L, which is the dot product N·L because the dot product a·b of any two vectors a and b is:

$\mathbf {a} \cdot \mathbf {b} =\left\vert \mathbf {a} \right\vert \left\vert \mathbf {b} \right\vert \cos \measuredangle (\mathbf {a} ,\mathbf {b} )$.

In the case of normalized vectors, the lengths |a| and |b| are both 1.

If the dot product N·L is negative, the light source is on the “wrong” side of the surface and we should set the reflection to 0. This can be achieved by using max(0, N·L), which makes sure that the value of the dot product is clamped to 0 for negative dot products. Furthermore, the reflected light depends on the intensity of the incoming light $I_{\text{incoming}}$ and a material constant $k_{\text{diffuse}}$ for the diffuse reflection: for a black surface, the material constant $k_{\text{diffuse}}$ is 0, for a white surface it is 1. The equation for the diffuse reflected intensity is then:

$I_{\text{diffuse}}=I_{\text{incoming}}\,k_{\text{diffuse}}\max(0,\mathbf {N} \cdot \mathbf {L} )$

For colored light, this equation applies to each color component (e.g. red, green, and blue). Thus, if the variables $I_{\text{diffuse}}$, $I_{\text{incoming}}$, and $k_{\text{diffuse}}$ denote color vectors and the multiplications are performed component-wise (which they are for vectors in GLSL), this equation also applies to colored light. This is what we actually use in the shader code.

Shader Code for One Directional Light Source

If we have only one directional light source, the shader code for implementing the equation for $I_{\text{diffuse}}$ is relatively small. In order to implement the equation, we follow the questions about implementing equations, which were discussed in the tutorial on silhouette enhancement:

• Should the equation be implemented in the vertex shader or the fragment shader? We try the vertex shader here. In the tutorial on smooth specular highlights, we will look at an implementation in the fragment shader.
• In which coordinate system should the equation be implemented? We chose world space, so that lights are described in the same coordinate system as positioned objects.
• Where do we get the parameters from? The answer to this is a bit longer:

As described in the tutorial on shading in view space, we make the diffuse material color $k_{\text{diffuse}}$ available as material.diffuse. The direction to the light source L in view space is available in light0.position (with the 4th vector element set to 0.0) and the light color $I_{\text{incoming}}$ is available as light0.diffuse. We get the surface normal vector in object coordinates from the attribute v_normal. Since we implement the equation in world space, we have to convert the surface normal vector from object space to world space as discussed in the tutorial on silhouette enhancement.

The vertex shader then looks like this:

attribute vec4 v_coord;
attribute vec3 v_normal;
uniform mat4 m, v, p;
uniform mat3 m_3x3_inv_transp;
varying vec4 color;

struct lightSource
{
  vec4 position;
  vec4 diffuse;
};
lightSource light0 = lightSource(
    vec4(-1.0, 1.0, -1.0, 0.0),
    vec4(1.0, 1.0, 1.0, 1.0)
);

struct material
{
  vec4 diffuse;
};
material mymaterial = material(vec4(1.0, 0.8, 0.8, 1.0));

void main(void)
{
  mat4 mvp = p*v*m;
  vec3 normalDirection = normalize(m_3x3_inv_transp * v_normal);
  vec3 lightDirection = normalize(vec3(light0.position));

  vec3 diffuseReflection
    = vec3(light0.diffuse) * vec3(mymaterial.diffuse)
    * max(0.0, dot(normalDirection, lightDirection));

  color = vec4(diffuseReflection, 1.0);
  gl_Position = mvp * v_coord;
}

And the fragment shader is:

varying vec4 color;

void main(void)
{
  gl_FragColor = color;
}

For now we only create one directional light source in the scene.

Changes for a Point Light Source

In the case of a directional light source light0.position specifies the direction from where light is coming. In the case of a point light source (or a spot light source), however, light0.position will specify the position of the light source in view space and we have to compute the direction to the light source as the difference vector from the position of the vertex in view space to the position of the light source. Since the 4th coordinate of a point is 1 and the 4th coordinate of a direction is 0, we can easily distinguish between the two cases:

  vec3 lightDirection;

  if (light0.position.w == 0.0) // directional light
    {
      lightDirection = normalize(vec3(light0.position));
    }
  else // point or spot light
    {
      lightDirection = normalize(vec3(light0.position - m * v_coord));
    }

While there is no attenuation of light for directional light sources, we should add some attenuation with distance to point and spot light source. As light spreads out from a point in three dimensions, it's covering ever larger virtual spheres at larger distances. Since the surface of these spheres increases quadratically with increasing radius and the total amount of light per sphere is the same, the amount of light per area decreases quadratically with increasing distance from the point light source. Thus, we should divide the intensity of the light source by the squared distance to the vertex.

We can specify a combination of quadratic attenuation with distance (rather rapid), linear attenuation with distance, and constant attenuation. The code would be:

struct lightSource
{
  vec4 position;
  vec4 diffuse;
  float constantAttenuation, linearAttenuation, quadraticAttenuation;
};
lightSource light0 = lightSource(
    vec4(-1.0, 1.0, -1.0, 1.0),
    vec4(1.0, 1.0, 1.0, 1.0),
    1.0, 0.0, 0.0
);

  vec3 lightDirection;
  float attenuation;

  if (light0.position.w == 0.0) // directional light
    {
      attenuation = 1.0; // no attenuation
      lightDirection = normalize(vec3(light0.position));
    }
  else // point or spot light
    { 
      vec3 vertexToLightSource = vec3(light0.position - m * v_coord);
      float distance = length(vertexToLightSource);
      attenuation = 1.0 / (light0.constantAttenuation 
                           + light0.linearAttenuation * distance
                           + light0.quadraticAttenuation * distance * distance);
      lightDirection = normalize(vertexToLightSource);
    }

The factor attenuation should then be multiplied with light0.diffuse to compute the incoming light; see the complete shader code below. Note that spot light sources have additional features, which are discussed in the next section.

Also note that this code is unlikely to give you the best performance because any if is usually quite costly. Since light0.position.w is either 0 or 1, it is actually not too hard to rewrite the code to avoid the use of if and optimize a bit further:

  vec3 vertexToLightSource = vec3(light0.position - m * v_coord * light0.position.w);
  float distance = length(vertexToLightSource);
  attenuation = mix(1.0,
                    1.0 / (light0.constantAttenuation 
                           + light0.linearAttenuation * distance
                           + light0.quadraticAttenuation * distance * distance),
                    gl_LightSource[0].position.w);
  lightDirection = vertexToLightSource / distance;

However, we will use the version with if for clarity. (“Keep it simple, stupid!”)

Changes for a Spotlight

The 0th light source is a spotlight only if light0.spotCutoff is less than or equal to 90.0 (otherwise we set it to 180.0). Thus, the test could be:

      if (light0.spotCutoff <= 90.0) // spotlight

The shape of a spotlight is described by the variable light0.spotDirection, light0.spotExponent and light0.spotCutoff. Specifically, if the cosine of the angle between -lightDirection and light0.spotDirection is smaller than the cosine of light0.spotCutoff, i.e. if the shaded point is outside the cone of light around the spotlight direction, then the attenuation factor is set to $0.0$. We can compute the cosine of the angle between the two vectors by a dot product of the two normalized vectors. (In OpenGL 1.x, the cosine of light0.spotCutoff was provided as gl_LightSource[0].spotCosCutoff.) If we include clamping of the cosine at 0 in order to ignore points behind the spotlight, the test is:

          float clampedCosine = max(0.0, dot(-lightDirection, normalize(light0.spotDirection)));
          if (clampedCosine < cos(light0.spotCutoff * 3.14159 / 180.0)) // outside of spotlight cone
            {
              attenuation = 0.0;
            }

Otherwise, if a point is inside the cone of light, the attenuation in OpenGL is supposed to be computed this way:

              attenuation = attenuation * pow(clampedCosine, light0.spotExponent);

This allows for wider (smaller spotExponent) and narrower (larger spotExponent) spotlights.

Complete Shader Code

All in all, our new vertex shader for a single directional light, point light, or spotlight with linear attenuation becomes:

attribute vec4 v_coord;
attribute vec3 v_normal;
uniform mat4 m, v, p;
uniform mat3 m_3x3_inv_transp;
varying vec4 color;

struct lightSource
{
  vec4 position;
  vec4 diffuse;
  float constantAttenuation, linearAttenuation, quadraticAttenuation;
  float spotCutoff, spotExponent;
  vec3 spotDirection;
};
lightSource light0 = lightSource(
    vec4(0.0,  1.0,  2.0, 1.0),
    vec4(1.0, 1.0, 1.0, 1.0),
    0.0, 1.0, 0.0,
    80.0, 20.0,
    vec3(-1.0, -0.5, -1.0)
);

struct material
{
  vec4 diffuse;
};
material mymaterial = material(vec4(1.0, 0.8, 0.8, 1.0));

void main(void)
{
  mat4 mvp = p*v*m;
  vec3 normalDirection = normalize(m_3x3_inv_transp * v_normal);
  vec3 lightDirection;
  float attenuation;

  if (light0.position.w == 0.0) // directional light
    {
      attenuation = 1.0; // no attenuation
      lightDirection = normalize(vec3(light0.position));
    }
  else // point or spot light (or other kind of light)
    {
      vec3 vertexToLightSource = vec3(light0.position - m * v_coord);
      float distance = length(vertexToLightSource);
      lightDirection = normalize(vertexToLightSource);
      attenuation = 1.0 / (light0.constantAttenuation
			   + light0.linearAttenuation * distance
			   + light0.quadraticAttenuation * distance * distance);

      if (light0.spotCutoff <= 90.0) // spotlight
	{
	  float clampedCosine = max(0.0, dot(-lightDirection, normalize(light0.spotDirection)));
	  if (clampedCosine < cos(light0.spotCutoff * 3.14159 / 180.0)) // outside of spotlight cone
	    {
	      attenuation = 0.0;
	    }
	  else
	    {
              attenuation = attenuation * pow(clampedCosine, light0.spotExponent);
	    }
	}
    }
  vec3 diffuseReflection = attenuation
    * vec3(light0.diffuse) * vec3(mymaterial.diffuse)
    * max(0.0, dot(normalDirection, lightDirection));

  color = vec4(diffuseReflection, 1.0);
  gl_Position = mvp * v_coord;
}

And the fragment shader is still:

varying vec4 color;

void main(void) {
  gl_FragColor = color;
}

In your C++ source code, make sure you update m_3x3_inv_transp:

  /* Transform normal vectors with transpose of inverse of upper left
     3x3 model matrix (ex-gl_NormalMatrix): */
  glm::mat3 m_3x3_inv_transp = glm::transpose(glm::inverse(glm::mat3(mesh.object2world)));
  glUniformMatrix3fv(uniform_m_3x3_inv_transp, 1, GL_FALSE, glm::value_ptr(m_3x3_inv_transp));

Summary

Congratulations! You already learned a lot about OpenGL lights. This is essential for the following tutorials about more advanced lighting. Specifically, we have seen:

• What diffuse reflection is and how to describe it mathematically.
• How to implement diffuse reflection for a single directional light source in a shader.
• How to extend the shader for point light sources with a linear attenuation.
• How to further extend the shader to handle spotlights.

Further Reading

If you still want to know more

• about transforming normal vectors into view space, you should read the tutorial on silhouette enhancement.
• about uniform variables provided by the compatibility profile, you should read the tutorial on Shading in View Space.

< GLSL Programming/GLUT

Unless stated otherwise, all example source code on this page is granted to the public domain.

Back to OpenGL Programming - Lighting section

Back to GLSL Programming - GLUT section