GCSE Computer Science/Sort Algorithms
Sort algorithms are a part of all GCSE Computer Science courses. Even when a course does not require knowing the name and definition of one or more of the sorting algorithms below, it is required to be able to understand and use these algorithms in a specific context.
Bubble Sort
[edit | edit source]|
Which Courses? AQA 3.1.4, Ed 1.1.8, OCR 2.1 |
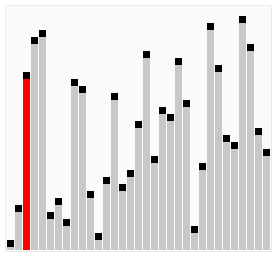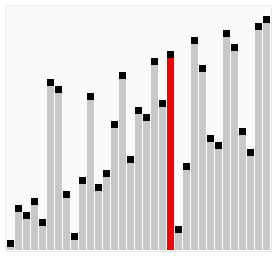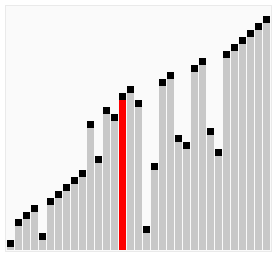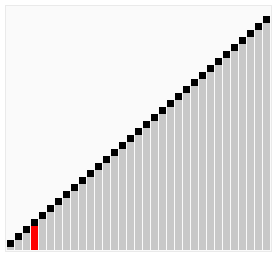
Bubble sort is a simple sorting algorithm that works by repeatedly stepping through the list to be sorted, comparing each pair and swapping them if they are in the wrong order. The pass through the list is repeated until no swaps are needed, which indicates that the list is sorted. The algorithm gets its name from the way larger elements "bubble" to the top of the list. It is a very slow way of sorting data and rarely used in industry. There are much faster sorting algorithms out there such as insertion sort which we will discuss next.

Step-by-step example
[edit | edit source]Let us take the array of numbers "5 1 4 2 8", and sort the array from lowest number to greatest number using bubble sort algorithm. In each step, elements written in bold are being compared.
First Pass:
( 5 1 4 2 8 ) ( 1 5 4 2 8 ), Here, algorithm compares the first two elements, and swaps them since 5 > 1
( 1 5 4 2 8 ) ( 1 4 5 2 8 ), It then compares the second and third items and swaps them since 5 > 4
( 1 4 5 2 8 ) ( 1 4 2 5 8 ), Swap since 5 > 2
( 1 4 2 5 8 ) ( 1 4 2 5 8 ), Now, since these elements are already in order (8 > 5), algorithm does not swap them.
The algorithm has reached the end of the list of numbers and the largest number, 8, has bubbled to the top. It now starts again.
Second Pass:
( 1 4 2 5 8 ) ( 1 4 2 5 8 ), no swap needed
( 1 4 2 5 8 ) ( 1 2 4 5 8 ), Swap since 4 > 2
( 1 2 4 5 8 ) ( 1 2 4 5 8 ), no swap needed
( 1 2 4 5 8 ) ( 1 2 4 5 8 ), no swap needed
Now, the array is already sorted, but our algorithm does not know if it is completed. The algorithm needs one whole pass without any swap to know it is sorted.
Third Pass:
( 1 2 4 5 8 ) ( 1 2 4 5 8 )
( 1 2 4 5 8 ) ( 1 2 4 5 8 )
( 1 2 4 5 8 ) ( 1 2 4 5 8 )
( 1 2 4 5 8 ) ( 1 2 4 5 8 )
Finally, the array is sorted, and the algorithm can terminate.
Exercises
[edit | edit source]1) Sort the following lists using a bubble sort. How many passes are needed?
(a) Sort into alphabetical order:
Henry, Cat, George, Mouse
Answer:
Cat, George, Henry, Mouse (Pass 1) Cat, George, Henry, Mouse (Pass 2) 2 passes
(b) Sort into alphabetical order:
G, C, N, A, P, CAnswer:
C, G, A, N, C, P (Pass 1) C, A, G, C, N, P (Pass 2) A, C, C, G, N, P (Pass 3) A, C, C, G, N, P (Pass 4) 4 passes
(c) Sort into numerical order:
12, 56, 0, 23, 10Answer:
12, 0, 23, 10, 56 (Pass 1) 0, 12, 10, 23, 56 (Pass 2) 0, 10, 12, 23, 56 (Pass 3) 0, 10, 12, 23, 56 (Pass 4) 4 passes
2) Show the following after 2 passes
(a) Sort into alphabetical order:
Emu, Shrike, Gull, Badger
Answer:
Emu, Gull, Badger, Shrike (Pass 1) Emu, Badger, Gull, Shrike (Pass 2)
(b) Sort into numerical order:
99, 45, 32, 56, 12
Answer:
45, 32, 56, 12, 99 (Pass 1) 32, 45, 12, 56, 99 (Pass 2)
Insertion Sort
[edit | edit source]|
Which Courses? AQA 3.1.4, Ed 1.1.8, OCR 2.1 |
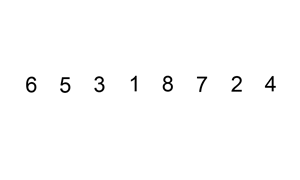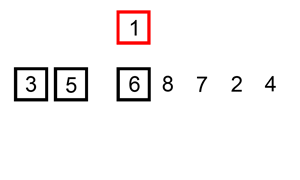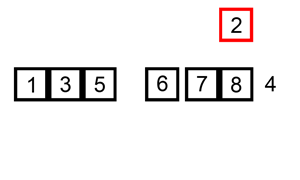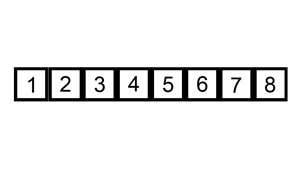
Unfortunately bubble sort is a very slow way of sorting data and very rarely used in industry. We'll now look at a much faster algorithm, insertion sort.
Insertion sort is a simple sorting algorithm: a comparison sort in which the sorted array (or list) is built one entry at a time. It is much less efficient on large lists than more advanced algorithms such as merge sort, which is covered below. However, insertion sort provides several advantages:
- simple implementation
- efficient on small data sets
- uses a fixed amount of memory when running
Insertion sort requires the use of two arrays, one ordered, and one unordered. Each repetition of the algorithm moves an item from the unordered list, into a sorted position in the ordered list, until there are no elements left in the unordered list.
Sorting is typically done in-place without needing extra memory. The resulting array after k iterations has the property where the first k + 1 entries are sorted. In each iteration the first remaining entry of the input is removed, inserted into the result at the correct position, thus extending the result:
becomes
with each element greater than x copied to the right as it is compared against x.
|
Example: Insertion Sort The following table shows the steps for sorting the sequence {5, 7, 0, 3, 4, 2, 6, 1}. For each iteration, the number of positions the inserted element has moved is shown in parentheses. Altogether this amounts to 17 steps. 5 7 0 3 4 2 6 1 (0)
0 5 7 3 4 2 6 1 (2) 0 3 5 7 4 2 6 1 (2) 0 3 4 5 7 2 6 1 (2) 0 2 3 4 5 7 6 1 (4) 0 2 3 4 5 6 7 1 (1) 0 1 2 3 4 5 6 7 (6) 5 7 0 3 4 2 6 1 (0)
0 5 7 3 4 2 6 1 (2) 0 3 5 7 4 2 6 1 (2) 0 3 4 5 7 2 6 1 (2) 0 2 3 4 5 7 6 1 (4) 0 2 3 4 5 6 7 1 (1) 0 1 2 3 4 5 6 7 (6)
|
|
Exercise: Insertion Sort Describe the process of insertion sort Answer:
Insertion sort is a simple sorting algorithm: a comparison sort in which the sorted array (or list) is built one entry at a time.
Show the how insert sort would work on the following unordered array: 9 6 7 1 2 Answer: sort left hand side is underlined 9 6 7 1 2 6 9 7 1 2 6 7 9 1 2 1 6 7 9 2 1 2 6 7 9 Show how the insert sort would work on the following unordered array G K L A J Answer: sort left hand side is underlined G K L A J G K L A J G K L A J A G K L J A G J K L |
Merge Sort
[edit | edit source]|
Which Courses? OCR 2.1 |




