Fundamentals of Transportation/Traffic Flow

Traffic Flow is the study of the movement of individual drivers and vehicles between two points and the interactions they make with one another. Unfortunately, studying traffic flow is difficult because driver behavior cannot be predicted with one-hundred percent certainty. Fortunately, drivers tend to behave within a reasonably consistent range; thus, traffic streams tend to have some reasonable consistency and can be roughly represented mathematically. To better represent traffic flow, relationships have been established between the three main characteristics: (1) flow, (2) density, and (3) velocity. These relationships help in planning, design, and operations of roadway facilities.
Traffic flow theory
[edit | edit source]
Time-Space Diagram
[edit | edit source]
Traffic engineers represent the location of a specific vehicle at a certain time with a time-space diagram. This two-dimensional diagram shows the trajectory of a vehicle through time as it moves from a specific origin to a specific destination. Multiple vehicles can be represented on a diagram and, thus, certain characteristics, such as flow at a certain site for a certain time, can be determined.
Flow and density
[edit | edit source]Flow (q) = the rate at which vehicles pass a fixed point (vehicles per hour) , = Average measured time headway
Density (Concentration) (k) = number of vehicles (N) over a stretch of roadway (L) (in units of vehicles per kilometer) [1]
where:
- = number of vehicles occupying a highway segment of length
- = equivalent hourly flow
- = length of roadway
- = density
Speed
[edit | edit source]Measuring speed of traffic is not as obvious as it may seem; we can average the measurement of the speeds of individual vehicles over time or over space, and each produces slightly different results.
Time mean speed
[edit | edit source]Time mean speed () = arithmetic mean of speeds of vehicles passing a point
Space mean speed
[edit | edit source]Space mean speed () is defined as the harmonic mean of speeds passing a point during a period of time. It also equals the average speeds over a length of roadway.
Relating time and space mean speed
[edit | edit source]Note that the time mean speed is average speed past a point as distinct from space mean speed which is average speed along a length.
The two speeds are related as
The time mean speed higher than the space mean speed, but the differences vary with the amount of variability within the speed of vehices. At high speeds (free flow), differences are minor, whereas in congested times, they might differ a factor 2.
Headway
[edit | edit source]The following definitions give what is referred to as the brutto gap (Asela) (Italian for gross), in contrast to netto gaps (Italian for net). Netto gaps give the distance or time between the rear bumper of a vehicle and the front bumper of the next.
Time headway
[edit | edit source]Time headway () = difference between the time when the front of a vehicle arrives at a point on the highway and the time the front of the next vehicle arrives at the same point (in seconds)
Average Time Headway () = Average Travel Time per Unit Distance * Average Space Headway
Space headway
[edit | edit source]Space headway () = difference in position between the front of a vehicle and the front of the next vehicle (in meters)
Average Space Headway ()= Space Mean Speed * Average Time Headway
Note that density and space headway are related:
Fundamental Diagram of Traffic Flow
[edit | edit source]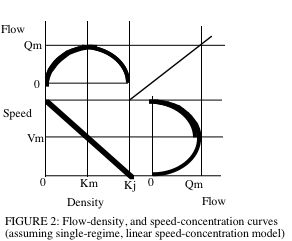

The variables of flow, density, and space mean speed are related definitionally as:
Traditional Model (Parabolic)
[edit | edit source]Properties of the traditional fundamental diagram.
- When density on the highway is zero, the flow is also zero because there are no vehicles on the highway
- As density increases, flow increases
- When the density reaches a maximum jam density (), flow must be zero because vehicles will line up end to end
- Flow will also increase to a maximum value (), increases in density beyond that point result in reductions of flow.
- Speed is space mean speed.
- At density = 0, speed is freeflow (). The upper half of the flow curve is uncongested, the lower half is congested.
- The slope of the flow density curve gives speed. Rise/Run = Flow/Density = Vehicles per hour/ Vehicles per km = km / hour.
Observation (Triangular or Truncated Triangular)
[edit | edit source]Actual traffic data is often much noisier than idealized models suggest. However, what we tend to see is that as density rises, speed is unchanged to a point (capacity) and then begins to drop if it is affected by downstream traffic (queue spillbacks). For a single link, the relationship between flow and density is thus more triangular than parabolic. When we aggregate multiple links together (e.g. a network), we see a more parabolic shape.
Microscopic and Macroscopic Models
[edit | edit source]Models describing traffic flow can be classed into two categories: microscopic and macroscopic. Ideally, macroscopic models are aggregates of the behavior seen in microscopic models.


Microscopic Models
[edit | edit source]Microscopic models predict the following behavior of cars (their change in speed and position) as a function of the behavior of the leading vehicle.
Macroscopic Models
[edit | edit source]Macroscopic traffic flow theory relates traffic flow, running speed, and density. Analogizing traffic to a stream, it has principally been developed for limited access roadways (Leutzbach 1988). The fundamental relationship “q=kv” (flow (q) equals density (k) multiplied by speed (v)) is illustrated by the fundamental diagram. Many empirical studies have quantified the component bivariate relationships (q vs. v, q vs. k, k vs. v), refining parameter estimates and functional forms (Gerlough and Huber 1975, Pensaud and Hurdle 1991; Ross 1991; Hall, Hurdle and Banks 1992; Banks 1992; Gilchrist and Hall 1992; Disbro and Frame 1992).
The most widely used model is the Greenshields model, which posited that the relationships between speed and density is linear. These were most appropriate before the advent of high-powered computers enabled the use of microscopic models. Macroscopic properties like flow and density are the product of individual (microscopic) decisions. Yet those microscopic decision-makers are affected by the environment around them, i.e. the macroscopic properties of traffic.
While traffic flow theorists represent traffic as if it were a fluid, queueing analysis essentially treats traffic as a set of discrete particles. These two representations are not-necessarily inconsistent. The figures to the right show the same 4 phases in the fundamental diagram and the queueing input-output diagram. This is discussed in more detail in the next section.
Examples
[edit | edit source]Example 1: Time-Mean and Space-Mean Speeds
[edit | edit source]
Given five observed velocities (50 km/hr, 35 km/hr, 45 km/hr, 20 km/hr, and 50 km/hr), what is the time-mean speed and space-mean speed?

Time-Mean Speed:
Space-Mean Speed:
The time-mean speed is 42 km/hr and the space-mean speed is 36.37 km/hr.
Example 2: Computing Traffic Flow Characteristics
[edit | edit source]
Given that 40 vehicles pass a given point in 1 minute and traverse a length of 1 kilometer, what is the flow, density, and time headway?

Compute flow and density:
Find space-mean speed:
Compute space headway:
Compute time headway:
The time headway is 1.5 seconds.
EXAMPLE 3: The spot speeds (expressed in km/hr) observed at a road section are 66, 62, 45, 79, 32, 51,56,60,53 and 49. The median speed (expressed in km/hr) is .
SOLUTION: Median speed is the speed at the middle value in series of spot speeds that are arranged in ascending order. 50% of speed values will be greater than the median 50% will be less than the median. Ascending order of spot speed studies are 32,39,45,51,53,56,60,62,66,79
Median speed = (53 +56 )/2=54.5 km/hr.
Thought Question
[edit | edit source]Problem
Microscopic traffic flow simulates the behaviors of individual vehicles while macroscopic traffic flow simulates the behaviors of the traffic stream overall. Conceptually, it would seem that microscopic traffic flow would be more accurate, as it would be based on driver behavior than simply flow characteristics. Assuming microscopic simulation could be calibrated to truly account for driver behaviors, what is the primary drawback to simulating a large network?
Solution
Computer power. To simulate a very large network with microscopic simulation, the number of vehicles that needed to be assessed is very large, requiring a lot of computer memory. Current computers have issues doing very large microscopic networks in a timely fashion, but perhaps future advances will do away with this issue.
Sample Problem
[edit | edit source]Variables
[edit | edit source]- = distance of nth vehicle
- = travel time of nth vehicle
- = speed (velocity) of nth vehicle
- = time headway between vehicles and
- = space (distance) headway between vehicles and
- = flow past a fixed point (vehicles per hour)
- = number of vehicles
- = time over which measurement takes place (number of seconds)
- = travel time
- = density (vehicles per km)
- = length of roadway section (km)
- = time mean speed
- = space mean speed
- = freeflow (uncongested speed)
- = jam density
- = maximum flow
Key Terms
[edit | edit source]- Time-space diagram
- Flow, speed, density
- Headway (space and time)
- Space mean speed, time mean speed
- Microscopic, Macroscopic
Supplementary Reading
[edit | edit source]Videos
[edit | edit source]References
[edit | edit source]- Banks, J.H. (1991). Two Capacity Phenomenon at Freeway Bottlenecks: A Basis for Ramp Metering? Transportation Research Record 1320, pp. 83–90.
- Banks, James H. (1992). “Freeway Speed-Flow-Concentration Relationships: More Evidence and Interpretations.” Transportation Research Record 1225:53-60.
- Cassidy, M.J. and R.L. Bertini (1999) Some Traffic Features at Freeway Bottlenecks. Transportation Research Part B Vol. 33, pp. 25–42
- Disbro, John E. and Frame, Michael. (1992). “Traffic Flow Theory and Chaotic Behavior.” Transportation Research Record. 1225: 109-115.
- Gerlough, Daniel L. and Huber, Matthew J. (1975). Traffic Flow Theory: A Monograph TRB Special Report 165. Transportation Research Board, Washington DC.
- Gilchrist, Robert S. and Fred L. Hall. (1992). “Three-Dimensional Relationships Among Traffic Flow Theory Variables.” Transportation Research Record. 1225:99-108.
- Hall, F.L. and K. Agyemang-Duah (1991). Freeway Capacity Drop and the Definition of Capacity. Transportation Research Record 1320, pp. 91–98
- Hall, Fred L., Hurdle, V. F., and Banks, James H. (1992). “A Synthesis of Recent Work on the Nature of Speed-Flow and Flow-Occupancy (or Density) Relationships on Freeways”. presented at TRB 71st Annual Meeting, Washington DC.
- Knoop, V.L., Hoogendoorn, S.P. and Van Zuylen, H.J. (2009) Empirical Differences between Time Mean Speed and Space Mean Speed. In Appert-Rolland, C., Chevoir, F., Gondret, P., Lassarre, S., Lebacque, J.-P. and Schreckenberg, M. (Eds.) Proceedings of Traffic and Granular Flow 07. pp. 351-356, Springer, New York
- Pensaud, B.N. and Hurdle, V. F. (1991). “Some New Data That Challenge Some Old Ideas About Speed-Flow Relationships.” Transportation Research Record. 1194: 191-8.
- Ross, Paul. (1991). “Some Properties of Macroscopic Traffic Models.” Transportation Research Record. 1194: 129-34.
End Notes
[edit | edit source]- ↑ Note: We use k because the word is Konzentration in German










































