Fundamentals of Physics/Motion in Two Dimensions
The Basics
[edit | edit source]The goal of this section is to understand how objects move in fully two dimensions. By contrast, one-dimensional motion concentrated on motion strictly along the or axis. Two dimensional motion is where an object undergoes motion along the and axes "at the same time." The position of an object in two-dimensional space can be plotted by its coordinate. These coordinates are found by the equations
and
.
Note that also evolving as an object moves are its speeds along two axes as well via
and
.
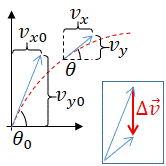
Remember that the and coordinates are perpendicular to each other, that is the and axes are orthogonal. This is a special relationship in math and physics, and means that processes along one axis do not affect processes along the other axis. Therefore, whatever happens along the axis does not affect what happens along the axis, and vice-versa. This is a key concept to understand. Two-dimensional motion is sometimes called "projectile motion" which encompasses objects flying through space under the influence of gravity. Baseballs, cannon balls, basketballs moving through space are all examples of projectile motion. Near the surface of the earth, projectiles in flight are restricted to motion where and m/s2. You can immediately find forms of the and equations above, given these restrictions. You can also find and equations, noting that will always be equal to a constant (vx0) since by orthogonality, g (gravity) only affects y and vy.
The Need for Vectors
[edit | edit source]At any given time, your object will have four quantities describing its motion: , , , and . Since position and velocity now each have two components (or parts), position and velocity will be "vectors," called and respectively. will consist of two components, the and coordinates of the object. Similarly, will consist of the components and . As you will now see, the two components of both and gives them both a magnitude (strength, length, etc.) and direction, which you must know how to handle.
Vectors: magnitude and angle
[edit | edit source]There are two ways of dealing with vectors, and you should be proficient with both. The first way is in "magnitude-angle form," where you report the magnitude of the vector and the angle at which it is pointing. For the position, the magnitude (or total distance from the origin) is . The angle this vector will make relative to the +x-axis is given by where . The absolute value signs are important to remove any negative values that might pop up and ensure the angle is with respect to the +x-axis. The velocity vector is tracked similarly, namely with , where is the angle the velocity vector makes with respect to the +x-axis, and is essentially the direction the object is moving in at that instant of time. Be sure you understand why a vector has a magnitude and an angle, and be sure you can always compute both from a given vector's components.
Vectors: Component form (or i,j,k notation)
[edit | edit source]Another way to express a vector is to use "component form." In this form, each component is listed directly next to a unit vector specifying what axis is associated with the component. If an object is meters along the x-axis and 2 m along the y-axis then , where and are unit vectors along the x-axis and y-axis, respectively. Likewise, if an object's velocity has an x-component of 3 m/s and a y-component of -2 m/s, its velocity vector would be . In some math textbooks an equivalent bracket notation is used: is equivalent to . In both notations, we say that the x component of is units and the ''y component is units (when doing the algebra with pencil and paper it is customary to omit units whenever the choice of units is obvious to the reader). These x and y components may be expressed using subscripts: and
Uniform Circular Motion
[edit | edit source]In the previous section we studied motion in two dimensions when the acceleration vector is a constant, which results in motion along a parabolic path. Another simple type of motion is uniform circular motion. Here, uniform refers to the fact that the speed remains constant (as the object moves in a circle). In this type of motion, the object always has an acceleration vector that points towards the center of the circle. If the circle's radius is and the speed, , is uniform, then the magnitude of the acceleration vector is . While the magnitude of the acceleration is uniform, the acceleration vector is not uniform because its direction is changing with respect to time. This acceleration is called "centripetal acceleration".


























![{\displaystyle {\vec {v}}=[3,-2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c34a1f427fd71ad300e01db11a0f423700ad61a)






