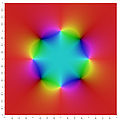
Fractals/Rational

Iteration of complex rational functions[1][2][3]
- analysis of rational map
- examples
Examples
[edit | edit source]- Newton fractals
- commons:Category:Complex rational maps
- The Boundedness Locus and baby Mandelbrot sets for some generalized McMullen maps by Suzanne Boyd, Alexander J. Mitchell 2023
- Mark McClure : a-julia-set-on-the-riemann-sphere
- f(z)=z2/(z9-z+0,025) [4]
- f(z)=(z3-z)/(dz2+1) where d=-0,003+0,995i [5]
- f(z)=(z3-z)/(dz2+1) where d=1,001· e2Pi/30 [6]
- Multibrot sets by Xender[7]
- [8]
- Rational Julia Sets by Marc McClure
- f(z) = (z^n+c)/(c^n+z), for n = -2 [9]
- Jasper Weinrich Burd: A Thompson-Like Group for the Bubble Bath Julia Set
- Abalone Fractals by Anders Sandberg, 2004
- (z2-1)/(z2+1). It has simple zeros at ±1 and simple poles at ±i.
- Shigehiro Ushiki = ComplexExplorer Page
- Rational maps with a superattracting 2-cycle by Wolf Jung
- Julia Sets of Cubic Rational Maps with Escaping Critical Points by Jun Hu, Arkady Etkin
- ON HYPERBOLIC RATIONAL MAPS WITH FINITELY CONNECTED FATOU SETS by YUSHENG LUO, 2021
- On geometrically finite degenerations I: boundaries of main hyperbolic components by Yusheng Luo, 2021
- On geometrically finite degenerations II: convergence and divergence by Yusheng Luo, 2021
- math.stackexchange question: how-to-compute-a-negative-multibrot-set
- Exotische Juliamengen - Jürgen Meier
- There are rational functions whose Julia set is the whole plane. The first example was given by Lattès: [10]
- Rational maps whose Julia sets are Cantor circles by Weiyuan Qiu, Fei Yang, Yongcheng Yin
- Petersen, C. L., and S. Zakeri. “On the Julia Set of a Typical Quadratic Polynomial with a Siegel Disk.” Annals of Mathematics, vol. 159, no. 1, 2004, pp. 1–52.
- A Note on a Quadratic Rational Map with Two Siegel Disks by Liang SHEN, Sheng Jian WU. Acta Mathematica Sinica, English Series. Jul., 2010, Vol. 26, No. 7, pp. 1393–1402 Published online: June 15, 2010 DOI: 10.1007/s10114-010-6611-3 Http://www.ActaMath.com
- MandelbrotMaps by Chris King
- fractalforums.org : z-plus-c2-z3-plus-c
Gallery
[edit | edit source]- Rational functions
-
-
-
-
-
-
- Rational functions
-
Blaschke fraction
[edit | edit source]
Analysis of critical points:
kill(all);
remvalue(all);
display2d:false;
ratprint : false; /* remove "rat :replaced " */
rho : -0.6170144002709304 +0.7869518599370003*%i;
define(f(z), rho * z^2 * (z-3)/(1-3*z));
/* first derivativa wrt z */
define( d(z), diff(f(z),z,1));
/* hipow does not expand expr, so hipow (expr, x) and hipow (expand (expr, x)) may yield different results */
n : hipow(num(expand(f(z))),z);
m : hipow(denom(expand(f(z))),z);
/* check if infinity is a fixed point */
limit(f(z),z,infinity);
/* finite critical points */
s:solve(d(z)=0)$
s : map(rhs,s)$
s : map('float,s)$
s : map('rectform,s)$
So there are 3 critical points :
- 2 finite critical points : z=1.0 i z= 0.0
- infinity
Dynamical plane consist of 3 basins
- basin of attraction of fixed point z = infinity ( superattracting) with inf many componnets
- basin of attraction of fixed point z = 0 ( superattracting) with inf many componnets
- basin of parabolic period 3 cycle ( with z= 1 critical point)
Finite Blaschke product
[edit | edit source]is a finite Blaschke product of degree n.[11] It is: [12]
- a rational function
- an analytic function on the open unit disc such that f can be extended to a continuous function on the closed unit disc that maps the unit circle to itself
- have no poles in the open unit disc
- In particular, if ƒ satisfies the condition above and has no zeros inside the unit circle, then ƒ is constant (this fact is also a consequence of the maximum principle for harmonic functions, applied to the harmonic function log(|ƒ(z)|)).
- the Blaschke products B are rational perturbations of the doubling map of the circle R(z) = z^2 (equivalently given by θ → 2θ (mod 1)).
- a finite Blaschke product may be uniquely described by the set of its critical points
- rational map which fix a disc = which takes the closed unit disc D to itself
- their iteration theory can be analyzed from the point of view of Fuchsian groups.
- polynomials’ in the hyperbolic plane = hyperbolic polynomial
- A finite Blaschke product, restricted to the unit circle, is a smooth covering map
- the unit disk D, the unit circle ∂D and the complement of the closed unit disk C\D are all completely invariant sets for B
where
- is a unimodular constant. It is a point which lies on the unit circle:
- is the multiplicity of the zero
- is a finite sequence of n points in the open unit disc
The building blocks[13] of Blaschke products are Mobius transformations of the form
where
- ak ∈ D := {z ∈ C|, |z| < 1}
- θk ∈ R.
A finite (infinite) Blaschke product has the form
Examples:
classification
[edit | edit source]There is a classification of finite Blaschke products in analogy with Möbius transformations.[14]
- B is elliptic if the Denjoy-Wolff point z0 of B lies in D. |B' (z0)| < 1.
- B is hyperbolic if the Denjoy-Wolff point z0 of B lies on ∂D and B'(z0) < 1,
- B is parabolic if the Denjoy-Wolff point z0 of B lies on ∂D and B'(z0) = 1,
The Denjoy-Wolff point of B is a unique z0 ∈ D such that for every z ∈ D
Julia set
[edit | edit source]Let B be a finite Blaschke product of degree d > 1. Julia set , the set on which the iterates fail to be normal on any neighbourhood is either the unit circle or a Cantor subset[15] [16]
- if B is elliptic, J(B) = ∂D,
- if B is hyperbolic, J(B) is a Cantor subset of D,
- if B is parabolic and z0 ∈ ∂D is the Denjoy-Wolff point of B,
- J(B) = ∂D if B(z0) = 0
- J(B) is a Cantor subset of ∂D if
- boudaries of BDM
critial orbit
[edit | edit source]McMullen maps
[edit | edit source]singularly perturbed maps, also called McMullen maps[17]
degree 2
[edit | edit source]-
reversed Basilica Julia set
Function:
maxima
Maxima 5.41.0 http://maxima.sourceforge.net
using Lisp GNU Common Lisp (GCL) GCL 2.6.12
Distributed under the GNU Public License. See the file COPYING.
Dedicated to the memory of William Schelter.
The function bug_report() provides bug reporting information.
(%i1) display2d:false;
(%o1) false
(%i2) f:z^2/(z^2-1);
(%o2) z^2/(z^2-1)
(%i3) dz:diff(f,z,1);
(%o3) (2*z)/(z^2-1)-(2*z^3)/(z^2-1)^2
(%i4) s:solve(f=z);
(%o4) [z = -(sqrt(5)-1)/2,z = (sqrt(5)+1)/2,z = 0]
(%i5) s:map('float,s);
(%o5) [z = -0.6180339887498949,z = 1.618033988749895,z = 0.0]
(%i6)
So fixed points :
- z = -0.6180339887498949
- z = 1.618033988749895
- z = 0.0
The Bubble bath Julia set
[edit | edit source]The quadratic rational function f:
The derivative wrt z is
The Julia set for f is called the Bubble Bath Julia set.[18] It is called the Bubble Bath for its visual similarity to a tub of bubbles.
Function f is defined for all z in the Riemann sphere = it is defined on the whole Riemann sphere
- The Fatou set of f is the basin of attraction of the 3-cycle consisting of the points 0, −1, and infinity. It is the only one attracting cycle and it is superattracting
- The Julia set J(f) is the set of points whose orbits are not attracted to the above 3-cycle
- the only critical points of f are:
- z = 0 because it is the pole of order 3 of d(z), the zero of 1/d(z)
- z = infinity because it is the zero of function d(z)
Maxima CAS code :
kill(all); remvalue(all); display2d:false; define(f(z), (1 -z^2)/(z^2)); (%o3) f(z):=(1-z^2)/z^2 define( d(z), ratsimp(diff(f(z),z,1))); (%o13) d(z):=-2/z^3 (%i14) limit(d(z),z,infinity); (%o14) 0 (%i15) limit(d(z),z,0); (%o15) infinity
(%i2) f(-1);
(%o2) 0
(%i3) limit(d(z),z,0);
(%o3) limit d(z)
z -> 0
(%i4) limit(f(z),z,0);
(%o4) inf
(%i5) limit(f(z),z,inf);
(%o5) - 1
Satbility of periodic cycle:
kill(all);
display2d:false;
ratprint : false; /* remove "rat :replaced " */
define(f(z), (1 -z^2)/(z^2));
F(z0):= block(
[z],
if is(z0 = 0) then z: limit(f(z),z,0)
elseif is(z0 = infinity) then z: limit(f(z),z,infinity)
elseif is(z0 = inf) then z: limit(f(z),z,inf)
else z:f(z0),
return(z)
)$
define( dz(z), ratsimp(diff(f(z),z,1)));
Dz(z0) := block(
[m,z],
if is(z0 = 0) then m: limit(dz(z),z,0)
elseif is(z0 = infinity) then m: limit(dz(z),z,infinity)
elseif is(z0 = inf) then m: limit(dz(z),z,inf)
else m:dz(z0),
return(m)
)$
GiveStability(z0, p):=block(
[z,d],
/* initial values */
d : 1,
z : z0,
for i:1 thru p step 1 do (
d : Dz(z)*d,
z: F(z)
/*print("i = ", 0, " d =",d, " z = ", z)*/
),
return (cabs(d))
)$
GiveStability(-1,3);
See also :
degree 2 by Michael Becker
[edit | edit source]1 period 4 basin
[edit | edit source]
degree 3
[edit | edit source]The components of the map contain the attracting points that are the solutions to . This is because the map is the one to use for finding solutions to the equation by Newton–Raphson formula. The solutions must naturally be attracting fixed points.
degree 3 by Michael Becker
[edit | edit source]1 period 2 basin
[edit | edit source]
2 critical points : { -0.4550898605622273*I -1.098684113467809, 0.4550898605622273*I+1.098684113467809}; Both critical points tend to the periodic cycle.
There is only one attractive period cycle : period 2 cycle = {0, infinity}.
Whole plane ( sphere) is a basin of attraction of period 2 cycle ( which is divided into 2 components ). Julia set is a boundary.
2 period 2 basins
[edit | edit source]-
only Julia set
-
Julia set, basins of attractions, critical orbits, attracting cycles
Function
where
- a = 2.099609375
- b = 0.349609375
Derivative:
d(z):=-(3*z^2+2.099609375)/(z^3+2.099609375*z+0.349609375)^2
Critical points:
[-0.8365822085525526*%i,0.8365822085525526*%i]
One can check it also using Wolfram Alpha
solve (3*z^2+2.099609375)/(z^3+2.099609375*z+0.349609375)^2=0
the result:
z = ± (5/16)* i* sqrt(43/6))
These are 2 finite critical points.
Infinity is a critical point too, as the 1st derivative's denominator degree is strictly greater than the numerator's. In numerical computations one can use the critical value (an image of critical point)
There are two period 2 cycle:
- { +0.4101296722285255 +0.5079485669960778*I , +0.4101296722285255 -0.5079485669960778*I };
- { +1.6890328811664648 +0.0000000000000000*I , +0.1147519899962205 +0.0000000000000000*I };
Both finite critical points fall into first cycle. Infinity ( or it's image zero) falls into the second cycle ( on the horizontal axis)
Infinity is not a fixed point
remvalue(all); display2d:false; define(f(z), 1/(z^3+ 2.099609375*z + 0.349609375)); (%i5)limit(f(z),z,infinity); (%o5) 0 (%i6) limit(f(z),z,0); (%o6) 2.860335195530726
degree 5
[edit | edit source]by L. Javier Hernandez Paricio
[edit | edit source]the rational map has six fixed points:
- ∞ ( repelling)
- −0,809017 − 0,587785i
- −0,809017 +0,587785i
- 0,309017 − 0,951057i
- 0,309017 + 0,951057i
- 1
the basin of an end point associated to a fixed point (6= ∞) of f is the same that the attraction basin of the Newton-Raphson numerical method when it is applied to find the roots of the equation [19]
degree 6
[edit | edit source]
The Julia set of the degree 6 function f :[20]
There are 3 superattracting fixed points at :
- z = 0
- z = 1
- z = ∞
All other critical points are in the backward orbit of 1.
How to compute iteration :
z:x+y*%i; z1:z^2*(3-z^4)/2; realpart(z1); ((x^2−y^2)*(−y^4+6*x^2*y^2−x^4+3)−2*x*y*(4*x*y^3−4*x^3*y))/2 imagpart(z1); (2*x*y*(−y^4+6*x^2*y^2−x^4+3)+(x^2−y^2)*(4*x*y^3−4*x^3*y))/2
Find fixed points using Maxima CAS :
z1:z^2*(3-z^4)/2; s:solve(z1=z); s:float(s);
result :
[z=−1.446857247913871,z=.7412709105660023,z=−1.357611535209976*%i−.1472068313260655,z=1.357611535209976*%i−.1472068313260655,z=1.0,z=0.0]
check multiplicities of the roots :
multiplicities; [1,1,1,1,1,1]
z1:z^2*(3-z^4)/2; s:solve(z1=z)$ s:map(rhs,s)$ f:z1; k:diff(f,z,1); define(d(z),k); m:map(d,s)$ m:map(abs,m)$ s:float(s); m:float(m);
Result : there are 6 fixed point 2 of them are supperattracting ( m=0 ), rest are repelling ( m>1 ):
[−1.446857247913871,.7412709105660023,−1.357611535209976*%i−.1472068313260655,1.357611535209976*%i−.1472068313260655,1.0,0.0] [14.68114348748323,1.552374536603988,10.66447061028112,10.66447061028112,0.0,0.0]
Critical points :
[%i,−1.0,−1.0*%i,1.0,0.0]
degree 9 by Michael Becker
[edit | edit source]
References
[edit | edit source]- Describing Blaschke products by their critical points by Oleg Ivrii, Tel Aviv University: video, presentation
- mathoverflow question: finding-the-critical-points-of-a-degree-5-blaschke-product
- ↑ Julia Sets of Complex. Polynomials and Their. Implementation on the Computer. by CM Stroh
- ↑ Julia sets by Michael Becker.
- ↑ DYNAMICS AND BIFURCATIONS OF A FAMILY OF RATIONAL MAPS WITH PARABOLIC FIXED POINTS by R. HAGIHARA AND J. HAWKINS
- ↑ f(z)=z2/(z9-z+0,025) by Esmeralda Rupp-Spangle
- ↑ f(z)=(z3-z)/(dz2+1) where d=-0,003+0,995i by Esmeralda Rupp-Spangle
- ↑ f(z)=(z3-z)/(dz2+1) where d=1,001· e2Pi/30 by Esmeralda Rupp-Spangle
- ↑ Rhapsody in Numbers by Xender
- ↑ Julia Sets for Rational Maps by PAUL BLANCHARD , CUZZOCREO, ROBERT L. DEVANEY, DANIEL M. LOOK, ELIZABETH D. RUSSELL
- ↑ fractalforums : Fractal Math, Chaos Theory & Research > General Discussion > Do z-->z/c² or z-->z*c² create a fractal
- ↑ math.stackexchange question: relation-between-filled-julia-set-and-julia-set-of-a-rational-function?
- ↑ Finite Blaschke products: a survey by Stephan Ramon Garcia, Javad Mashreghi, William T. Ross
- ↑ Dynamics of two-dimensional Blaschke products by ENRIQUE R. PUJALS and MICHAEL SHUB
- ↑ Color Visualization of Blaschke Product Mappings by Cristina Ballantine and Dorin Ghisa
- ↑ Epicycloids and Blaschke products by Chunlei Cao, Alastair Fletcher, Zhuan Ye
- ↑ THE EXPONENT OF CONVERGENCE OF A FINITE BLASCHKE PRODUCT by Gavin L. Jones. Annales Academiæ Scientiarum Fennicæ Mathematica Volumen 22, 1997, 245–254
- ↑ Blaschke products and parameter spaces by Katherine Plikuhn
- ↑ Symmetries for Julia sets of rational maps by Gustavo Rodrigues Ferreira
- ↑ A Thompson-Like Group for the Bubble Bath Julia Set by Jasper Weinrich-Burd, 2013
- ↑ Exterior discrete semiflows: Basins of end points by L. Javier Hernandez Paricio, Miguel Maranon Grandes ,M. Teresa Rivas Rodrıguez
- ↑ ON THURSTON’S PULLBACK MAP by XAVIER BUFF, ADAM EPSTEIN, SARAH KOCH, AND KEVIN PILGRIM
See also
[edit | edit source]- On the dynamics of rational maps by Mañé, R. ; Sad, P. ; Sullivan, D. Annales scientifiques de l'École Normale Supérieure, Série 4, Tome 16 (1983) no. 2, pp. 193-217.
- Rational maps: the structure of Julia sets from accessible Mandelbrot sets by Fitzgibbon, Elizabeth Laura
- Iteration of Rational Functions by Omar Antolín Camarena
- math.stackexchange question: attracting-or-parabolic-cycles-other-than-fixed-points
- 3D rational Julia sets by Algoristo