Formal Logic/Print version
| This is the print version of Formal Logic You won't see this message or any elements not part of the book's content when you print or preview this page. |
Sets
[edit | edit source]Presentations of logic vary in how much set theory they use. Some are heavily laden with set theory. Though most are not, it is nearly impossible to avoid it completely. It will not be a very important focal point for this book, but we will use a little set theory vocabulary here and there. This section introduces the vocabulary and notation used.
Sets and elements
[edit | edit source]Mathematicians use 'set' as an undefined primitive term. Some authors resort to quasi-synonyms such as 'collection'.
A set has elements. 'Element' is also undefined in set theory. We say that an element is a member of a set, also an undefined expression. The following are all used synonymously:
- x is a member of y
- x is contained in y
- x is included in y
- y contains x
- y includes x
Notation
[edit | edit source]A set can be specified by enclosing its members within curly braces.
is the set containing 1, 2, and 3 as members. The curly brace notation can be extended to specify a set using a rule for membership.
- (The set of all x such that x = 1 or x = 2 or x = 3)
is again the set containing 1, 2, and 3 as members.
- , and
both specify the set containing 1, 2, 3, and onwards.
A modified epsilon is used to denote set membership. Thus
indicates that "x is a member of y". We can also say that "x is not a member of y" in this way:
Characteristics of sets
[edit | edit source]A set is uniquely identified by its members. The expressions
all specify the same set even though the concept of an even prime is different from the concept of a positive square root. Repetition of members is inconsequential in specifying a set. The expressions
all specify the same set.
Sets are unordered. The expressions
all specify the same set.
Sets can have other sets as members. There is, for example, the set
Some special sets
[edit | edit source]As stated above, sets are defined by their members. Some sets, however, are given names to ease referencing them.
The set with no members is the empty set. The expressions
all specify the empty set. Empty sets can also express oxymora ("four-sided triangles" or "birds with radial symmetry") and factual non-existence ("the King of Czechoslovakia in 1994").
A set with exactly one member is called a singleton. A set with exactly two members is called a pair. Thus {1} is a singleton and {1, 2} is a pair.
ω is the set of natural numbers, {0, 1, 2, ...}.
Subsets, power sets, set operations
[edit | edit source]Subsets
[edit | edit source]A set s is a subset of set a if every member of s is a member of a. We use the horseshoe notation to indicate subsets. The expression
says that {1, 2} is a subset of {1, 2, 3}. The empty set is a subset of every set. Every set is a subset of itself. A proper subset of a is a subset of a that is not identical to a. The expression
says that {1, 2} is a proper subset of {1, 2, 3}.
Power sets
[edit | edit source]A power set of a set is the set of all its subsets. A script 'P' is used for the power set.
Union
[edit | edit source]The union of two sets a and b, written a ∪ b, is the set that contains all the members of a and all the members of b (and nothing else). That is,
As an example,
Intersection
[edit | edit source]The intersection of two sets a and b, written a ∩ b, is the set that contains everything that is a member of both a and b (and nothing else). That is,
As an example,
Relative complement
[edit | edit source]The relative complement of a in b, written b \ a (or b − a) is the set containing all the members of b that are not members of a. That is,
As an example,
Ordered sets, relations, and functions
[edit | edit source]The intuitive notions of ordered set, relation, and function will be used from time to time. For our purposes, the intuitive mathematical notion is the most important. However, these intuitive notions can be defined in terms of sets.
Ordered sets
[edit | edit source]First, we look at ordered sets. We said that sets are unordered:
But we can define ordered sets, starting with ordered pairs. The angle bracket notation is used for this:
Indeed,
Any set theoretic definition giving ⟨a, b⟩ this last property will work. The standard definition of the ordered pair ⟨a, b⟩ runs:
This means that we can use the latter notation when doing operations on an ordered pair.
There are also bigger ordered sets. The ordered triple ⟨a, b, c⟩ is the ordered pair ⟨⟨a, b⟩, c⟩. The ordered quadruple ⟨a, b, c, d⟩ is the ordered pair ⟨⟨a, b, c⟩, d⟩. This, in turn, is the ordered triple ⟨⟨⟨a, b⟩, c⟩, d⟩. In general, an ordered n-tuple ⟨a1, a2, ..., an⟩ where n greater than 1 is the ordered pair ⟨⟨a1, a2, ..., an-1⟩, an⟩.
It can be useful to define an ordered 1-tuple as well: ⟨a⟩ = a.
These definitions are somewhat arbitrary, but it is nonetheless convenient for an n-tuple, n ⟩ 2, to be an n-1 tuple and indeed an ordered pair. The important property that makes them serve as ordered sets is:
Relations
[edit | edit source]We now turn to relations. Intuitively, the following are relations:
- x < y
- x is a square root of y
- x is a brother of y
- x is between y and z
The first three are binary or 2-place relations; the fourth is a ternary or 3-place relation. In general, we talk about n-ary relations or n-place relations.
First consider binary relations. A binary relation is a set of ordered pairs. The less than relation would have among its members ⟨1, 2⟩, ⟨1, 3⟩, ⟨16, 127⟩, etc. Indeed, the less than relation defined on the natural numbers ω is:
Intuitively, ⟨x, y⟩ is a member of the less than relation if x < y. In set theory, we do not worry about whether a relation matches an intuitive concept such as less than. Rather, any set of ordered pairs is a binary relation.
We can also define a 3-place relation as a set of 3-tuples, a 4-place relation as a set of 4-tuples, etc. We only define n-place relations for n ≥ 2. An n-place relation is said to have an arity of n. The following example is a 3-place relation.
Because all n-tuples where n > 1 are also ordered pairs, all n-place relations are also binary relations.
Functions
[edit | edit source]Finally, we turn to functions. Intuitively, a function is an assignment of values to arguments such that each argument is assigned at most one value. Thus the + 2 function assigns a numerical argument x the value x + 2. Calling this function f, we say f(x) = x + 2. The following define specific functions.
Note that f3 is undefined when x = 0. According to biblical tradition, f4 is undefined when x = Adam or x = Eve. The following do not define functions.
Neither of these assigns unique values to arguments. For every positive x, there are two square roots, one positive and one negative, so f5 is not a function. For many x, x will have multiple sons, so f6 is not a function. If f6 is assigned the value the son of x then a unique value is implied by the rules of language, therefore f6 will be a function.
A function f is a binary relation where, if ⟨x, y⟩ and ⟨x, z⟩ are both members of f, then y = z.
We can define many place functions. Intuitively, the following are definitions of specific many place functions.
Thus ⟨4, 7, 11⟩ is a member of the 2-place function f7. ⟨3, 4, 5, 35⟩ is a member of the 3 place function f8
The fact that all n-tuples, n ≥ 2, are ordered pairs (and hence that all n-ary relations are binary relations) becomes convenient here. For n ≥ 1, an n-place function is an n+1 place relation that is a 1-place function. Thus, for a 2-place function f,
Goals
[edit | edit source]Sentential logic
[edit | edit source]Sentential logic attempts to capture certain logical features of natural languages. In particular, it covers truth-functional connections for sentences. Its formal language specifically recognizes the sentential connections
- It is not the case that _____
- _____ and _____
- Either _____ or _____
- _____ or _____ (or both)
- if _____, then _____
- _____ if and only if _____
The blanks are to be filled with statements that can be true or false. For example, "it is raining today" or "it will snow tomorrow". Whether the final sentence is true or false is entirely determined on whether the filled statements are true or false. For example, if it is raining today, but it will not snow tomorrow, then it is true to say that "Either it is raining today or it will snow tomorrow". On the other hand, it is false to say "it is raining today and it will snow tomorrow", since it won't snow tomorrow.
"Whether a statement is true or false" is called the truth value in logician slang. Thus "Either it is raining today or it is not raining today" has a truth value of true and "it is raining today and it is not raining today" has truth value of false.
Note that the above listed sentential connections do not include all possible truth value combinations. For example, there is no connection that is true when both sub-statements are true, both sub-statements are false or the first sub-statement is true while the other is false, and that is false else. However, you can combine the above connections together to build any truth combination of any number of sub-statements.
Issues
[edit | edit source]Already we have tacitly taken a position in ongoing controversy. Some questions already raised by the seemingly innocuous beginning above are listed.
- Should we admit into our logic only sentences that are true or false? Multi-valued logics admit a greater range of sentences.
- Are the connections listed above truly truth functional? Should we admit connections that are not truth functional sentences into our logic?
- What should logic take as its truth-bearers (objects that are true or false)? The two leading contenders today are sentences and propositions.
- Sentences. These consist of a string of words and perhaps punctuation. The sentence 'The cat is on the mat' consists of six elements: 'the', 'cat', 'is', 'on', another 'the', and 'mat'.
- Propositions. These are the meanings of sentences. They are what is expressed by a sentence or what someone says when he utters a sentence. The proposition that the cat is on the mat consists of three elements: a cat, a mat, and the on-ness relation.
- Elsewhere in Wikibooks and Wikipedia, you will see the name 'Propositional Logic' (or rather 'Propositional Calculus', see below) and the treatment of propositions much more often than you will see the name 'Sentential Logic' and the treatment of sentences. Our choice here represents the contributor's view as to which position is more popular among current logicians and what you are most likely to see in standard textbooks on the subject. Considerations as to whether the popular view is actually correct are not taken up here.
- Some authors will use talk about statements instead of sentences. Most (but not all) such authors you are likely to encounter take statements to be a subset of sentences, namely those sentences that are either true or false. This use of 'statement' does not represent a third position in the controversy, but rather places such authors in the sentences camp. (However, other—particularly older—uses of 'statement' may well place its authors in a third camp.)
Sometimes you will see 'calculus' rather than 'logic' such as in 'Sentential Calculus' or 'Propositional Calculus' as opposed to 'Sentential Logic' or 'Propositional Logic'. While the choice between 'sentential' and 'propositional' is substantive and philosophical, the choice between 'logic' and 'calculus' is merely stylistic.
The Sentential Language
[edit | edit source]This page informally describes our sentential language which we name . A more formal description will be given in Formal Syntax and Formal Semantics
Language components
[edit | edit source]Sentence letters
[edit | edit source]Sentences in are represented as sentence letters, which are single letters such as and so on. Some texts restrict these to lower case letters, and others restrict them to capital letters. We will use capital letters.
Intuitively, we can think of sentence letters as English sentences that are either true or false. Thus, may translate as 'The Earth is a planet' (which is true), or 'The moon is made of green cheese' (which is false). But may not translate as 'Great ideas sleep furiously' because such a sentence is neither true nor false. Translations between English and work best if they are restricted to timelessly true or false present tense sentences in the indicative mood. You will see in the translation section below that we do not always follow that advice, wherein we present sentences whose truth or falsity is not timeless.
Sentential connectives
[edit | edit source]Sentential connectives are special symbols in Sentential Logic that represent truth functional relations. They are used to build larger sentences from smaller sentences. The truth or falsity of the larger sentence can then be computed from the truth or falsity of the smaller ones.
- Translates to English as 'and'.
- is called a conjunction and and are its conjuncts.
- is true if both and are true—and is false otherwise.
- Some authors use an & (ampersand), • (heavy dot) or juxtaposition. In the last case, an author would write
- instead of our
- Translates to English as 'or'.
- is called a disjunction and and are its disjuncts.
- is true if at least one of and are true—is false otherwise.
- Some authors may use a vertical stroke: |. However, this comes from computer languages rather than logicians' usage. Logicians normally reserve the vertical stroke for nand (alternative denial). When used as nand, it is called the Sheffer stroke.
- Translates to English as 'it is not the case that' but is normally read 'not'.
- is called a negation.
- is true if is false—and is false otherwise.
- Some authors use ~ (tilde) or −. Some authors use an overline, for example writing
- instead of
- Translates to English as 'if...then' but is often read 'arrow'.
- is called a conditional. Its antecedent is and its consequent is .
- is false if is true and is false—and true otherwise.
- By that definition, is equivalent to
- Some authors use ⊃ (hook).
- Translates to English as 'if and only if'
- is called a biconditional.
- is true if and both are true or both are false—and false otherwise.
- By that definition, is equivalent to the more verbose . It is also equivalent to , the conjunction of two conditionals where in the second conditional the antecedent and consequent are reversed from the first.
- Some authors use ≡.
Grouping
[edit | edit source]Parentheses and are used for grouping. Thus
are two different and distinct sentences. Each negation, conjunction, disjunction, conditional, and biconditionals gets a single pair or parentheses.
Notes
[edit | edit source](1) An atomic sentence is a sentence consisting of just a single sentence letter. A molecular sentence is a sentence with at least one sentential connective. The main connective of a molecular formula is the connective that governs the entire sentence. Atomic sentences, of course, do not have a main connective.
(2) The ⊃ and ≡ signs for conditional and biconditional are historically older, perhaps a bit more traditional, and definitely occur more commonly in WikiBooks and Wikipedia than our arrow and double arrow. They originate with Alfred North Whitehead and Bertrand Russell in Principia Mathematica. Our arrow and double arrow appear to originate with Alfred Tarski, and may be a bit more popular today than the Whitehead and Russell's ⊃ and ≡.
(3) Sometimes you will see people reading our arrow as implies. This is fairly common in WikiBooks and Wikipedia. However, most logicians prefer to reserve 'implies' for metalinguistic use. They will say:
- If P then Q
or even
- P arrow Q
They approve of:
- 'P' implies 'Q'
but will frown on:
- P implies Q
Translation
[edit | edit source]Consider the following English sentences:
- If it is raining and Jones is out walking, then Jones has an umbrella.
- If it is Tuesday or it is Wednesday, then Jones is out walking.
To render these in , we first specify an appropriate English translation for some sentence letters.
- It is raining.
- Jones is out walking.
- Jones has an umbrella.
- It is Tuesday.
- It is Wednesday.
We can now partially translate our examples as:
Then finish the translation by adding the sentential connectives and parentheses:
Quoting convention
[edit | edit source]For English expressions, we follow the logical tradition of using single quotes. This allows us to use ' 'It is raining' ' as a quotation of 'It is raining'.
For expressions in , it is easier to treat them as self-quoting so that the quotation marks are implicit. Thus we say that the above example translates (note the lack of quotes) as 'If it is Tuesday, then It is raining'.
Formal Syntax
[edit | edit source]In The Sentential Language, we informally described our sentential language. Here we give its formal syntax or grammar. We will call our language .
Vocabulary
[edit | edit source]- Sentence letters: Capital letters 'A' – 'Z', each with (1) a superscript '0' and (2) a natural number subscript. (The natural numbers are the set of positive integers and zero.) Thus the sentence letters are:
- Sentential connectives:
- Grouping symbols:
The superscripts on sentence letters are not important until we get to the predicate logic, so we won't really worry about those here. The subscripts on sentence letters are to ensure an infinite supply of sentence letters. On the next page, we will abbreviate away most superscripts and subscripts.
Expressions
[edit | edit source]Any string of characters from the vocabulary is an expression of . Some expressions are grammatically correct. Some are as incorrect in as 'Over talks David Mary the' is in English. Still other expressions are as hopelessly ill-formed in as 'jmr.ovn asgj as;lnre' is in English.
We call a grammatically correct expression of a well-formed formula. When we get to Predicate Logic, we will find that only some well formed formulas are sentences. For now though, we consider every well formed formula to be a sentence.
Construction rules
[edit | edit source]An expression of is called a well-formed formula of if it is constructed according to the following rules.
- The expression consists of a single sentence letter
- The expression is constructed from other well-formed formulae and in one of the following ways:
In general, we will use 'formula' as shorthand for 'well-formed formula'. Since all formulae in are sentences, we will use 'formula' and 'sentence' interchangeably.
Quoting convention
[edit | edit source]We will take expressions of to be self-quoting and so regard
to include implicit quotation marks. However, something like
requires special consideration. It is not itself an expression of since and are not in the vocabulary of . Rather they are used as variables in English which range over expressions of . Such a variable is called a metavariable, and an expression using a mix of vocabulary from and metavariables is called a metalogical expression. Suppose we let be and be Then (1) becomes
- '' '' ''
which is not what we want. Instead we take (1) to mean (using explicit quotes):
- the expression consisting of '' followed by followed by '' followed by followed by '' .
Explicit quotes following this convention are called Quine quotes or corner quotes. Our corner quotes will be implicit.
Additional terminology
[edit | edit source]We introduce (or, in some cases, repeat) some useful syntactic terminology.
- We distinguish between an expression (or a formula) and an occurrence of an expression (or formula). The formula
is the same formula no matter how many times it is written. However, it contains three occurrences of the sentence letter and two occurrences of the sentential connective .
- is a subformula of if and only if and are both formulae and contains an occurrence of . is a proper subformula of if and only if (i) is a subformula of and (ii) is not the same formula as .
- An atomic formula or atomic sentence is one consisting solely of a sentence letter. Or put the other way around, it is a formula with no sentential connectives. A molecular formula or molecular sentence is one which contains at least one occurrence of a sentential connective.
- The main connective of a molecular formula is the last occurrence of a connective added when the formula was constructed according to the rules above.
- A negation is a formula of the form where is a formula.
- A conjunction is a formula of the form where and are both formulae. In this case, and are both conjuncts.
- A disjunction is a formula of the form where and are both formulae. In this case, and are both disjuncts.
- A conditional is a formula of the form where and are both formulae. In this case, is the antecedent, and is the consequent. The converse of is . The contrapositive of is .
- A biconditional is a formula of the form where and are both formulae.
Examples
[edit | edit source]By rule (i), all sentence letters, including
are formulae. By rule (ii-a), then, the negation
is also a formula. Then by rules (ii-c) and (ii-b), we get the disjunction and conjunction
as formulae. Applying rule (ii-a) again, we get the negation
as a formula. Finally, rule (ii-c) generates the conditional of (1), so it too is a formula.
This appears to be generated by rule (ii-c) from
The second of these is a formula by rule (i). But what about the first? It would have to be generated by rule (ii-b) from
But
cannot be generated by rule (ii-a). So (2) is not a formula.
Informal Conventions
[edit | edit source]In The Sentential Language, we gave an informal description of a sentential language, namely . We have also given a Formal Syntax for . Our official grammar generates a large number of parentheses. This makes formal definitions and other specifications easier to write, but it makes the language rather cumbersome to use. In addition, all the subscripts and superscripts quickly get to be unnecessarily tedious. The end result is an ugly and difficult to read language.
We will continue to use official grammar for specifying formalities. However, we will informally use a less cumbersome variant for other purposes. The transformation rules below convert official formulae of into our informal variant.
Transformation rules
[edit | edit source]We create informal variants of official formulae as follows. The examples are cumulative.
- The official grammar required sentence letters to have the superscript '0'. Superscripts aren't necessary or even useful until we get to the predicate logic, so we will always omit them in our informal variant. We will write, for example, instead of .
- We will omit the subscript if it is '0'. Thus we will write instead of . However, we cannot omit all subscripts; we still need to write, for example, .
- We will omit outermost parentheses. For example, we will write
- instead of
- We will let a series of the same binary connective associate on the right. For example, we can transform the official
- into the informal
- However, the best we can do with
- is
- We will use precedence rankings to omit internal parentheses when possible. For example, we will regard as having lower precedence (wider scope) than . This allows us to write
- instead of
- However, we cannot remove the internal parentheses from
- Our informal variant of this latter formula is
- Full precedence rankings are given below.
Precedence and scope
[edit | edit source]Precedence rankings indicate the order that we evaluate the sentential connectives. has a higher precedence than . Thus, in calculating the truth value of
we start by evaluating the truth value of
first. Scope is the length of expression that is governed by the connective. The occurrence of in (1) has a wider scope than the occurrence of . Thus the occurrence of in (1) governs the whole sentence while the occurrence of in (1) governs only the occurrence of (2) in (1).
The full ranking from highest precedence (narrowest scope) to lowest precedence (widest scope) is:
| highest precedence (narrowest scope) | |||
| lowest precedence (widest scope) |
Examples
[edit | edit source]Let's look at some examples. First,
can be written informally as
Second,
can be written informally as
Some unnecessary parentheses may prove helpful. In the two examples above, the informal variants may be easier to read as
and
Note that the informal formula
is restored to its official form as
By contrast, the informal formula
is restored to its official form as
Formal Semantics
[edit | edit source]English syntax for 'Dogs bark' specifies that it consists of a plural noun followed by an intransitive verb. English semantics for 'Dogs bark' specify its meaning, namely that dogs bark.
In The Sentential Language, we gave an informal description of . We also gave a Formal Syntax. However, at this point our language is just a toy, a collection of symbols we can string together like beads on a necklace. We do have rules for how those symbols are to be ordered. But at this point those might as well be aesthetic rules. The difference between well-formed formulae and ill-formed expressions is not yet any more significant than the difference between pretty and ugly necklaces. In order for our language to have any meaning, to be usable in saying things, we need a formal semantics.
Any given formal language can be paired with any of a number of competing semantic rule sets. The semantics we define here is the usual one for modern logic. However, alternative semantic rule-sets have been proposed. Alternative semantic rule-sets of have included (but are certainly not limited to) intuitionistic logics, relevance logics, non-monotonic logics, and multi-valued logics.
Formal semantics
[edit | edit source]The formal semantics for a formal language such as goes in two parts.
- Rules for specifying an interpretation. An interpretation assigns semantic values to the non-logical symbols of a formal syntax. The semantics for a formal language will specify what range of values can be assigned to which class of non-logical symbols. has only one class of non-logical symbols, so the rule here is particularly simple. An interpretation for a sentential language is a valuation, namely an assignment of truth values to sentence letters. In predicate logic, we will encounter interpretations that include other elements in addition to a valuation.
- Rules for assigning semantic values to larger expressions of the language. For sentential logic, these rules assign a truth value to larger formulae based on truth values assigned to smaller formulae. For more complex syntaxes (such as for predicate logic), values are assigned in a more complex fashion.
An extended valuation assigns truth values to the molecular formulae of (or similar sentential language) based on a valuation. A valuation for sentence letters is extended by a set of rules to cover all formulae.
Valuations
[edit | edit source]We can give a (partial) valuation as:
(Remember that we are abbreviating our sentence letters by omitting superscripts.)
Usually, we are only interested in the truth values of a few sentence letters. The truth values assigned to other sentence letters can be random.
Given this valuation, we say:
Indeed, we can define a valuation as a function taking sentence letters as its arguments and truth values as its values (hence the name 'truth value'). Note that does not have a fixed interpretation or valuation for sentence letters. Rather, we specify interpretations for temporary use.
Extended valuations
[edit | edit source]An extended interpretation generates the truth values of longer sentences given an interpretation. For sentential logic, an interpretation is a valuation, so an extended interpretation is an extended valuation. We define an extension of valuation as follows.
For all sentence letters and from
Example
[edit | edit source]We will determine the truth value of this example sentence given two valuations.
First, consider the following valuation:
(2) By clause (i):
(3) By (1) and clause (iii),
(4) By (1) and clause (iv),
(5) By (4) and clause (v),
(6) By (3), (5) and clause (v),
Thus (1) is false in our interpretation.
Next, try the valuation:
(7) By clause (i):
(8) By (7) and clause (iii),
(9) By (7) and clause (iv),
(10) By (9) and clause (v),
(11) By (8), (10) and clause (v),
Thus (1) is true in this second interpretation. Note that we did a bit more work this time than necessary. By clause (v), (8) is sufficient for the truth of (1).
Truth Tables
[edit | edit source]In the Formal Syntax, we earlier gave a formal semantics for sentential logic. A truth table is a device for using this form syntax in calculating the truth value of a larger formula given an interpretation (an assignment of truth values to sentence letters). Truth tables may also help clarify the material from the Formal Syntax.
Basic tables
[edit | edit source]Negation
[edit | edit source]We begin with the truth table for negation. It corresponds to clause (ii) of our definition for extended valuations.
|
T and F represent True and False respectively. Each row represents an interpretation. The first column shows what truth value the interpretation assigns to the sentence letter . In the first row, the interpretation assigns the value True. In the second row, the interpretation assigns the value False.
The second column shows the value receives under a given row's interpretation. Under the interpretation of the first row, has the value False. Under the interpretation of the second row, has the value True.
We can put this more formally. The first row of the truth table above shows that when = True, = False. The second row shows that when = False, = True. We can also put things more simply: a negation has the opposite truth value than that which is negated.
Conjunction
[edit | edit source]The truth table for conjunction corresponds to clause (iii) of our definition for extended valuations.
|
Here we have two sentence letters and so four possible interpretations, each represented by a single row. The first two columns show what the four interpretations assign to and . The interpretation represented by the first row assigns both sentence letters the value True, and so on. The last column shows the value assigned to . You can see that the conjunction is true when both conjuncts are true—and the conjunction is false otherwise, namely when at least one conjunct is false.
Disjunction
[edit | edit source]The truth table for disjunction corresponds to clause (iv) of our definition for extended valuations.
|
Here we see that a disjunction is true when at least one of the disjuncts is true—and the disjunction is false otherwise, namely when both disjuncts are false.
Conditional
[edit | edit source]The truth table for conditional corresponds to clause (v) of our definition for extended valuations.
|
A conditional is true when either its antecedent is false or its consequent is true (or both). It is false otherwise, namely when the antecedent is true and the consequent is false.
Biconditional
[edit | edit source]The truth table for biconditional corresponds to clause (vi) of our definition for extended valuations.
|
A biconditional is true when both parts have the same truth value. It is false when the two parts have opposite truth values.
Example
[edit | edit source]We will use the same example sentence from Formal Semantics:
We construct its truth table as follows:
|
With three sentence letters, we need eight valuations (and so lines of the truth table) to cover all cases. The table builds the example sentence in parts. The column was based on the and columns. The column was based on the and columns. This in turn was the basis for its negation in the next column. Finally, the last column was based on the and columns.
We see from this truth table that the example sentence is false when both and are true, and it is true otherwise.
This table can be written in a more compressed format as follows.
|
The numbers above the connectives are not part of the truth table but rather show what order the columns were filled in.
Satisfaction and validity of formulae
[edit | edit source]Satisfaction
[edit | edit source]In sentential logic, an interpretation under which a formula is true is said to satisfy that formula. In predicate logic, the notion of satisfaction is a bit more complex. A formula is satisfiable if and only if it is true under at least one interpretation (that is, if and only if at least one interpretation satisfies the formula). The example truth table of Truth Tables showed that the following sentence is satisfiable.
For a simpler example, the formula is satisfiable because it is true under any interpretation that assigns the value True.
We use the notation to say that the interpretation satisfies . If does not satisfy then we write
The concept of satisfaction is also extended to sets of formulae. A set of formulae is satisfiable if and only if there is an interpretation under which every formula of the set is true (that is, the interpretation satisfies every formula of the set).
A formula is unsatisfiable if and only if there is no interpretation under which it is true. A trivial example is
You can easily confirm by doing a truth table that the formula is false no matter what truth value an interpretation assigns to . We say that an unsatisfiable formula is logically false. One can say that an unsatisfiable formula of sentential logic (but not one of predicate logic) is tautologically false.
Validity
[edit | edit source]A formula is valid if and only if it is satisfied under every interpretation. For example,
is valid. You can easily confirm by a truth table that it is true no matter what the interpretation assigns to . We say that a valid sentence is logically true. We call a valid formula of sentential logic—but not one of predicate logic—a tautology.
We use the notation to say that is valid and to indicate is not valid.
Equivalence
[edit | edit source]Two formulae are equivalent if and only if they are true under exactly the same interpretations. You can easily confirm by truth table that any interpretation that satisfies also satisfies . In addition, any interpretation that satisfies also satisfies . Thus they are equivalent.
We can use the following convenient notation to say that and are equivalent.
which is true if and only if
Validity of arguments
[edit | edit source]An argument is a set of formulae designated as premises together with a single sentence designated as the conclusion. Intuitively, we want the premises jointly to constitute a reason to believe the conclusion. For our purposes an argument is any set of premises together with any conclusion. That can be a bit artificial for some particularly silly arguments, but the logical properties of an argument do not depend on whether it is silly or whether anyone actually does or might consider the premises to be a reason to believe the conclusion. We consider arguments as if one does or might consider the premises to be a reason for the conclusion independently of whether anyone actually does or might do so. Even an empty set of premises together with a conclusion counts as an argument.
The following example show the same argument using several notations.
- Notation 1
- Therefore
- Notation 2
- ∴
- Notation 3
- Notation 4
- ∴
An argument is valid if and only if every interpretation that satisfies all the premises also satisfies the conclusion. A conclusion of a valid argument is a logical consequence of its premises. We can express the validity (or invalidity) of the argument with as its set of premises and as its conclusion using the following notation.
- (1)
- (2)
For example, we have
Validity for arguments, or logical consequence, is the central notion driving the intuitions on which we build a logic. We want to know whether our arguments are good arguments, that is, whether they represent good reasoning. We want to know whether the premises of an argument constitute good reason to believe the conclusion. Validity is one essential feature of a good argument. It is not the only essential feature. A valid argument with at least one false premise is useless. Validity is the truth-preserving feature. It does not tell us that the conclusion is true, only that the logical features of the argument are such that, if the premises are true, then the conclusion is. A valid argument with true premises is sound.
There are other less formal features that a good argument needs. Just because the premises are true does not mean that they are believed, that we have any reason to believe them, or that we could collect evidence for them. It should also be noted that validity only applies to certain types of arguments, particularly deductive arguments. Deductive arguments are intended to be valid. The archetypical example for a deductive argument is a mathematical proof. Inductive arguments, of which scientific arguments provide the archetypical example, are not intended to be valid. The truth of the premises are not intended to guarantee that the conclusion is true. Rather, the truth of the premises are intended to make the truth of the conclusion highly probably or likely. In science, we do not intend to offer mathematical proofs. Rather, we gather evidence.
Formulae and arguments
[edit | edit source]For every valid formula, there is a corresponding valid argument having the valid formula as its conclusion and the empty set as its set of premises. Thus
if and only if
For every valid argument with finitely many premises, there is a corresponding valid formula. Consider a valid argument with as the conclusion and having as its premises . Then
There is then the corresponding valid formula
There corresponds to the valid argument
- ∴
the following valid formula:
Implication
[edit | edit source]You may see some text reading our arrow as 'implies' and using 'implications' as an alternative for 'conditional'. This is generally decried as a use-mention error. In ordinary English, the following are considered grammatically correct:
- (3) 'That there is smoke implies that there is fire'.
- (4) 'There is smoke' implies 'there is fire'.
In (3), we have one fact or proposition or whatever (the current favorite among philosophers appears to be proposition) implying another of the same species. In (4), we have one sentence implying another.
But the following is considered incorrect:
- There is smoke implies there is fire.
Here, in contrast to (3), there are no quotation marks. Nothing is the subject doing the implying and nothing is the object implied. Rather, we are composing a larger sentence out of smaller ones as if 'implies' were a grammatical conjunction such as 'only if'.
Thus logicians tend to avoid using 'implication' to mean conditional. Rather, they use 'implies' to mean has as a logical consequence and 'implication' to mean valid argument. In doing this, they are following the model of (4) rather than (3). In particular, they read (1) and (2) as ' implies (or does not imply) .
Expressibility
[edit | edit source]Formula truth tables
[edit | edit source]A formula with n sentence letters requires lines in its truth table. And, for a truth table of m lines, there are possible formulas. Thus, for a sentence of n letters, and the number of possible formulas is .
For example, there are four possible formulas of one sentence letter (requiring a two-line truth table) and 16 possible formulas of two sentence letters (requiring a four-line truth table). We illustrate this with the following tables. The numbered columns represent the different possibilities for the column of a main connective.
|
Column (iii) is the negation formula presented earlier.
|
Column (ii) represents the formula for disjunction, column (v) represents conditional, column (vii) represents biconditional, and column (viii) represents conjunction.
Expressing arbitrary formulas
[edit | edit source]The question arises whether we have enough connectives to represent all the formulas of any number of sentence letters. Remember that each row represents one valuation. We can express that valuation by conjoining sentence letters assigned True under that valuation and negations of sentence letters assigned false under that valuation. The four valuations of the second table above can be expressed as
Now we can express an arbitrary formula by disjoining the valuations under which the formula has the value true. For example, we can express column (x) with:
- (1)
You can confirm by completing the truth table that this produces the desired result. The formula is true when either (a) is true and is false or (b) is false and is true. There is an easier way to express this same formula: . Coming up with a simple way to express an arbitrary formula may require insight, but at least we have an automatic mechanism for finding some way to express it.
Now consider a second example. We want to express a formula of , , and , and we want this to be true under (and only under) the following three valuations.
| (i) | (ii) | (iii) | |||||
| True | False | False | |||||
| True | True | False | |||||
| False | False | True |
We can express the three conditions which yield true as
Now we need to say that either the first condition holds or that the second condition holds or that the third condition holds:
- (2)
You can verify by a truth table that it yields the desired result, that the formula is true in just the interpretation above.
This technique for expressing arbitrary formulas does not work for formulas evaluating to False in every interpretation. We need at least one interpretation yielding True in order to get the formula started. However, we can use any tautologically false formula to express such formulas. will suffice.
Normal forms
[edit | edit source]A normal form provides a standardized rule of expression where any formula is equivalent to one which conforms to the rule. It will be useful in the following to define a literal as a sentence letter or its negation (e.g. , and as well as , and ).
Disjunctive normal form
[edit | edit source]We say a formula is in disjunctive normal form if it is a disjunction of conjunctions of literals. An example is . For the purpose of this definition we admit so called degenerate disjunctions and conjunctions of only one disjunct or conjunct. Thus we count as being in disjunctive normal form because it is a degenerate (one-place) disjunction of a degenerate (one-place) conjunction. The degeneracy can be removed by converting it to the equivalent formula . We also admit many-place disjunctions and conjunctions for the purposes of this definition, such as . A method for finding the disjunctive normal form of a arbitrary formula is shown above.
Conjunctive normal form
[edit | edit source]There is another common normal form in sentential logic, namely conjunctive normal form. A formula is in conjunctive normal form if it is a conjunction of disjunctions of literals. An example is . Again, we can express arbitrary formulas in conjunctive normal form. First, take the valuations for which the formula evaluates to False. For each such valuation, form a disjunction of sentence letters the valuation assigns False together with the negations of sentence letters the valuation assign true. For the valuation
- : False
- : True
- : False
we form the disjunction
The conjunctive normal form expression of an arbitrary formula is the conjunction of all such disjunctions matching the interpretations for which the formula evaluates to false. The conjunctive normal form equivalent of (1) above is
The conjunctive normal form equivalent of (2) above is
Interdefinability of connectives
[edit | edit source]Negation and conjunction are sufficient to express the other three connectives and indeed any arbitrary formula.
Negation and disjunction are sufficient to express the other three connectives and indeed any arbitrary formula.
Negation and conditional are sufficient to express the other three connectives and indeed any arbitrary formula.
Negation and biconditional are not sufficient to express the other three connectives.
Joint and alternative denials
[edit | edit source]We have seen that three pairs of connectives are each jointly sufficient to express any arbitrary formula. The question arises, is it possible to express any arbitrary formula with just one connective? The answer is yes, but not with any of our connectives. There are two possible binary connectives each of which, if added to , would be sufficient.
Alternative denial
[edit | edit source]Alternative denial, sometimes called NAND. The usual symbol for this is called the Sheffer stroke, written as (some authors use ↑). Temporarily add the symbol to and let be True when at least one of or is false. It has the truth table :
|
We now have the following equivalences.
Joint denial
[edit | edit source]Joint denial, sometimes called NOR. Temporarily add the symbol to and let be True when both and are false. It has the truth table :
|
We now have the following equivalences.
Properties of Sentential Connectives
[edit | edit source]Here we list some of the more famous, historically important, or otherwise useful equivalences and tautologies. They can be added to the ones listed in Interdefinability of connectives. We can go on at quite some length here, but will try to keep the list somewhat restrained. Remember that for every equivalence of and , there is a related tautology .
Bivalence
[edit | edit source]Every formula has exactly one of two truth values.
- Law of Excluded Middle
- Law of Non-Contradiction
Analogues to arithmetic laws
[edit | edit source]Some familiar laws from arithmetic have analogues in sentential logic.
Reflexivity
[edit | edit source]Conditional and biconditional (but not conjunction and disjunction) are reflexive.
Commutativity
[edit | edit source]Conjunction, disjunction, and biconditional (but not conditional) are commutative.
Associativity
[edit | edit source]Conjunction, disjunction, and biconditional (but not conditional) are associative.
Distribution
[edit | edit source]We list ten distribution laws. Of these, probably the most important are that conjunction and disjunction distribute over each other and that conditional distributes over itself.
Transitivity
[edit | edit source]Conjunction, conditional, and biconditional (but not disjunction) are transitive.
Other tautologies and equivalences
[edit | edit source]Conditionals
[edit | edit source]These tautologies and equivalences are mostly about conditionals.
Biconditionals
[edit | edit source]These tautologies and equivalences are mostly about biconditionals.
Miscellaneous
[edit | edit source]We repeat DeMorgan's Laws from the Interdefinability of connectives section of Expressibility and add two additional forms. We also list some additional tautologies and equivalences.
- Idempotence for conjunction
- Idempotence for disjunction
- Disjunctive addition
- Disjunctive addition
-
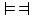 Demorgan's Laws
Demorgan's Laws -
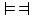 Demorgan's Laws
Demorgan's Laws -
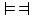 Demorgan's Laws
Demorgan's Laws -
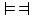 Demorgan's Laws
Demorgan's Laws -
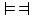 Double Negation
Double Negation
Deduction and reduction principles
[edit | edit source]The following two principles will be used in constructing our derivation system on a later page. They can easily be proven, but—since they are neither tautologies nor equivalences—it takes more than a mere truth table to do so. We will not attempt the proof here.
Deduction principle
[edit | edit source]Let and both be formulae, and let be a set of formulae.
Reduction principle
[edit | edit source]Let and both be formulae, and let be a set of formulae.
Substitution and Interchange
[edit | edit source]This page will use the notions of occurrence and subformula introduced at the Additional terminology section of Formal Syntax. These notions have been little used if at all since then, so you might want to review them.
Substitution
[edit | edit source]Tautological forms
[edit | edit source]We have introduced a number of tautologies, one example being
- (1)
Use the metavariables and to replace and in (1). This produces the form
- (2)
As it turns out, any formula matching this form is a tautology. Thus, for example, let and . Then,
- (3)
is a tautology. This process can be generalized to all tautologies: for any tautology, find its explicit form by replacing each sentence letters with distinct metavariables (written as Greek letters, as shown in (2)). We can call this a tautological form, which is a metalogical expression rather than a formula. Any instance of this tautological form is a tautology.
Substitution instances
[edit | edit source]The preceding illustrated how we can generate new tautologies from old ones via tautological forms. Here, we will show how to generate tautologies without resorting to tautological forms. To do this, we define a substitution instance of a formula. Any substitution instance of a tautology is also a tautology.
First, we define the simple substitution instance of a formula for a sentence letter. Let and be formulae and be a sentence letter. The simple substitution instance is the result of replacing every occurrence of in with an occurrence of . A substitution instance of formulae for a sentence letters is the result of a chain of simple substitution instances. In particular, a chain of zero simple substitutions instances starting from is a substitution instance and indeed is just itself. Thus, any formula is a substitution instance of itself.
It turns out that if is a tautology, then so is any simple substitution instance . If we start with a tautology and generate a chain of simple substitution instances, then every formula in the chain is also a tautology. Thus any (not necessarily simple) substitution instance of a tautology is also a tautology.
Substitution examples
[edit | edit source]Consider (1) again. We substitute for every occurrence of in (1). This gives us the following simple substitution instance of (1):
- (4)
In this, we substitute for . That gives us (3) as a simple substitution instance of (4). Since (3) is the result of a chain of two simple substitution instances, it is a (non-simple) substitution instance of (1) Since (1) is a tautology, so is (3). We can express the chain of substitutions as
Take another example, also starting from (1). We want to obtain
- (5)
Our first attempt might be to substitute for ,
- (6)
This is indeed a tautology, but it is not the one we wanted. Instead, we substitute for in (1), obtaining
Now substitute for obtaining
Finally, substituting for gets us the result we wanted, namely (5). Since (1) is a tautology, so is (5). We can express the chain of substitutions as
Simultaneous substitutions
[edit | edit source]We can compress a chain of simple substitutions into a single complex substitution. Let , , , ... be formulae; let , , ... be sentence letters. We define a simultaneous substitution instance of formulas for sentence letters be the result of starting with and simultaneously replacing with , with , .... We can regenerate our examples.
The previously generated formula (3) is
Similarly, (5) is
Finally (6) is
When we get to predicate logic, simultaneous substitution instances will not be available. That is why we defined substitution instance by reference to a chain of simple substitution instances rather than as a simultaneous substitution instance.
Interchange
[edit | edit source]Interchange of equivalent subformulae
[edit | edit source]We previously saw the following equivalence at Properties of Sentential Connectives:
You then might expect the following equivalence:
This expectation is correct; the two formulae are equivalent. Let and be equivalent formulae. Let be a formula in which occurs as a subformula. Finally, let be the result of replacing in at least one (not necessarily all) occurrences of with . Then and are equivalent. This replacement is called an interchange.
For a second example, suppose we want to generate the equivalence
We note the following equivalence:
These two formulae can be confirmed to be equivalent either by truth table or, more easily, by substituting for in both formulae of (7).
This substitution does indeed establish (9) as an equivalence. We already noted that and are equivalent if and only if is a tautology. Based on (7), we get the tautology
Our substitution then yields
which is also a tautology. The corresponding equivalence is then (9).
Based on (9), we can now replace the consequent of with its equivalent. This generates the desired equivalence, namely (8).
Every formula equivalent to a tautology is also a tautology. Thus an interchange of equivalent subformulae within a tautology results in a tautology. For example, we can use the substitution instance of (7):
together with the tautology previously seen at Properties of Sentential Connectives:
to obtain
as a new tautology.
Interchange example
[edit | edit source]As an example, we will use the interdefinability of connectives to express
- (10)
using only conditionals and negations.
Based on
we get the substitution instance
which in turn allows us to replace the appropriate subformula in (10) to get:
- (11)
The equivalence
together with the appropriate substitution gives us
- (12)
as equivalent to (11).
Finally, applying
together with the appropriate substitution, yields our final result:
Summary
[edit | edit source]This page has presented two claims.
- A substitution instance of a tautology is also a tautology.
- Given a formula, the result of interchanging a subformula with an equivalent is a formula equivalent to the given formula.
These claims are not trivial observations or the result of a simple truth table. They are substantial claims that need proof. Proofs are available in a number of standard metalogic textbooks, but are not presented here.
Translations
[edit | edit source]The page The Sentential Language gave a very brief look at translation between English and . We look at this in more detail here.
English sentential connectives
[edit | edit source]In the following discussion, we will assume the following assignment of English sentences to sentence letters:
- 2 is a prime number.
- 2 is an even number.
- 3 is an even number.
Not
[edit | edit source]The canonical translation of into English is 'it is not the case that'. Given the assignment above,
- (1)
translates as
- It is not the case that 2 is a prime number.
But we usually express negation in English simply by 'not' or by adding the contraction 'n't' to the end of a word. Thus (1) can also translate either of:
- 2 is not a prime number.
- 2 isn't a prime number.
If
[edit | edit source]The canonical translation of into English is 'if ... then ...'. Thus
- (2)
translates into English as
- (3) If 2 is a prime number, then 2 is an even number.
Objections have been raised to the canonical translation, and our example may illustrate the problem. It may seem odd to count (3) as true; however, our semantic rules does indeed count (2) as true (because both and are true). We might expect that, if a conditional and its antecedent are true, the consequent is true because the antecedent is. Perhaps we expect a general rule
- (4) if x is a prime number, then x is an even number
to be true—but this rule is clearly false. In any case, we often expect the truth of the antecedent (if it is indeed true) to be somehow relevant to the truth of the conclusion (if that is indeed true). (2) is an exception to the usual relevance of a number being prime to a number being even.
The conditional of is called the material conditional in contrast to strict conditional or counterfactual conditional. Relevance logic attempts to define a conditional which meets these objections. See also the Stanford Encyclopedia of Philosophy entry on relevance logic.
It is generally accepted today that not all aspects of an expression's linguistic use are part of its linguistic meaning. Some have suggested that the objections to reading 'if' as a material conditional are based on conversational implicature and so not based on the meaning of 'if'. See the Stanford Encyclopedia of Philosophy entry on implicature for more information. As much as a simplifying assumption than anything else, we will adopt this point of view. We can also point out in our defense that translations need not be exact to be useful. Even if our simplifying assumption is incorrect, is still the closest expression we have in to 'if'. It should also be noted that, in mathematical statements and proofs, mathematicians always use 'if' as a material conditional. They accept (2) and (3) as translations of each other and do not find it odd to count (3) as true.
'If' can occur at the beginning of the conditional or in the middle. The 'then' can be missing. Thus both of the following (in addition to (3)) translate as (2).
- If 2 is a prime number, 2 is an even number.
- 2 is an even number if 2 is a prime number.
Implies
[edit | edit source]We do not translate 'implies' into . In particular, we reject
- 2 is a prime number implies 2 is an even number.
as grammatically ill-formed and therefore not translatable as (2). See the Implication section of Validity for more details.
Only if
[edit | edit source]The English
- (5) 2 is a prime number only if 2 is an even number
is equivalent to the English
- If 2 is not an even number, then 2 is not a prime number.
This, in turn, translates into as
- (6)
We saw at Conditionals section of Properties of Sentential Connectives that (6) is equivalent to
- (7)
Many logic books give this as the preferred translation of (5) into . This allows the convenient rule ''if' always introduces an antecedent while 'only if' always introduces a consequent'.
Like 'if', 'only if' can appear in either the first or middle position of a conditional. (5) is equivalent to
- Only if 2 is an even number, is 2 a prime number.
Provided that
[edit | edit source]'Provided that'—and similar expressions such as 'given that' and 'assuming that'—can be use equivalently with 'if'. Thus each of the following translate into as (2).
- 2 is an even number provided that 2 is a prime number.
- 2 is an even number assuming that 2 is a prime number.
- Provided that 2 is a prime number, 2 is an even number.
Prefixing 'provided that' with 'only' works the same as prefixing 'if' with only. Thus each of the following translate into as (6) or (7).
- 2 is a prime number only provided that 2 is an even number.
- 2 is a prime number only assuming that 2 is an even number.
- Only provided that 2 is an even number, is 2 a prime number.
Or
[edit | edit source]The canonical translation of into English is '[either] ... or ...' (where the 'either' is optional). Thus
- (8)
translates into English as
- (9) 2 is a prime number or 2 is an even number
or
- Either 2 is a prime number or 2 is an even number.
We saw at the Interdefinability of connectives section of Expressibility that (8) is equivalent to
Just as there were objections to understanding 'if' as , there are similar objections to understanding 'or' as . We will again make the simplifying assumption that we can ignore these objections.
The English 'or' has both an inclusive and—somewhat controversially—an exclusive use. The inclusive or is true when at least one disjunct is true; the exclusive or is true when exactly one disjunct is true. The operator matches the inclusive use. The inclusive use becomes especially apparent in negations. If President Bush promises not to invade Iran or North Korea, not even the best Republican spin doctors will claim he can keep his promise by invading both. The exclusive reading of (9) translates into as
or more simply (and less intuitively) as
In English, telescoping is possible with 'or'. Thus, (8) translates
- 2 is either a prime number or an even number.
Similarly,
translates
- 2 or 3 is an even number.
Unless
[edit | edit source]'Unless' has the same meaning as 'if not'. Thus
- (10)
translates
- (11) 2 is a prime number unless 2 is an even number
and
- (12) Unless 2 is an even number, 2 is a prime number.
We saw at the Interdefinability of connectives section of Expressibility that (10) is equivalent to (8). Many logic books give (8) as the preferred translation of (11) or (12) into .
Nor
[edit | edit source]At the Joint denial section of Expressibility, we temporarily added to as the connective for joint denial. If we had that connective still available to us, we could translate
- Neither 2 is a prime number nor 2 is an even number
as
- .
However, since is not really in the vocabulary of , we need to paraphrase. Either of the following will do:
- (13) .
- (14) .
The same telescoping applies as with 'or'.
- 2 is neither a prime number nor an even number
translates into as either (13) or (14). Similarly,
- Neither 2 nor 3 is an even number
translates as either of
- .
- .
And
[edit | edit source]The canonical translation of into English is '[both] ... and ...' (where the 'both' is optional'). Thus
- (15)
translates into English as
- 2 is a prime number and 2 is an even number
or
- Both 2 is a prime number and 2 is an even number.
Our translation of 'and' as is not particularly controversial. However, 'and' is sometimes used to convey temporal order. The two sentences
- She got married and got pregnant.
- She got pregnant and got married.
are generally heard rather differently.
'And' has the same telescoping as 'or'.
- 2 is both a prime number and an even number
translates into as (15)
- Both 2 and 3 are even numbers
translates as
- .
If and only if
[edit | edit source]The canonical translation of into English is '... if and only if ...'. Thus
- (16)
translates into English as
- 2 is a prime number if and only if 2 is an even number.
The English sentence
- (17) 2 is a prime number if and only if 2 is an even number
is a shortened form of
- 2 is a prime number if 2 is an even number, and 2 is a prime number only if 2 is an even number
which translates as
or more concisely as the equivalent formula
- (18) .
We saw at the Interdefinability of connectives section of Expressibility that (18) is equivalent to (16). Issues concerning the material versus non-material interpretations of 'if' apply to 'if and only if' as well.
Iff
[edit | edit source]Mathematicians and sometimes others use 'iff' as an abbreviated form of 'if and only if'. So
- 2 is a prime number iff 2 is an even number
abbreviates (17) and translates as (16).
Examples
[edit | edit source]
Derivations
[edit | edit source]Derivations
[edit | edit source]In Validity, we introduced the notion of validity for formulae and for arguments. In sentential logic, a valid formula is a tautology. Up to now, we could show a formula to be valid (a tautology) in the following ways.
- Do a truth table for .
- Obtain as a substitution instance of a formula already known to be valid.
- Obtain by applying interchange of equivalents to a formula already known to be valid.
These methods fail in predicate logic, however, because truth tables are unavailable for predicates. Without an alternate method, we cannot use the second and third methods since they rely on knowing the validity of other formulas. An alternative method for showing a formula is valid—without using truth tables—is the use of derivations. This page and those that follow introduce this technique. Note, the claim that a derivation shows an argument valid assumes a sound derivation system, see soundness below.
A derivation is a series of numbered lines, each line consisting of a formula with an annotation. The annotations provide the justification for adding the line to the derivation. A derivation is a highly formalized analogue to—or perhaps a model of—a mathematical proof.
A typical derivation system will allow some of the following types of lines:
- A line may be an axiom. The derivation system may specify a set of formulae as axioms. These are accepted as true for any derivation. For sentential logic the set of axioms is a fixed subset of tautologies.
- A line may be an assumption. A derivation may have several types of assumptions. The following cover the standard cases.
- A premise. When attempting to show the validity of an argument, a premise of that argument may be assumed.
- A temporary assumption for use in a subderivation. Such assumptions are intended to be active for only part of a derivation and must be discharged (made inactive) before the derivation is considered complete. Subderivations will be introduced on a later page.
- A line may result from applying an inference rule to previous lines. An inference is a syntactic transformation of previous lines to generate a new line. Inferences are required to follow one of a fixed set of patterns defined by the derivation system. These patterns are the system's inference rules. The idea is that any inference fitting an inference rule should be a valid argument.
Soundness and validity
[edit | edit source]We noted in Formal Semantics that a formal language such as can be interpreted via several alternative and even competing semantic rule-sets. Multiple derivation systems can be also defined for a given syntax-semantics pair. A triple consisting of a formal syntax, a formal semantics, and a derivation system is a logical system.
A derivation is intended to show an argument to be valid. A derivation of a zero-premise argument is intended to show its conclusion to be a valid formula—in sentential logic this means showing it to be a tautology. Given a logical system, the derivation system is called sound if it achieves these goals. That is, a derivation system is sound (has the property of soundness) if every formula (and argument) derivable in its derivation system is valid (given a syntax and a semantics).
Another desirable quality of a derivation system is completeness. Given a logical system, its derivation system is said to be complete if every valid formula is derivable. However, there are some logics for which no derivation system is or can be complete.
Soundness and completeness are substantial results. Their proofs will not be given here, but are available in many standard metalogic text books.
Turnstiles
[edit | edit source]The symbol is sometimes called a turnstile, in particular a semantic turnstile. We previously introduced the following three uses of this symbol.
| (1) | satisfies . | ||||
| (2) | is valid. | ||||
| (3) | implies (has as a logical consequence) . |
where is a valuation and is a set of premises, as introduced in Validity.
Derivations have a counterpart to the semantic turnstile, namely the syntactic turnstile. Item (1) above has no syntactic counterpart. However, (2) and (3) above have the following counterparts.
| (4) | is provable. | ||||
| (5) | proves (has as a derivational consequence) . |
Item (4) is the case if and only if there is a correct derivation of from no premises. Similarly, (5) is the case if and only if there is a correct derivation of which takes the members of as premises.
The negations of (4) and (5) above are
| (6) | |||
| (7) |
We can now define soundness and completeness as follows:
- Given a logical system, its derivation system is sound if and only if:
- Given a logical system, its derivation system is complete if and only if:
Inference Rules
[edit | edit source]Overview
[edit | edit source]Inference rules will be formated as in the following example.
- Conditional Elimination (CE)
The name of this inference rule is 'Conditional Elimination', which is abbreviated as 'CE'. We can apply this rule if formulae having the forms above the line appear as active lines of text in the derivation. These are called the antecedent lines for this inference. Applying the rule adds a formula having the form below the line. This is called the consequent line for this inference. The annotation for the newly derived line of text is the line numbers of the antecedent lines and the abbreviation 'CE'.
Note. You might see premise line and conclusion line for antecedent line and consequent line. You may see other terminology as well, as most textbooks avoid giving any special terminology here.
Each sentential connective will have two inference rules, one each of the following types.
- An introduction rule. The introduction rule for a given connective allows us to derive a formula having the given connective as its main connective.
- An elimination rule. The elimination rule for a given connective allows us to use a formula already appearing in the derivation having the given connective as its main connective.
Three rules (Negation Introduction, Negation Elimination, and Conditional Introduction) will be deferred to a later page. These are so-called discharge rules which will be explained when we get to subderivations.
Three rules (Conjunction Elimination, Disjunction Introduction, and Biconditional Elimination) will have two forms each. We somewhat arbitrarily count the two patterns as forms of the same rule rather than separate rules.
The validity of the inferences on this page can be shown by truth table.
Inference rules
[edit | edit source]Negation
[edit | edit source]Negation Introduction (NI)
- Deferred to a later page.
Negation Elimination (NE)
- Deferred to a later page.
Conjunction
[edit | edit source]Conjunction Introduction (KI)
Conjunction Introduction traditionally goes by the name Adjunction or Conjunction.
Conjunction Elimination, Form I (KE)
Conjunction Elimination, Form II (KE)
Conjunction Elimination traditionally goes by the name Simplification.
Disjunction
[edit | edit source]Disjunction Introduction, Form I (DI)
Disjunction Introduction, Form II (DI)
Disjunction Introduction traditionally goes by the name Addition.
Disjunction Elimination (DE)
Disjunction Elimination traditionally goes by the name Separation of Cases.
Conditional
[edit | edit source]Conditional Introduction (CI)
- Deferred to a later page.
Conditional Elimination (CE)
Conditional Elimination traditionally goes by the Latin name Modus Ponens or, less often, by Affirming the Antecedent.
Biconditional
[edit | edit source]Biconditional Introduction (BI)
Biconditional Elimination, Form I (BE)
Biconditional Elimination, Form II (BE)
Examples
[edit | edit source]Inference rules are easy enough to apply. From the lines
- (1)
and
- (2)
we can apply Conditional Elimination to add
- (3)
to a derivation.
The annotation will be the line numbers of (1) and (2) and the abbreviation for Conditional Elimination, namely '1, 2, CE'. The order of the antecedent lines does not matter; the inference is allowed regardless of whether (1) appears before or after (2).
It must be remembered that inference rules are strictly syntactical. Semantically obvious variations is not allowed. It is not allowed, for example, to derive (3) from (1) and
- (4)
However, you can get from (1) and (4) to (3) by first deriving
- (5)
and
- (6)
by Conjunction Elimination (KE). Then you can derive (2) by Conjunction Introduction (KI) and finally (3) from (1) and (2) by Conditional Elimination (CE) as before. Some derivation systems have a rule, often called Tautological Implication, allowing you to derive any tautological consequence of previous lines. However, this should be seen as an (admittedly useful) abbreviation. On later pages, we will implement a restricted version of this abbreviation.
It is generally useful to apply break down premises, other assumptions (to be introduced on a later page) by applying elimination rules—and then continue breaking down the results. Supposing that is why we applied CE to (1) and (2), it will likely be useful to derive
- (7)
and
- (8)
by applying Biconditional Elimination (BE) to (3). To further break this down, you might then attempt to derive or so that you can apply CE to (7) or (8).
If you know what line you want to derive, you can build it up by applying introduction rules. That was the strategy for deriving (2) from (5) and (6).
Constructing a Simple Derivation
[edit | edit source]Our derivations consists two types of elements.
- Derived lines. A derived line has three parts:
- Line number. This allows the line to be referred to later.
- Formula. The purpose of a derivation is to derive formulae, and this is the formula that has been derived at this line.
- Annotation. This specifies the justification for entering the formula into the derivation.
- Fencing. These include:
- Vertical lines between the line number and the formula. These are used to set off subderivations which we will get to in the next module.
- Horizontal lines separating premises and temporary assumptions from other lines. When we get to predicate logic, there are restrictions on using premises and temporary assumptions. Setting them off in an easy-to-recognize fashion aids in adhering to the restrictions.
We often speak informally of the formula as if it were the entire line, but the line also includes the line number and the annotation.
Rules
[edit | edit source]Premises
[edit | edit source]The annotation for a premise is 'Premise'. We require that all premises used in the derivation are in the first lines. No non-premise line is allowed to appear before a premise. In theory, an argument can have infinitely many premises. However, derivations have only finitely many lines, so only finitely many premises can be used in the derivation. We do not require that all premises appear before other lines. This would be impossible for arguments with infinitely many premises. But we do require that all premises to appear in the derivation appear before any other line.
The requirement that premises used in the derivation appear as its first lines is stricter than absolutely necessary. However, certain restrictions that will be needed when we get to predicate logic make the requirement at least a useful convention.
Inference rules
[edit | edit source]We introduced all but two inference rules in the previous module, and will introduce the other two in the next module.
Axioms
[edit | edit source]This derivation system does not have any axioms.
An example derivation
[edit | edit source]We will construct a derivation for the following argument:
- ∴
First, we enter the premises into the derivation:
|
Note the vertical line between the line numbers and the formulae. That is part of the fencing that controls
subderivations. We will get to subderivations in the next module. Until then, we simply put a single vertical line the length of the derivation. Note also the horizontal line under the premises. This is fencing that helps distinguish
the premises from the other lines in the derivation.
Now we need to use the premises. Applying KE to the first premise twice. we add the following lines:
|
Now we need to use the second premise by applying CE. Since CE has two antecedent lines, we first need to derive the other line that we will need. We thus add these lines:
|
Now we will use the third premise by applying CE. Again, we first need to derive the other line we will need. The
new lines are:
|
Line 9 is , the conclusion of our argument, so we are done. The
conclusion does not always fall into our lap so nicely, but here it did. The complete derivation runs:
|
Subderivations and Discharge Rules
[edit | edit source]As already seen, we need three more inference rules, Conditional Introduction (CI), Negation Introduction (NI), and Negation Elimination (NE). These require subderivations.
Deriving conditionals
[edit | edit source]Example derivation
[edit | edit source]We begin with an example derivation which illustrates Conditional Introduction, then follow with an explanation. A derivation for the argument
- ∴
is as follows:
|
Lines 2 and 3 constitute a subderivation. It starts by assuming desired formula's antecedent and ends by deriving the desired formula's consequent. There are two vertical fences between the line numbers and the formulae to set it off from the rest of the derivation and to indicate its subordinate status. Line 2 has a horizontal fence under it to separate the assumption from the rest of the subderivation. Line 4 is the application of Conditional Introduction. It follows not from one or two individual lines but from the entire subderivation (lines 2–3) as a whole.
Conditional Introduction is a discharge rule. It discharges (makes inactive) that assumption and indeed makes the entire subderivation inactive. Once we apply a discharge rule, no line from the subderivation (here, lines 2 and 3) can be further used in the derivation.
The Conditional Introduction rule
[edit | edit source]To derive a formula , the rule of Conditional Introduction (CI) is applied by first assuming in a subderivation that the antecedent is true, then deriving as the conclusion of the subderivation. Symbolically, CI is written as
Here, the consequent line is not inferred from one or more antecedent lines, but from a subderivation as a whole. The annotation is the range of lines occupied by the subderivation and the abbreviation CI. Unlike previously introduced inference rules, Conditional Introduction cannot be justified by a truth table. Rather it is justified by the Deduction Principle introduced at Properties of Sentential Connectives. The intuition behind why we assume in order to derive , however, is that is true by definition if is false. Thus, if we show is true whenever happens to be true, then must be true.
Note that the antecedent subderivation can consist of a single line serving both as the assumed and the derived , as in the following derivation of
- ∴
|
Negations
[edit | edit source]Example derivation
[edit | edit source]To illustrate Negation Introduction, we will provide a derivation for the argument
- ∴
|
Lines 3 through 6 constitute a subderivation. It starts by assuming the desired formula's opposite and ends by assuming a contradiction (a formula and its negation). As before, there are two vertical fences between the line numbers and the formulae to set it off from the rest of the derivation and to indicate its subordinate status. And the horizontal fence under line 3 again separates the assumption from the rest of the subderivation. Line 7, which follows from the entire subderivation, is the application of Negation Introduction.
At line 9, note that the annotation '5 DI' would be incorrect. Although inferring from is valid by DI, line 5 is no longer active when we get to line 9. Thus we are not allowed to derive anything from line 5 at that point.
The Negation Introduction rule
[edit | edit source]Negation Introduction (NI)
The consequent line is inferred from the whole subderivation. The annotation is the range of lines occupied by the subderivation and the abbreviation is NI. Negation Introduction sometimes goes by the Latin name Reductio ad Absurdum or sometimes by Proof by Contradiction.
Like Conditional Introduction, Negation Introduction cannot be justified by a truth table. Rather it is justified by the Reductio Principle introduced at Properties of Sentential Connectives.
Another example derivation
[edit | edit source]To illustrate Negation Elimination, we will provide a derivation for the argument
- ∴
|
Lines 2 through 4 constitute a subderivation. As in the previous example, it starts by assuming the desired formula's opposite and ends by assuming a contradiction (a formula and its negation). Line 5, which follows from the entire subderivation, is the application of Negation Elimination.
The Negation Elimination rule
[edit | edit source]Negation Elimination (NE)
The consequent line is inferred from the whole subderivation. The annotation is the range of lines occupied by the subderivation and the abbreviation is NE. Like Negation Introduction, Negation Elimination sometimes goes by the Latin name Reductio ad Absurdum or sometimes by Proof by Contradiction.
Like Negation Introduction, Negation Elimination is justified by the Reductio Principle introduced at Properties of Sentential Connectives. This rule's place in the Introduction/Elimination naming convention is somewhat more awkward than for the other rules. Unlike the other elimination rules, the negation that gets eliminated by this rule does not occur in an already derived line. Rather the eliminated negation occurs in the assumption of the subderivation.
Terminology
[edit | edit source]The inference rules introduced in this module, Conditional Introduction and Negation Introduction, are discharge rules. For lack of a better term, we can call the inference rules introduced in Inference Rules 'standard rules'. A standard rule is an inference rule whose antecedent is a set of lines. A discharge rule is an inference rule whose antecedent is a subderivation.
The depth of a line in a derivation is the number of fences standing between the line number and the formula. All lines of a derivation have a depth of at least one. Each temporary assumption increases the depth by one. Each discharge rule decreases the depth by one.
An active line is a line that is available for use as an antecedent line for a standard inference rule. In particular, it is a line whose depth is less than or equal to the depth of the current line. An inactive line is a line that is not active.
A discharge rule is said to discharge an assumption. It makes all lines in its antecedent subderivation inactive.
Constructing a Complex Derivation
[edit | edit source]An example derivation
[edit | edit source]Subderivations can be nested. For an example, we provide a derivation for the argument
- ∴
We begin with the premises and then assume the antecedent of the conclusion.
Note. Each time we begin a new subderivation and enter a temporary assumption, there is a specific formula we are hoping to derive when it comes time to end the derivation and discharge the assumption. To make things easier to follow, we will add this formula to the annotation of the assumption. That formula will not officially be part of the annotation and does not affect the correctness of the derivation. Instead, it will serve as an informal reminder to ourselves noting where we are going.
|
This starts a subderivation to derive the argument's conclusion. Now we will try a Disjunction Elimination (DE) to derive its consequent:
This will require the showing two conditionals we need for the antecedent lines of a DE, namely:
and
We begin with the first of these conditionals.
|
This subderivation is easily finished.
|
Now we are ready to discharge the two assumptions at Lines 5 and 6.
|
Now it's time for the second conditional needed for our DE planned back at Line 4. We begin.
|
Note that we have a contradiction between Lines 12 and 15. But line 12 is in the wrong place. We need it in the same subderivation as Line 15. A silly trick at Lines 16 and 17 below will accomplish that. Then the assumptions at Lines 12 and 13 can be discharged.
|
Finally, with Lines 4, 11, and 19, we can perform the DE we've been wanting since Line 4.
|
Now to finish the derivation by discharging the assumption at Line 4.
|
The complete derivation
[edit | edit source]Here is the completed derivation.
|
Theorems
[edit | edit source]A theorem is a formula for which a zero-premise derivation has been provided. We will keep a numbered list of proved theorems. In the derivations that follow, we will continue our informal convention of adding a formula to the annotations of assumptions, in particular the formula we hope to derive by means of the newly started subderivation.
An example
[edit | edit source]You may remember from Constructing a Complex Derivation that we had to employ a silly trick to copy a formula into the proper subderivation (Lines 16 and 17). We can prove a theorem that will help us avoid such obnoxiousness.
|
Derivations can be abbreviated by allowing a line to be entered whose formula is a substitution instance of a previously proved theorem. The annotation will be 'Tn' where n is the number of the theorem. Although we won't require it officially, we will also show the substitution, if any, in the annotation (see Line 3 in the derivation below). The proof of the next theorem will use T1.
|
Justification: Converting to unabbreviated derivation
[edit | edit source]We need to justify using theorems in derivations in this way. To do that, we show how to produce a correct, unabbreviated derivation of T2, one without citing the theorem we used in its abbreviated proof.
Observe that when we entered Line 3 into our derivation of T2, we substituted for in T1. Suppose you were to apply the same substitution on each line of our proof for T1. You would then end up with the following equally correct derivation.
|
Suppose now you were to replace Line 3 of our proof for T2 with this derivation. You would need to adjust the line numbers so that you would have only one line per line number. You would also need to adjust the annotations so the line numbers they would continue to refer correctly. But, with these adjustments, you would end up with the following correct unabbreviated derivation of T2.
|
Thus we see that entering a previously proved theorem into a derivation is simply an abbreviation for including that theorem's proof into a derivation. The instructions above for unabbreviating a derivation could be made more general and more rigorous, but we will leave them in this informal state. Having instructions for generating a correct unabbreviated derivation justifies entering previously proved theorems into derivations.
Additional theorems
[edit | edit source]Additional theorems will be introduced over the next two modules.
Derived Inference Rules
[edit | edit source]This page introduces the notion of a derived inference rule and provides a few such rules.
Deriving inference rules
[edit | edit source]The basics
[edit | edit source]Now we can carry the abbreviation a step further. A derived inference rule is an inference rule not given to us as part of the derivation system but which constitutes an abbreviation using a previously proved theorem. In particular, suppose we have proved a particular theorem. In this theorem, uniformly replace each sentence letter with a distinct Greek letter. Suppose the result has the following form.
- .
[Comment: This and what follows seems to me to be potentially confusing to students. The intention stated in earlier sections to avoid metatheory creates a problem here as one needs to know about the Deduction Theorem for this to make more sense.]
We may then introduce a derived inference rule having the form
An application of the derived rule can be eliminated by replacing it with
- the previously proved theorem,
- repeated applications of Conjunction Introduction (KI) to build up the theorem's antecedent, and
- an application of Conditional Elimination (CE) to obtain the theorem's consequent.
The previously proved theorem can then be eliminated as described above. That would leave you with an unabbreviated derivation.
Removing abbreviations from a derivation is not desirable, of course, because it makes the derivation more complicated and harder to read, but the fact that a derivation could be unabbreviated justifies the use of abbreviations, so that we can employ abbreviations in the first place.
Repetition
[edit | edit source]Our first derived inference rule will be based on T1, which is
Replace the sentence letters with Greek letters, and we get:
We now generate the derived inference rule:
- Repetition (R)
Now we can show how this rule could have simplified our proof of T2.
|
While this is only one line shorter than our original proof of T2, it is less obnoxious. We can use an inference rule instead of a silly trick. As a result, the derivation is easier to read and understand (not to mention easier to produce).
Double negation rules
[edit | edit source]The next two theorems—and the derived rules based on them—exploit the equivalence between a doubly negated formula and the unnegated formula.
Double Negation Introduction
[edit | edit source]
|
T3 justifies the following rule.
- Double Negation Introduction (DNI)
Double Negation Elimination
[edit | edit source]
|
T4 justifies the following rule.
- Double Negation Elimination (DNE)
Additional derived rules
[edit | edit source]Contradiction
[edit | edit source]
|
Our next rule is based on T5.
- Contradiction (Contradiction)
This rule is occasionally useful when you have derived a contradiction but the discharge rule you want is not NI or NE. This then avoids a completely trivial subderivation. The rule of Contradiction will be used in the proof of the next theorem.
Conditional Addition
[edit | edit source]
|
On the basis of T2 and T6, we introduce the following derived rule.
- Conditional Addition, Form I (CAdd)
- Conditional Addition, Form II (CAdd)
The name 'Conditional Addition' is not in common use. It is based on the traditional name for Disjunction Introduction, namely 'Addition'. This rule does not provide a general means of introducing a conditional. This is because the antecedent line you would need is not always derivable. However, when the antecedent line just happens to be easily available, then applying this rule is simpler than producing the subderivation needed for a Conditional Introduction.
Modus Tollens
[edit | edit source]
|
Now we use T7 to justify the following rule.
- Modus Tollens (MT)
Modus Tollens is also sometimes known as 'Denying the Consequent'. Note that the following is not an instance of Modus Tollens, at least as defined above.
The premise lines of Modus Tollens are a conditional and the negation of its consequent. The premise lines of this inference are a conditional and the opposite of its consequent, but not the negation of its consequent. The desired inference here needs to be derived as below.
|
Of course, it is possible to prove as a theorem:
Then you can add a new inference rule—or, more likely, a new form of Modus Tollens—on the basis of this theorem. However, we won't do that here.
Additional theorems
[edit | edit source]The derived rules given so far are quite useful for eliminating frequently used bits of obnoxiousness in our derivations. They will help to make your derivations easier to generate and also more readable. However, because they are indeed derived rules, they are not strictly required but rather are theoretically dispensable.
A number of other theorems and derived rules could usefully be added. We list here some useful theorems but leave their proofs and the definition of their associated derived inference rules to the reader. If you construct many derivations, you may want to maintain your own personal list that you find useful.
Theorems with biconditionals
[edit | edit source]Theorems with negations
[edit | edit source]
Disjunctions in Derivations
[edit | edit source]Disjunctions in derivations are, as the current inference rules stand, difficult to deal with. Using an already derived disjunction by applying Disjunction Elimination (DE) is not too bad, but there is an easier to use alternative. Deriving a disjunction in the first place is more difficult. Our Disjunction Introduction (DI) rule turns out to be a rather anemic tool for this task. In this module, we introduce derived rules which provide alternative methods for dealing with disjunctions in derivations.
Using already derived disjunctions
[edit | edit source]Modus Tollendo Ponens
[edit | edit source]We start with a new (to be) derived rule of inference. This will provide a useful alternative to Disjunction Elimination (DE).
- Modus Tollendo Ponens, Form I (MTP)
- Modus Tollendo Ponens, Form II (MTP)
Modus Tollendo Ponens is sometimes known as Disjunctive Syllogism and occasionally as the Rule of the Dog.
Supporting theorems
[edit | edit source]This new rule requires the following two supporting theorems.
|
|
Example derivation
[edit | edit source]For an example using MTP, we redo the example derivation from Constructing a Complex Derivation.
- ∴
|
After Line 4, we did not bother with subderivations for deriving the antecedent lines needed for DE. Instead, we went straight to a subderivation for the conclusion's consequent. At line 8, we applied MTP.
Deriving disjunctions
[edit | edit source]Conditional Disjunction
[edit | edit source]The next derived rule significantly reduces the labor of deriving disjunctions, thus providing a useful alternative to Disjunction Introduction (DI).
- Conditional Disjunction (CDJ)
Supporting theorem
[edit | edit source]
|
Example derivation
[edit | edit source]This derivation will make use of T12 (introduced at Derived Inference Rules) even though its proof was left to the reader as an exercise. The correctness the following derivation, particularly Line 2, assumes that you have indeed proved T12.
- ∴
|
Here we attempted to derive the desired conditional by first deriving the antecedent line needed for CDJ.
Goals
[edit | edit source]Sentential logic treated whole sentences and truth functional relations among them. Predicate logic treats more fine-grained logical features. This page will informally describe of the logic features of English captured by predicate logic.
Predicate logic goals
[edit | edit source]Predicates and terms
[edit | edit source]We distinguish between predicates and terms. The simplest terms are simple names such as 'one', 'Socrates', or 'Pegasus'. Simple predicates attribute properties to the object named. In
- Socrates is bald.
'Socrates' is a name and 'is bald' is the predicate. We can informally exhibit its logical structure with
- Bald(socrates)
There are also more complex terms such as '3 minus 2', 'the father of Socrates', and '3 divided by 0'. The logical structure of these can be exhibited informally by
- minus(3, 2)
- father(socrates)
- quotient(3, 0)
These more complex terms can be used to construct sentences such as
- 3 minus 2 is even.
- The father of Socrates is bald.
- 3 divided by zero is odd.
Their logical structure can be informally exhibited by
- Even( minus(3, 2) )
- Bald( father(Socrates) )
- Odd( quotient(3, 0) )
There are also complex predicates, often called relations. Sentences using such predicates include
- 3 is greater than 2
- Socrates is a child of the father of Socrates and the mother of Socrates.
- Pegasus kicked Bucephalus.
Their logical structures can be informally exhibited as
- Greater_than(3, 2)
- Child(socrates, father(socrates), mother(socrates))
- Kicked(pegasus, bucephalus)
General statements
[edit | edit source]Names and other terms refer to specific objects. We can also speak generally of all objects or of some (at least one) objects. Some examples are:
- All numbers are prime.
- Some numbers are prime.
- Some numbers are not prime.
- No numbers are prime.
The logical structures of the first three can be informally exhibited as
- All x (if Number(x), then Prime(x)).
- Some x (Number(x) and Prime(x)).
- Some x (Number(x) and not( Prime(x))).
The fourth can have its logical structure exhibited either as
- All x (if Number(x), then not Prime(x).
or, equivalently, as
- Not (some x (Number(x) and Prime(x))).
Note that we count
- All unicorns have a horn
as trivially true because there are no unicorns. In addition, we take 'some' to mean at least one (not, as might be expected, at least two). Thus we take
- Some prime numbers are even
to be true even though two is the only even prime.
More complexity
[edit | edit source]Variables such as 'x' and 'y' help us to keep the following straight.
- All x all y (if Person(x) and Person(y), then Loves(x, y))
- All x all y (if Person(y) and Person(x), then Loves(y, x))
- These are equivalent and both say that everybody loves everybody.
- Some x some y (Person(x) and Person(y) and Loves(x, y))
- Some x Some y (Person(y) and Person(x) and Loves(y, x))
- These are equivalent and both say that somebody loves someone.
- All x (if Person(x), then some y (Person(y) and Loves(x, y)))
- Some y (Person(y) and all x (if Person(x), then Loves(x, y)))
- The first says that everybody loves somebody (or other—they do not necessarily all love the same person). The second says that somebody is loved by everybody. Thus the second, but not the first, requires a universally loved person.
- All x (if Person(x), then some y (Person(y) and Loves(y, x)))
- Some y (Person(y) and all x (if Person(x), then Loves(y, x)))
- The first says that that everybody is loved by somebody (or other—not necessarily all loved by the same person). The second says that the somebody loves everybody. Thus the second, but not the first, requires a universal lover.
Domains
[edit | edit source]By convention, we can temporarily limit the range of the objects being considered. For example, a policy of speaking only about people might be conventionally adopted. Such a convention would allow us to hope optimistically that
- All x some y Loves(y, x)
without hoping that cups and saucers are thereby loved. The truth or falsity of a sentence can be evaluated within the context of such a convention or policy. In a different context, a different convention might prove more convenient. For example, the policy of only speaking about people would prevent us from saying
- Loves( alexander_the_great, beaucephalus)
However, widening the domain to include both horses and people does allow us to say this.
We call the range of objects under discussion the domain, or sometimes the domain of discourse. A sentence that is true in the context of one domain may be false in the context of another.
Limits
[edit | edit source]There are two limits on predicate logic as conventionally developed and indeed as will be developed here.
- First, predicate logic assumes that at least one thing exists. We cannot, for example, limit the domain of discourse to unicorns.
- Second names and complex terms must refer to objects in the domain. Thus we cannot use such terms as
- Pegasus
- 3 divided by 0
In addition, if we limit the domain to natural numbers, we cannot use a term such as
- 2 minus 3
The loss of '3 divided by 0' in turn requires predicate logic to avoid forming any term with 'divided by'. The loss of '2 minus 3' requires predicate logic to avoid forming any term with 'minus' except in the context of domains including negative numbers.
The significance of these limits is controversial. Free Logic attempts to avoid such limits. The Stanford Encyclopedia of Philosophy has an entry on free logic.
The Predicate Language
[edit | edit source]This page informally describes our predicate language which we name . A more formal description will be given in subsequent pages.
Language components
[edit | edit source]Use of occurs in the context of a domain of objects. Ascribing a property to 'everything' is only interpreted as ascribing it to everything in the domain.
Definitions
[edit | edit source]Variables serve as placeholders in general statements for objects in the domain of discourse. We will use the lower case letters n through z as variables. Frequently, variables correspond to pronouns in statements. For instance, consider the statement 'For any number, if it is even then it is not odd.' Introducing the variable x produces 'For any number x, if x is even then x is not odd.'
An operation letter is a function that takes a fixed number of objects (or variables representing objects) and returns an object in the domain. We write operation letters as lower case letters a through m. An operation letter that takes n objects is called an n-place operation letter. Zero-place operation letters are allowed and merely represent a fixed object. Usually, the context is sufficient to determine the number of places of each operation letter.
For examples on this page, we also allow numerals () as zero-place operation letters.
A term is any of the following:
- A variable
- A zero-place operation letter.
- An n-place operation letter (with ) followed by a parenthesized list of n terms.
Examples include (variables); (zero-place operation letters); (1-place operation letter operating on ); and (2-place operation letter operating on and ).
If a term contains no variables, then it is called a name. Each name specifies a particular object in the domain, whereas terms containing variables do not.
Examples
[edit | edit source]For the remainder of this page, assume the following translations.
With the right set of characters in the domain, names Cain, and (according to Biblical tradition) names Adam.
The term is not a name because it contains variables. Then the terms and , however, name 7 and 3 respectively (assuming that 7 and 3 are in the domain).
Primitive formulae
[edit | edit source]A predicate letter is a function that takes a fixed number of objects (or variables representing objects) and returns a sentence letter. Predicate letters will consist of capital letters A through Z. The same symbols will be used for predicate letters of any number of places, so, as with operation letters, we sometimes need to specify the number of places but usually can rely on context. Notice that zero-place predicate letters are sentence letters we are familiar with from sentential logic.
A primitive formulae is either one of the following:
- A zero-place predicate letter (that is, a sentence letter).
- An n-place predicate letter (with ) followed by a parenthesized list of n terms.
Examples include
Examples
[edit | edit source]

If translates 'Snow is white', then it is true. However, it is false if it translates 'Snow is blue'.
Suppose we add the following translations to the translations above:
We say that is true of all bald things and false of all non-bald things. Thus is true while is false. Whether is true or false depends on whether Adam was bald.
Now add
to the translations above. Then is neither true nor false because and are variables that do not name anything, nor do the variables or . But if we substitute numbers for the variables, then the is true while is false.
Sentential connectives
[edit | edit source]The predicate language will use sentential connectives just as they were used in the sentential language . These were:
Using the translations already set above (together with letting numerals be zero-place operation letters),
is true while
is false.
Quantifiers
[edit | edit source]Quantifiers are special symbols that allow us to construct general sentences which are about all thing or about some (at least one) things.
- translates to English as 'for all x'.
- is called a universal generalization.
- is true if is true of all objects in the domain. Roughly speaking, it is true if
- where each names an object in the domain and all objects in the domain are named. This is only a rough characterization, however. First, we do not require that all objects in the domain have a name in the predicate language. Second, we allow there to be infinitely many objects in the domain but do not allow infinitely long sentences.
- Some authors use instead of . This notation is semi-obsolete and is becoming ever less frequent.
- translates to English as 'there exists an x' or, perhaps a bit more clearly, 'there exists at least one x'.
- is called an existential generalization.
- is true if is true of at least one object in the domain. Roughly speaking, it is true if
- where each names an object in the domain and all objects in the domain are named. This is only a rough characterization, however. First, we do not require that all objects in the domain have a name in the predicate language. Second, we allow there to be infinitely many objects in the domain but do not allow infinitely long sentences.
Translation
[edit | edit source]Using the translation scheme
we translate as follows.
- All numbers are prime.
- Some numbers are prime.
- No numbers are prime. (two equivalent alternatives are given)
- Some numbers are not prime.
Now using the translation scheme
we can translate as follows.
- George loves Martha.
- Martha loves George.
- George and Martha love each other.
We can further translate as follows.
- Everybody loves everybody. (the second alternative assumes only persons in the domain)
- Somebody loves somebody. (the second alternative assumes only persons in the domain)
- Everybody loves somebody (or other). (the second alternative assumes only persons in the domain)
- Somebody is loved by everybody. (the second alternative assumes only persons in the domain)
- Everybody is loved by somebody (or other). (the second alternative assumes only persons in the domain)
- Somebody loves everybody. (the second alternative assumes only persons in the domain)
Formal Syntax
[edit | edit source]In The Predicate Language, we informally described our sentential language. Here we give its formal syntax or grammar. We will call our language . This is an expansion of the sentential language and will include as a subset.
Vocabulary
[edit | edit source]- Variables: Lower case letters 'n'–'z' with a natural number subscript. Thus the variables are:
- Operation letters: Lower case letters 'a'–'m' with (1) a natural number superscript and (2) a natural number subscript.
- A constant symbol is a zero-place operation letter. This piece of terminology is not completely standard.
- Predicate letters: Upper case letters 'A'–'Z' with (1) a natural number superscript and (2) a natural number subscript.
- A sentence letter is a zero-place predicate letter.
- Sentential connectives:
- Quantifiers:
- Grouping symbols:
The superscripts on operation letters and predicate letters indicate the number of places and are important for formation rules. The subscripts on variables, operation letters, and predicate letters are to ensure an infinite supply of symbols in these classes. On a subsequent page we will abbreviate away most superscript use by letting the context make the number of places clear. We will also abbreviate away most subscript use by letting a symbol without a subscript abbreviate one with the subscript '0'. For now, though, we stick with the unabbreviated form.
The sentence letters of sentential logic are zero-place predicate letters, namely, predicate letters with the superscript '0'. The vocabulary of , the sentential logic formal language, includes zero-place predicate letters, sentential connectives, and grouping symbols.
Expressions
[edit | edit source]Any string of symbols from is an expression. Not all expressions are grammatically well-formed. The primary well-formed expression is a formula. However, there are also well-formed entities that are smaller than formulae, namely quantifier phrases and terms.
Formation rules
[edit | edit source]Quantifier phrases
[edit | edit source]A quantifier phrase is a quantifier followed by a variable. The following are examples:
Terms
[edit | edit source]An expression of is a term of if and only if it is constructed according to the following rules.
- A variable is a term.
- A constant symbol (zero-place operation letter, i.e., an operation letter with the superscript '0') is a term.
- If is an n-place operation letter (n greater than 0) and are terms, then
- is a term.
A name is a term with no variables.
Formulae
[edit | edit source]An expression of is a well-formed formula of if and only if it is constructed according to the following rules.
- A sentence letter (a zero-place predicate letter) is a well-formed formula.
- If is an n-place predicate letter (n greater than 0) and are terms, then
- is a well-formed formula.
- If and are well-formed formulae, then so are each of:
- If is a well-formed formula and is a variable, then each of the following is a well-formed formula:
In general, we will use 'formula' as shorthand for 'well-formed formula'. We will see in the section Free and Bound Variables that only some formulae are sentences.
Additional terminology
[edit | edit source]A few of these terms are repeated from above. All definitions from the sentential logic additional terminology section apply here except the definitions of 'atomic formula' and 'molecular formula'. These latter two terms are redefined below.
A constant symbol is a zero-place operation letter. (Note that different authors will vary on this.)
A name is a term in which no variables occur. (Note that different authors will vary on this. Some use 'name' only for zero-place operation letters, and some prefer to avoid the word altogether.)
A sentence letter is a zero-place predicate letter.
The universal quantifier is the symbol . The existential quantifier is the symbol .
A quantified formula is a formula that begins with a left parenthesis followed by a quantifier. A universal generalization is a formula that begins with a left parenthesis followed by a universal quantifier. An existential generalization is a formula that begins with a left parenthesis followed by an existential quantifier.
An atomic formula is one formed solely by formula formation clause {i} or {ii}. Put another way, an atomic formula is one in which no sentential connectives or quantifiers occur. A molecular formula is one that is not atomic. Thus a molecular formula has at least one occurrence of either a sentential connective or a quantifier. (Revised from sentential logic.)
A prime formula is a formula that is either an atomic formula or a quantified formula. A non-prime formula is one that is not prime. (Note that this is not entirely standard terminology. It has been used this way by some authors, but not often.)
The main operator of a molecular formula is the last occurrence of a sentential connective or quantifier added when the formula was constructed according to the rules above. If the main operator is a sentential connective, then it is also called the 'main connective' (as was done in the sentential language ). However, there is a change as we move to . In predicate logic, it is no longer true that all molecular formulae have a main connective. Some main operators are now quantifiers rather than sentential connectives.
Examples
[edit | edit source]Example 1
[edit | edit source]By clause (i) in the definition of 'term', and are terms. Similarly, , , and are terms by clause (ii) of the definition of 'term'.
Next, by clause (iii) of the definition of 'term', the following two expressions are terms.
Then, by clause (iii) of the definition of 'term', the following is a term.
Finally, (1) is a term by clause (iii) of the definition of 'term'. However, because it contains variables, it is not a name.
Example 2
[edit | edit source]We already saw that (1) is a term. Thus, by clause (ii) of the definition of formula, (2) is a formula.
Example 3
[edit | edit source]By clause (i) in the definition of 'term', , , and are terms.
By clause (ii) of the definition for 'formula', the following are formulae.
By clause (iii-d) of the definition for 'formula', the following is a formula.
By clause (iv-a) of the definition for 'formula', the following is a formula.
By clause (iii-b) of the definition for 'formula', the following is a formula.
Finally, by clause (iv-b) of the definition for 'formula', (3) is a formula.
Free and Bound Variables
[edit | edit source]Informal notions
[edit | edit source]The two English sentences,
- If Socrates is a person, then Socrates is mortal,
- if Aristotle is a person, then Aristotle is mortal,
are both true. However, outside any context supplying a reference for 'it',
- (1) If it is a person, then it is mortal,
is neither true nor false. 'It' is not a name, but rather an empty placeholder. 'It' can refer to an object by picking up its reference from the surrounding context. But without such context, there is no reference and no truth or falsity. The same applies to the variable 'x' in
- (2) If x is a person, then x is mortal.
This situation changes with the two sentences:
- (3) For any object, if it is a person, then it is mortal,
- (4) For any object x, if x is a person, then x is mortal.
Neither the occurrences of 'it' nor the occurrences of 'x' in these sentences refer to specific objects as with 'Socrates' or 'Aristotle'. But (3) and (4) are nonetheless true. (3) is true if and only if:
- (5) Replacing both occurrences of 'it' in (3) with a reference to any object whatsoever (the same object both times) yields a true result.
But (5) is true and so is (3). Similarly, (4) is true if and only if:
- (6) Replacing both occurrences of 'x' in (4) with a reference to any object whatsoever (the same object both times) yields a true result.
But (3) is true and so is (4). We can call the occurrences of 'it' in (1) free and the occurrences of 'it' in (3) bound. Indeed, the occurrences of 'it' in (3) are bound by the phrase 'for any'. Similarly, the occurrences 'x' in (2) are free while those in (4) are bound. Indeed, the occurrences of 'x' in (4) are bound by the phrase 'for any'.
Formal definitions
[edit | edit source]An occurrence of a variable is bound in if that occurrence of stands within a subformula of having one of the two forms:
Consider the formula
Both instances of are bound in (7) because they stand within the subformula
Similarly, both instances of are bound in (7) because they stand within the subformula
An occurrence of a variable is free in if and only if is not bound in . The occurrences of both and in
are free in (8) because neither is bound in (8).
We say that an occurrence of a variable is bound in by a particular occurrence of if that occurrence is also the first (and perhaps only) symbol in the shortest subformula of having the form
Consider the formula
The third and fourth occurrences of in (9) are bound by the second occurrence of in (9). However, they are not bound by the first occurrence of in (9). The occurrence of
in (9)—as well as the occurrence of (9) itself in (9)—are subformulae of (9) beginning with a quantifier. That is, both are subformula of (9) having the form
Both contain the second third and fourth occurrences of in (9). However, the occurrence of (10) in (9) is the shortest subformula of (9) that meets these conditions. That is, the occurrence of (10) in (9) is the shortest subformula of (9) that both (i) has this form and (ii) contains the third and fourth occurrences of in (9). Thus it is the second, not the first, occurrence of in (9) that binds the third and forth occurrences of in (9). The first occurrence of in (9) does, however, bind the first two occurrences of in (9).
We also say that an occurrence of a variable is bound in by a particular occurrence of if that occurrence is also the first (and perhaps only) symbol in the shortest subformula of having the form
Finally, we say that a variable (not a particular occurrence of it) is bound (or free) in a formula if the formula contains a bound (or free) occurrence of . Thus is both bound and free in
since this formula contains both bound and free occurrences of . In particular, the first two occurrences of are bound and the last is free.
Sentences and formulae
[edit | edit source]A sentence is a formula with no free variables. Sentential logic had no variables at all, so all formulae of are also sentences of . In predicate logic and its language , however, we have formulae that are not sentences. All of (7), (8), (9), and (10) above are formulae. Of these, only (7), (9), and (10) are sentences. (8) is not a sentence because it contains free variables.
Examples
[edit | edit source]All occurrences of in
are bound in the formula. The lone occurrence of is free in the formula. Hence, (11) is a formula but not a sentence.
Only the first two occurrences of in
are bound in the formula. The last occurrence of and the lone occurrence of in the formula are free in the formula. Hence, (12) is a formula but not a sentence.
All four occurrences of in
are bound. The first two are bound by the universal quantifier, the last two are bound by the existential quantifier. The lone occurrence of in the formula is free. Hence, (13) is a formula but not a sentence.
All three occurrences of in
are bound by the universal quantifier. Both occurrences of in the formula are bound by the existential quantifier. Hence, (14) has no free variables and so is a sentence and as well as a formula.
Models
[edit | edit source]Interpretations
[edit | edit source]We said earlier that the formal semantics for a formal language such as (and now ) goes in two parts.
- Rules for specifying an interpretation. An interpretation assigns semantic values to the non-logical symbols of a formal syntax. Just as a valuation was an interpretation for a sentential language, a model is an interpretation for a predicate language.
- Rules for assigning semantic values to larger expressions of the language. All formulae of the sentential language are sentences. This enabled rules for assigning truth values directly to larger formulae. For the predicate language , the situation is more complex. Not all formulae of are sentences. We will need to define the auxiliary notion satisfaction and use that when assigning truth values.
Models
[edit | edit source]A model is an interpretation for a predicate language. It consists of two parts: a domain and interpretation function. Along the way, we will progressively specify an example model .
Domain
[edit | edit source]- A domain is a non-empty set.
Intuitively, the domain contains all the objects under current consideration. It contains all of the objects over which the quantifiers range. is then interpreted as 'for any object in the domain …'; is interpreted as 'there exists at least one object in the domain such that …'. Our predicate logic requires that the domain be non-empty, i.e., that it contains at least one object.
The domain of our example model , written , is {0, 1, 2}.
Interpretation function
[edit | edit source]- An interpretation function is an assignment of semantic value to each operation letter and predicate letter.
The interpretation function for model is .
Operation letters
[edit | edit source]- To each constant symbol (i.e., zero-place operation letter) is assigned a member of the domain.
Intuitively, the constant symbol names the object, a member of the domain. If the domain is above and is assigned 0, then we think of naming 0 just as the name 'Socrates' names the man Socrates or the numeral '0' names the number 0. The assignment of 0 to can be expressed as:
- To each n-place operation letter with n greater than zero is assigned an n+1 place function taking ordered n-tuples of objects (members of the domain) as its arguments and objects (members of the domain) as its values. The function must be defined on all n-tuples of members of the domain.
Suppose the domain is above and we have a 2-place operation letter . The function assigned to must then be defined on each ordered pair from the domain. For example, it can be the function such that:
The assignment to the operation letter is written as:
Suppose that is assigned 0 as above and also that is assigned 1. Then we can intuitively think of the informally written as naming (referring to, having the value) 1. This is analogous to 'the most famous student of Socrates' naming (or referring to) Plato or '2 + 3' naming (having the value) 5.
Predicate letters
[edit | edit source]- To each sentence letter (i.e., zero-place predicate letter) is assigned a truth value. For a sentence letter, either
or
This is the same treatment sentence letters received in sentential logic. Intuitively, the sentence is true or false accordingly as the sentence letter is assigned the value 'True' or 'False'.
- To each n-place predicate letter with n greater than zero is assigned an n-place relation (a set of ordered n-tuples) of members of the domain.
Intuitively, the predicate is true of each n-tuple in the assigned set. Let the domain be above and assume the assignment
Suppose that is assigned 0, is assigned 1, and is assigned 2. Then intuitively , , and should each be true. However, , among others, should be false. This is analogous to 'is snub-nosed' being true of Socrates and 'is greater than' being true of .
Summary
[edit | edit source]The definition is interspersed with examples and so rather spread out. Here is a more compact summary. A model consists of two parts: a domain and interpretation function.
- A domain is a non-empty set.
- An interpretation function is an assignment of semantic value to each operation letter and predicate letter. This assignment proceeds as follows:
- To each constant symbol (i.e., zero-place operation letter) is assigned a member of the domain.
- To each n-place operation letter with n greater than zero is assigned an n+1 place function taking ordered n-tuples of objects (members of the domain) as its arguments and objects (members of the domain) as its values.
- To each sentence letter (i.e., zero-place predicate letter) is assigned a truth value.
- To each n-place predicate letter with n greater than zero is assigned an n-place relation (a set of ordered n-tuples) of members of the domain.
Examples
[edit | edit source]A finite model
[edit | edit source]An example model was specified in bits and pieces above. These pieces, collected together under the name , are:
We have not yet defined the rules for generating the semantic values of larger expressions. However, we can see some simple results we want that definition to achieve. A few such results have already been described:
Some more desired results can be added:
We can temporarily pretend that the numerals '0', '1', and '2' are added to and assign then the numbers 0, 1, and 2 respectively. We then want:
Because of (1), we will want as a result:
Because of (2), we will want as a result:
An infinite model
[edit | edit source]The domain had finitely many members; 3 to be exact. Domains can have infinitely many members. Below is an example model with an infinitely large domain.
The domain is the set of natural numbers:
The assignments to individual constant symbols can be as before:
The 2-place operation letter can be assigned, for example, the addition function:
The 2-place predicate letter can be assigned, for example, the less than relation:
Some results that should be produced by the specification of an extended model:
For every x, there is a y such that x < y. Thus we want as a result:
There is no y such that y < 0 (remember, we are restricting ourselves to the domain which has no number less than 0). So it is not the case that, for every x, there is a y such that y < x. Thus we want as a result:
Satisfaction
[edit | edit source]The rules for assigning truth to sentences of should say, in effect, that
is true if and only if is true of every object in the domain. There are two problems. First, can, in general, have free variables. In particular, will normally be free (otherwise saying "for all …" is irrelevant). But formulae with free variables are not sentences and do not have a truth value. Second, we do not yet have a precise way of saying that is true of every object in the domain. The solution to these problems comes in two parts:
- assignment of objects from the domain to each of the variables,
- specification of whether a model satisfies a formula with a particular assignment of variables.
We can then define truth in a model in terms of satisfaction.
Variable assignment
[edit | edit source]Given model , a variable assignment, denoted , is a function assigning a member of the domain to each variable of . For example, if contains natural numbers, then applied to variable could be .
In addition to variable assignment, we also have the assignment of domain members to constant symbols by the model's interpretation function . Together, we use this information to generate assignments of domain members to arbitrary terms (including, constant symbols, variables, and complex terms formed by operation letters acting on other terms). This is accomplished by an extended variable assignment, denoted , which is defined below. Recall that the interpretation function assigns semantic values to the operation letters and predicate letters of .
An extended variable assignment is a function that assigns a value from as follows.
- If is a variable, then:
- If is a constant symbol (i.e., a 0-place operation letter), then:
- If is an n-place operation letter (n greater than 0) and are terms, then:
Some examples may help. Suppose we have model where:
On the previous page, it was noted that we want the following result:
We now have achieved this because we have for any defined on :
Suppose we also have a variable assignment where:
Then we get:
Satisfaction
[edit | edit source]A model, together with a variable assignment, can satisfy (or fail to satisfy) a formula. Then we will use the notion of satisfaction with a variable assignment to define truth of a sentence in a model. We can use the following convenient notation to say that the interpretation satisfies (or does not satisfy) with .
We now define satisfaction of a formula by a model with a variable assignment. In the following, 'iff' is used to mean 'if and only if'.
-
- .
-
- .
Examples
[edit | edit source]The following continue the examples used when describing extended variable assignments above. They are based on the examples of the previous page.
A model and variable assignment for examples
[edit | edit source]Suppose we have model where
Suppose further we have a variable assignment where:
We already saw that both of the following resolve to 1:
Examples without quantifiers
[edit | edit source]Given model , the previous page noted the following further goals:
We are not yet ready to evaluate for truth or falsity, but we can take a step in that direction by seeing that these sentences are satisfied by with Indeed, the details of will not figure in determining which of these are satisfied. Thus satisfies (or fails to satisfy) them with any variable assignment. As we will see on the next page, that is the criterion for truth (or falsity) in .
Corresponding to (1),
In particular:
Corresponding to (2) through (6) respectively:
As noted above, the details of were not relevant to these evaluations. But for similar formulae using free variables instead of constant symbols, the details or do become relevant. Examples based the above are:
Examples with quantifiers
[edit | edit source]Given model , the previous page also noted the following further goals:
Again, we are not yet ready to evaluate for truth or falsity, but again we can take a step in that direction by seeing that the sentence in (7) is and the sentence in (8) is not satisfied by with
Corresponding to (7):
is true if and only if at least one of the following is true:
The formula of (7) and (9) is satisfied by if and only if it is satisfied by with each of the modified variable assignments. Turn this around, and we get the formula failing to be satisfied by if and only if it fails to be satisfied by the model with at least one of the three modified variable assignments as per (10) through (12). Similarly, (10) is true if and only if at least one of the following are true:
Indeed, the middle one of these is true. This is because
Thus (9) is true.
Corresponding to (8),
is true if and only if at least one of the following is true:
The middle of these is true if and only if at least one of the following are true:
Indeed, the last of these is true. This is because:
Thus (13) is true.
Truth
[edit | edit source]Truth in a model
[edit | edit source]We have defined satisfaction in a model with a variable assignment. We have expressed formula being satisfied by model with variable assignment as
Now we can also say that a formula is satisfied by model (not limited to a specific variable assignment) if is satisfied by with every variable assignment. Thus
if and only if
If no free variables occur in (that is, if is a sentence), then is true in model .
Variable assignments allow us to deal with free variables when doing the semantic analysis of a formula. For two variable assignments, and , satisfaction by differs from satisfaction by only if the formula has free variables. But sentences do not have free variables. Thus a model satisfies a sentence with at least one variable assignment if and only if it satisfies the sentence with every variable assignment. The following two definitions are equivalent:
- A sentence is true in if and only if there is a variable assignment such that
- A sentence is true in if and only if, for every variable assignment
The latter is just a notational variant of:
- A sentence is true in if and only if
Examples
[edit | edit source]A finite model
[edit | edit source]The example model
[edit | edit source]On the previous page, we looked at the following model and variable assignment.
For the model
For the variable assignment
Example results
[edit | edit source]We noted the following results:
We also noted above that for sentences (though not for formulae in general), a model satisfies the sentence with at least one variable assignment if and only if it satisfies the sentence with every variable assignment. Thus the results just listed hold for every variable assignment, not just .
Applying our definition of truth, we get:
This corresponds to the goals (1)–(8) of the previous page. We have now achieved those goals.
An infinite model
[edit | edit source]The example model
[edit | edit source]On Models page, we also considered an infinite model
We can reuse the same variable assignment from above, namely
Example of extended variable assignment
[edit | edit source]On the Models page, we listed the following goals for our definitions.
This does not require our definition of truth or the definition of satisfaction; it is simply requires evaluating the exended variable assignment. We have for any on defined on :
Example results without quantifiers
[edit | edit source]We also listed the following goal on the Models page.
First we note that:
Indeed:
Because the formulae of (9) and (10) are sentences,
Applying the definition of truth, we find the goals of (9) and (10) achieved. The sentences of (9) are true and those of (10) are false.
Example results with quantifiers
[edit | edit source]In addition, we listed the following goal on the Models page.
Corresponding to (11):
is true if and only if, for each i a member of the domain, the following is true of at least one j a member of the domain:
But was assigned the less then relation. Thus the preceding holds if and only if, for every member of the domain, there is a larger member of the domain. Given that the domain is this is obviously true. Thus, (13) is true. Given that the formula of (11) and (12) is a sentence, we find the goal expressed as (11) to be met.
Corresponding to (12):
is true if and only if, for each i a member of the domain, the following is true of at least one j a member of the domain:
This holds if and only if, for every member of the domain, there is a smaller member of the domain. But there is no member of the domain smaller than 0. Thus (14) is false. The formula of (12) and (14) fails to be satisfied by with variable assignment . The formula of (12) and (14) is a sentence, so it fails to be satisfied by with any variable assignment. The formula (a sentence) of (12) and (14) is false, and so the goal of (12) is met.




















































































































































![{\displaystyle {\mathfrak {v}}[\mathrm {P_{0}} ]\ =\ {\mbox{True}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebced4e093fec5549c19e71009bbfe61150bcb32)
![{\displaystyle {\mathfrak {v}}[\mathrm {P_{1}} ]\ =\ {\mbox{False}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3abfe7bf710089ee4a80f78e285d70c5e2ac288)
![{\displaystyle {\mathfrak {v}}[\mathrm {P_{2}} ]\ =\ {\mbox{False}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/421c4ef2a1afc19e7f41c997a4c24a8d16ae5df1)
![{\displaystyle {\mathfrak {v}}[\mathrm {P_{3}} ]\ =\ {\mbox{False}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d825606df7242317bd0a3a3ded2cde67c2c0e41b)




![{\displaystyle {\mbox{i.}}\quad {\overline {\mathfrak {v}}}[\varphi ]={\mathfrak {v}}[\varphi ].\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5501c945370a112d0e38c8d7c98fbd1957a0b2fd)
![{\displaystyle {\mbox{ii.}}\quad {\overline {\mathfrak {v}}}[\lnot \varphi ]\ =\ {\begin{cases}{\mbox{True}}&{\mbox{if}}\ {\overline {\mathfrak {v}}}[\varphi ]={\mbox{False}};\\{\mbox{False}}&{\mbox{otherwise (i.e., if}}\ {\overline {\mathfrak {v}}}[\varphi ]={\mbox{True).}}\end{cases}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d273839318730f629b864f7ee2b347b77a3d6d18)
![{\displaystyle {\mbox{iii.}}\quad {\overline {\mathfrak {v}}}[(\varphi \land \psi )]\ =\ {\begin{cases}{\mbox{True}}&{\mbox{if}}\ {\overline {\mathfrak {v}}}[\varphi ]={\overline {\mathfrak {v}}}[\psi ]={\mbox{True}};\\{\mbox{False}}&{\mbox{otherwise}}.\end{cases}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/beee36cb5bd2db11eba8ff28102b09ab55455d54)
![{\displaystyle {\mbox{iv.}}\quad {\overline {\mathfrak {v}}}[(\varphi \lor \psi )]\ =\ {\begin{cases}{\mbox{True}}&{\mbox{if}}\ {\overline {\mathfrak {v}}}[\varphi ]={\mbox{True}}\ {\mbox{or}}\ {\overline {\mathfrak {v}}}[\psi ]={\mbox{True}}\ {\mbox{(or both)}};\\{\mbox{False}}&{\mbox{otherwise}}.\end{cases}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f77ad1978590950a29bfe27fb9eb4961336aba1e)
![{\displaystyle {\mbox{v.}}\quad {\overline {\mathfrak {v}}}[(\varphi \rightarrow \psi )]\ =\ {\begin{cases}{\mbox{True}}&{\mbox{if}}\ {\overline {\mathfrak {v}}}[\varphi ]={\mbox{False}}\ \ {\mbox{or}}\ \ {\overline {\mathfrak {v}}}[\psi ]={\mbox{True}}\ \ {\mbox{(or both)}};\\{\mbox{False}}&{\mbox{otherwise.}}\end{cases}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58609bb31fc2cf95154d2548c4186fc7b3222a83)
![{\displaystyle {\mbox{vi.}}\quad {\overline {\mathfrak {v}}}[(\varphi \leftrightarrow \psi )]\ =\ {\begin{cases}{\mbox{True}}&{\mbox{if}}\ {\overline {\mathfrak {v}}}[\varphi ]={\overline {\mathfrak {v}}}[\psi ];\\{\mbox{False}}&{\mbox{otherwise}}.\end{cases}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c7992cb4fd370092b7de8c79b88af3968e0ec08)




![{\displaystyle {\overline {\mathfrak {v}}}[\mathrm {P} ]\ =\ {\mbox{True}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78cdb69761b884faa72b30db3cff8fc4a327856f)
![{\displaystyle {\overline {\mathfrak {v}}}[\mathrm {Q} ]\ =\ {\mbox{True}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d0efa7a915fac7ef962d0f2f6ccb28929c35307)
![{\displaystyle {\overline {\mathfrak {v}}}[\mathrm {R} ]\ =\ {\mbox{False}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec51568f30e8f378d378aff08b4e904288acc51c)
![{\displaystyle {\overline {\mathfrak {v}}}[\mathrm {P} \land \mathrm {Q} ]\ =\ {\mbox{True}}.\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11cae0180cab0f6442791354b034e77a9fb6aebb)
![{\displaystyle {\overline {\mathfrak {v}}}[\mathrm {Q} \lor \mathrm {R} ]\ =\ {\mbox{True}}.\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a210367b901f58d46e5dc0bfa02614aed0e4a5cf)
![{\displaystyle {\overline {\mathfrak {v}}}[\lnot (\mathrm {Q} \lor \mathrm {R} )]\ =\ {\mbox{False}}.\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16c3679ea35b0aaa6a8d6f46967b89f9d120ef0b)
![{\displaystyle {\overline {\mathfrak {v}}}[\mathrm {P} \land \mathrm {Q} \rightarrow \lnot (\mathrm {Q} \lor \mathrm {R} )]\ =\ {\mbox{False}}.\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/254c7028855c2601b10b61357fa0c82fb832fae6)


![{\displaystyle {\overline {\mathfrak {v}}}[\mathrm {Q} ]\ =\ {\mbox{False}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcb1a4a71fc929b4b5978178306540fac36eefe8)
![{\displaystyle {\overline {\mathfrak {v}}}[\mathrm {R} ]\ =\ {\mbox{True}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1abbcf46ce1162c387f473031daa2f15c5f4be6)
![{\displaystyle {\overline {\mathfrak {v}}}[\mathrm {P} \land \mathrm {Q} ]\ =\ {\mbox{False}}.\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7537741c53cf4db9db28ae3f3938c7dae033f2e)
![{\displaystyle {\overline {\mathfrak {v}}}[\mathrm {P} \land \mathrm {Q} \rightarrow \lnot (\mathrm {Q} \lor \mathrm {R} )]\ =\ {\mbox{True}}.\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb0856841a0bf2fec31c009819a0109c99900644)
![{\displaystyle {\mathfrak {v}}[\mathrm {P} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1f290d5e2a6545283f453fc40d450f3c912e081)
![{\displaystyle {\overline {\mathfrak {v}}}[\lnot \mathrm {P} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b65176a279dec339d693de7e05a52411907cf87a)


































































![{\displaystyle {\mathfrak {v}}[(\varphi \mid \psi )]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2373a724763dbb02fd1322fd9d7a2f14a1633b9)







![{\displaystyle {\mathfrak {v}}[(\varphi \downarrow \psi )]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/832d14657b0129129e58f18ae7512a641f7debf8)







































































![{\displaystyle \varphi [\pi /\psi ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2eebfcef8dc9c38d2c05d12e2f5f0a0e35616de)


![{\displaystyle \mathrm {Q} \rightarrow (\mathrm {P} \rightarrow \mathrm {Q} )[\mathrm {Q} /\mathrm {R} \land \mathrm {S} ][\mathrm {P} /\mathrm {P} \lor \mathrm {Q} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81271051059723595e8d452d27da89f1af994693)




![{\displaystyle \mathrm {Q} \rightarrow (\mathrm {P} \rightarrow \mathrm {Q} )[\mathrm {P} /\mathrm {R} ][\mathrm {Q} /\mathrm {P} ][\mathrm {R} /\mathrm {Q} ]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a6dac03fc4768317ce9e57ee664b4a38cd4dfcf)




![{\displaystyle \varphi [\pi _{1}/\psi _{1},\ \pi _{2}/\psi _{2},\ ...]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97abe1a722c3e0bec01154fbe24631634c4e7ecf)
![{\displaystyle \mathrm {Q} \rightarrow (\mathrm {P} \rightarrow \mathrm {Q} )[\mathrm {P} /\mathrm {P} \lor \mathrm {Q} ,\mathrm {Q} /\mathrm {R} \land \mathrm {S} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86e6d375945f1499a1f619e0362ac3cb4bec2b09)
![{\displaystyle \mathrm {Q} \rightarrow (\mathrm {P} \rightarrow \mathrm {Q} )[\mathrm {P} /\mathrm {Q} ,\ \mathrm {Q} /\mathrm {P} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e422947c6c27eebd07aa0cf66ed74321e18f1561)
![{\displaystyle \mathrm {Q} \rightarrow (\mathrm {P} \rightarrow \mathrm {Q} )[\mathrm {Q} /\mathrm {P} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfca8b9e7c07ffb3fd96e9180eda01663234be6f)










































































![{\displaystyle [\mathrm {P} \lor \mathrm {Q} \rightarrow \lnot \mathrm {R} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa44596d60b688c05bbdbe0bc7247ed056fb546a)



![{\displaystyle [\mathrm {P} \rightarrow \lnot \mathrm {R} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94b1bf4e357c16d14c5edd2c38d2d82c0bcf02ac)
![{\displaystyle [\lnot \mathrm {R} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8b390160716315f88a8ad089d9a9d61428354ee)


![{\displaystyle [\mathrm {Q} \rightarrow \lnot \mathrm {R} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e985539e01255392f5c1c6fe670de638714a63f8)


![{\displaystyle [\mathrm {P} \rightarrow \mathrm {P} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79933dc3c8b22ad47c5f28386ff6e8976b768d5e)

![{\displaystyle [\mathrm {Q} \rightarrow (\mathrm {P} \rightarrow \mathrm {Q} )]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94b8be83a1ab88d731a8b904852f116034ad2939)
![{\displaystyle [\mathrm {P} \rightarrow \mathrm {Q} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97cf4af3c1bca8188faa85c99bb829c88690a523)

![{\displaystyle [\mathrm {Q} \rightarrow \mathrm {Q} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3c0af0222220bbc7f981fe3c5a3d969cb2fd7a9)








![{\displaystyle [\mathrm {P} \rightarrow \lnot \lnot \mathrm {P} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a010f77ae19f9aea6fabf12869899e6216e77bc)
![{\displaystyle [\lnot \lnot \mathrm {P} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d56c2499de3ac67a73cdcaca427dce5605b4320b)




![{\displaystyle [\lnot \lnot \mathrm {P} \rightarrow \mathrm {P} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1bb69f44806a433fd72926eb47f9b4ffa7a043c)
![{\displaystyle [\mathrm {P} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81936377579d3940eeb3983f919467358a9f12aa)



![{\displaystyle [\mathrm {P} \land \lnot \mathrm {P} \rightarrow \mathrm {Q} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/218e914cb2dfec118a310f2d3b6de200ee6e08d2)
![{\displaystyle [\mathrm {Q} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b99e6e42dce9a0938a5354e1018054a02fca2ad3)



![{\displaystyle [\lnot \mathrm {P} \rightarrow (\mathrm {P} \rightarrow \mathrm {Q} )]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de406ff15ac87549e0b995a4fa7d7e4dc2b2fea1)




![{\displaystyle [(\mathrm {P} \rightarrow \mathrm {Q} )\land \lnot \mathrm {Q} \rightarrow \lnot \mathrm {P} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/822876910ec839e4e6294e59bb10a63c5aa3d174)
![{\displaystyle [\lnot \mathrm {P} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebecf005a1793b292d92ddec0a677c0612909c89)
















![{\displaystyle [(\mathrm {P} \lor \mathrm {Q} )\land \lnot \mathrm {P} \rightarrow \mathrm {Q} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce2fd880e79bd95061a9001884c5f98b39d25c94)



![{\displaystyle [(\mathrm {P} \lor \mathrm {Q} )\land \lnot \mathrm {Q} \rightarrow \mathrm {P} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/017310eff4f2d7cae3bd6dd40e51e5acc578175e)




![{\displaystyle [(\lnot \mathrm {P} \rightarrow \mathrm {Q} )\rightarrow \mathrm {P} \lor \mathrm {Q} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d274e3f04d76311583944ef8236ff241af80cfab)
![{\displaystyle [\mathrm {P} \lor \mathrm {Q} ]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d908c75773c25f4ce62e273bd9b6b7abe190692f)

![{\displaystyle [\lnot (\mathrm {P} \rightarrow \mathrm {Q} )\rightarrow (\mathrm {Q} \rightarrow \mathrm {R} )]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f17aa6df957ee3265b637942af874d9ab1c05c8)
































































































































































































































![{\displaystyle \langle {\mathfrak {M}},\ \mathrm {s} \rangle \ \vDash \forall \alpha \,\varphi \quad {\mbox{iff}}\ \ {\mbox{for every}}\ \mathrm {d} \ \in |{\mathfrak {M}}|,\ \langle {\mathfrak {M}},\ \mathrm {s[\alpha \!:\,d]} \rangle \ \vDash \varphi \ .\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7c631086d8f9f7cbec2219483df94a0bfd1ae69)
![{\displaystyle {\mbox{where}}\ \mathrm {s[\alpha \!:\,d]} \ {\mbox{differs from}}\ \mathrm {s} \ {\mbox{only in assigning}}\ \mathrm {d} \ {\mbox{to}}\ \alpha \ .\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/278c5e13beb24fdd1720e8b84b76c91d536f1f9a)

![{\displaystyle \langle {\mathfrak {M}},\ \mathrm {s} \rangle \ \vDash \exists \alpha \,\varphi \quad {\mbox{iff}}\ \ {\mbox{for at least one}}\ \mathrm {d} \in |{\mathfrak {M}}|,\ \langle {\mathfrak {M}},\ \mathrm {s[\alpha \!:\,d]} \rangle \ \vDash \varphi \ .\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28adc8a563598602446e758b3dd8178a1f6ddda8)































![{\displaystyle (10)\quad \langle {\mathfrak {M}},\ \mathrm {s} [x\!:\,0]\rangle \ \not \vDash \forall y\,(\mathrm {F} (x,y)\rightarrow \mathrm {F} (y,x))\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/248790c7c4850042ed0d3adb40f3df5f674beee6)
![{\displaystyle (11)\quad \langle {\mathfrak {M}},\ \mathrm {s} [x\!:\,1]\rangle \ \not \vDash \forall y\,(\mathrm {F} (x,y)\rightarrow \mathrm {F} (y,x))\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78bef17e267c5461e9856197d59be3015aa467ea)
![{\displaystyle (12)\quad \langle {\mathfrak {M}},\ \mathrm {s} [x\!:\,2]\rangle \ \not \vDash \forall y\,(\mathrm {F} (x,y)\rightarrow \mathrm {F} (y,x))\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f1148d28e89d73cc5236b60e83e0d0e732bc911)

![{\displaystyle \langle {\mathfrak {M}},\ \mathrm {s} [x\!:\,0,\ y\!:\,0]\rangle \ \not \vDash \mathrm {F} (x,y)\rightarrow \mathrm {F} (y,x)\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f55e18b1a792cf431ebd038d24296711e6ac0952)
![{\displaystyle \langle {\mathfrak {M}},\ \mathrm {s} [x\!:\,0,\ y\!:\,1]\rangle \ \not \vDash \mathrm {F} (x,y)\rightarrow \mathrm {F} (y,x)\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df7ad3f9d46f3f1b942d0c14a61bcff4adf517b8)
![{\displaystyle \langle {\mathfrak {M}},\ \mathrm {s} [x\!:\,0,\ y\!:\,2]\rangle \ \not \vDash \mathrm {F} (x,y)\rightarrow \mathrm {F} (y,x)\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb8b6ee8001f5cf1b08f912b78e9e75022cdc61d)


![{\displaystyle \langle {\mathfrak {M}},\ \mathrm {s} [x\!:\,0]\rangle \ \vDash \exists y\,(\mathrm {F} (x,y)\land \mathrm {F} (y,x))\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33a6b8e1209d24aea00d5d54f5371da896c4ed47)
![{\displaystyle \langle {\mathfrak {M}},\ \mathrm {s} [x\!:\,1]\rangle \ \vDash \exists y\,(\mathrm {F} (x,y)\land \mathrm {F} (y,x))\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8f97201239b90a398d7eab7e51c0a444efc3cb1)
![{\displaystyle \langle {\mathfrak {M}},\ \mathrm {s} [x\!:\,2]\rangle \ \vDash \exists y\,(\mathrm {F} (x,y)\land \mathrm {F} (y,x))\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34b4256bdc13fc42a5e5d1c3131a41704e4c816b)
![{\displaystyle \langle {\mathfrak {M}},\ \mathrm {s} [x\!:\,1,\ y\!:\,0]\rangle \ \vDash \mathrm {F} (x,y)\land \mathrm {F} (y,x)\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71c9eca8553a860f592cd8781a40119e1281e83c)
![{\displaystyle \langle {\mathfrak {M}},\ \mathrm {s} [x\!:\,1,\ y\!:\,1]\rangle \ \vDash \mathrm {F} (x,y)\land \mathrm {F} (y,x)\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32b6b5c86f378fe24d53965bb8b46e189779fcb3)
![{\displaystyle \langle {\mathfrak {M}},\ \mathrm {s} [x\!:\,1,\ y\!:\,2]\rangle \ \vDash \mathrm {F} (x,y)\land \mathrm {F} (y,x)\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82ee4fd3652bf7712775ca65075f3fb82157b0fb)








































![{\displaystyle \langle {\mathfrak {M_{2}}},\ \mathrm {s} [x\!:\,i,x\!:\,j]\rangle \ \vDash \mathrm {F} (x,y)\ .\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5227c573961f96feaf1fa53da99e0cfddcd15ef5)


![{\displaystyle \langle {\mathfrak {M_{2}}},\ \mathrm {s} [x\!:\,i,x\!:\,j]\rangle \ \vDash \mathrm {F} (y,x)\ .\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fd7b5df0184d3bb056f21c64b08f37a8f72ebbf)
