FHSST Physics/Atomic Nucleus/Quarks and Leptons
Quarks and Leptons
[edit | edit source]While experimentalists seemed to be lost in the maze, the theoreticians groped for the way out. Using an extremely complicated mathematical technique, they managed to group the hadrons in such families which implied that all known (and yet unknown) hadrons are built of only six types of particles with fractional charges. The main credit for this (in the form of Nobel Prize) was given to M. Gell-Mann and G. Zweig.
At first, they considered a subset of the hadrons and developed a theory with only three types of such truly elementary particles. When Murray Gell-Mann thought of the name for them, he came across the book "Finnegans Wake" by James Joyce. The line "Three quarks for Muster Mark!" appeared on page 383 of that book (the word quark there is a merging of the words quart and quack, among others). He needed a name for three particles and this was the answer. Thus the term quark was coined.
Later, the theory was generalized to include all known particles, which required six types of quarks. Modern theories require also that the number of different leptons should be the same as the number of different quark types. According to these theories, the quarks and leptons are truly elementary, i.e. they do not have any internal structure and therefore are of a zero size (pointlike). Thus, the world is constructed of just twelve types of elementary building blocks that are given in Table 15.4. Amazingly enough, the electron that was discovered before all other particles, more than a century ago, turned out to be one of them!
| family | elementary particle | symbol | charge | lepton number | baryon number | mass (MeV) |
|---|---|---|---|---|---|---|
| electron | 1 | 0 | 0.511 | |||
| muon | 1 | 0 | 105.7 | |||
| leptons | tau | 1 | 0 | 1777 | ||
| electron neutrino | 1 | 0 | ||||
| muon neutrino | 1 | 0 | ||||
| tau neutrino | 1 | 0 | ||||
| up | 0 | 1/3 | 360 | |||
| down | 0 | 1/3 | 360 | |||
| quarks | strange | 0 | 1/3 | 1500 | ||
| charmed | 0 | 1/3 | 540 | |||
| top (truth) | 0 | 1/3 | 174000 | |||
| bottom (beauty) | 0 | 1/3 | 5000 |
After Gell-Mann, who used a funny name (quark) for an elementary particle, the fundamental physics was flooded with such names. For example, the six quark types are called flavors (for cottage cheese, this is appropriate indeed), the three different states in which each quark can be, are called colors (red, green, blue) etc. Modern physics is so complicated and mathematical, that people working in it, need such kind of jokes to spice unsavoury dish with flavors. The funny names should not confuse anybody. Elementary particles do not have any smell, taste, or colour. These terms simply denote certain properties (similar to electric charge) that do not exist in human world.
Hadrons
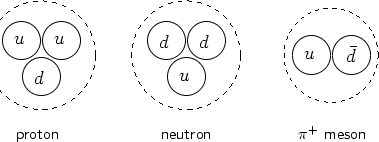
[edit | edit source]There are particles that are able to interact with each other by the so-called strong forces. Another name for these forces is nuclear forces. They are very strong at short distances (m), and very quickly vanish when the distance between the particles increases. All these particles are called hadrons. The protons and neutrons are examples of hadrons. As you remember, we learned about the existence of huge variety of particles when trying to look inside a nucleon, more particularly, the neutron. So, what the neutron is made of? Can we get the answer at last, after learning about the quarks? Yes, we can. According to modern theories, all hadrons are composed of quarks. The quarks can be combined in groups of two or three. The boundstates of two quarks are called mesons, and the boundcomplexes of three quarks are called baryons. No other numbers of quarks can form observable particles (Recently, experimentalists and theoreticians started to actively discuss the possibility of the existence of pentaquarks, exotic particles that are bound complexes of five quarks.).
Nucleons are baryons and therefore consist of three quarks while the pion is a meson containing only two quarks, as schematically shown in Fig. 15.7. Comparing this figure with Table 15.4, you can see why quarks have fractional charges. Counting the total charge of a hadron, you should not forget that anti-quarks have the opposite charges. The baryon number for an anti-quark also has the opposite sign (negative). This is why mesons actually consist of a quark and anti-quark in order to have total baryon number zero.
Particle reactions
[edit | edit source]At the early stages of the particle physics development, in order to find the constituent parts of various particles, experimentalists simply collided them and watched the fragments. However, this straightforward approach led to confusion. For example, the reaction between the meson and proton,
|
(15.8) |
would suggest (if naively interpreted) that either or is a constituent part of the nucleon while the pion is incorporated into the other fragment. On the other hand, the same collision can knock out different fragments from the same proton. For example,
|
(15.9) |
which leads to an absurd suggestion that neutron is a constituent part of proton.
The quark model explains all such puzzles nicely and logically. Similarly to chemical reactions that are just rearrangements of atoms, the particle reactions of the type (15.8 and 15.9) are just rearrangements of the quarks. The only difference is that, in contrast to chemistry where the number of atoms is not changing, the number of quarks before the collision is not necessarily equal to their number after the collision. This is because a quark from one colliding particle can annihilate with the corresponding antiquark from another particle. Moreover, if the collision is sufficiently powerful, the quark-antiquark pairs can be created from vacuum.
It is convenient to depict the particle transformations in the form of the so-called quark flow diagrams. On such diagrams, the quarks are represented by lines that may be visualized as the trajectories showing their movement from the left to the right.

|
For example, the diagram given in Fig. 15.8, shows the quark rearrangement for the reaction (15.8). As you can see, when the pion collides with proton, its quark annihilates with the quark from the proton. At the same time, the pair is created from the vacuum. Then, the quark binds with the quark to form the strange meson , while the quark goes together with the pair as the strange baryon .

|
The charge-exchange reaction (15.9) is a more simple rearrangement process shown in Fig. 15.9. You may wonder why the quark and antiquark of the same flavor in the meson do not annihilate. Yes they do, but not immediately. And due to this annihilation, the lifetime of is 100 million times shorter than the lifetime of (see Table 15.3).
Despite its simplicity, the quark-flow diagram technique is very powerful method not only for explaining the observed reactions but also for predicting new reactions that have not yet been seen in experiments. Knowing the quark content of particles (which is available in modern Physics Handbooks), you can draw plenty of such diagrams that will describe possible particle transformations. The only rule is to keep the lines continuous. They can disappear or emerge only for a quark-antiquark pair of the same flavor.
However, the continuity of the quark lines is valid only for the processes caused by the strong interaction. Indeed, the -decay of a free neutron (caused by the weak forces),
| (15.10) |
as well as the -decay of the nuclei, indicate that quarks can change flavor. In particular, the -decay (15.10 or 15.6) happens because the quark transformes into the quark,
| (15.11) |
due to the weak interaction, as shown in Fig. 15.10

|
Quark confinement
[edit | edit source]At this point, it is very logical to ask if anybody observed an isolated quark. The answer is no. Why? And how can one be so confident of the quark model when no one has ever seen an isolated quark?
Basically, you can't see an isolated quark because the quark-quark attractive force does not let them go. In contrast to all other systems, the attraction between quarks grows with the distance separating them. It is like a rubber cord connecting two balls. When the balls are close to each other, the cord is not stretched and the balls do not feel any force. If, however, you try to separate the balls, the cord pulls them back. The more you stretch the cord, the stronger the force becomes (according to the Hook's law of elasticity). Of course, a real rubber cord would eventually break. This does not happen with the quark-quark force. It can grow to infinity. This phenomenon is called the confinement of quarks.
Nonetheless, we are sure that the nucleon consists of three quarks having fractional charges. A hundred years ago Rutherford, by observing the scattering of charged particles from an atom, proved that its positive charge is concentrated in a small nucleus. Nowadays, similar experiments prove the existence of fractional point-like charges inside the nucleon.
The quark model actually is much more complicated than the quark-flow diagrams. It is a consistent mathematical theory that explains a vast variety of experimental data. This is why nobody doubts that it reflects the reality.