Engineering Acoustics/Qualitative Description of Shocks
Defining a Shock-Wave
[edit | edit source]In the general case of mechanical wave propagation it is assumed that the intensive properties of the medium can be described by continuous functions of space and time. In the limit where pressure amplitudes become very large, the wave propagation can evolve such that the wave front becomes discontinuous and must be described in terms of a jump from the undisturbed thermodynamic states in front of the wave to the final thermodynamic states behind the wave.
A propagating disturbance of this type, which generates a discontinuous change in pressure, temperature, enthalpy, internal energy, density and particle velocity is referred to as a shock wave. A shock-wave is depicted schematically in the following figure:

A shock-wave can ultimately be interpreted as a transverse mechanical wave with an undefinable pulse wavelength that discontinuously changes the state of the medium at a propagation velocity greatly exceeding the sound speed of the medium.
Shock Formation and Attenuation
[edit | edit source]"Shocking Up"
[edit | edit source]It is most intuitive to consider how a shock wave is formed by considering the process in an elastic solid as the behaviour can then be extended in principle to fluids. For a linear-elastic material, behaviour under compressive loading can be broadly described by two regimes. In the elastic regime the deformation (strain) is directly proportional to the stress applied to it. Above a certain critical stress level (termed the yield stress) the strain is no longer directly proportional to the stress and the material begins to behave nonlinearly - this is the plastic regime.
If we define the sound speed in the material as:
It is clear that in the elastic regime pressure and density are linearly related and thus the speed of propagation of a wave is constant if their pressure amplitudes are below the yield stress of the material. However, consider a wave whose amplitude is in the regime of pressure beyond the yield strength as depicted in the following figure:

Since the pressure amplitudes are past the regime of linear proportionality between stress and strain the wave speed is no longer constant. By consulting the stress-strain curve it is apparent that wave velocity increases with increasing pressure beyond the elastic limit. Consequently, point C of the waveform will have the lowest local wave speed while points B and A will have consecutively increasing wave speeds. As a result the highest pressure parts of the waveform travel faster than the lower parts and must eventually overtake them. A time lapse of this process is depicted as follows:

As the smooth wave pulse propagates through the material the instantaneously faster parts of the wave overtake the slower ones and the pulse itself becomes increasingly steep until it adopts the familiar, discontinuous profile associated with a shock-wave. Consequently any wave with pressure amplitudes greater than the yield strength of the material will eventually "shock-up" and become discontinuous due to the non-linear increase in wave speed with increasing pressure.
It is tempting to assume that if we were to play the evolution of the shock-wave even further in time, the top of the vertical line would continue to outpace the bottom and the shock wave front would become sloped. This does not happen in reality due to a competing wave process that serves to attenuate the shock.
Shock Rarefaction
[edit | edit source]Once a shock-wave has established itself in a material it cannot propagate indefinitely unless it is either driven mechanically via a piston or self supported via coupled chemical reaction in a detonation wave. It will be shown that the attenuation and eventual dissipation of a shock wave is also the natural result of the non-linear relation between pressure, density and wave speed above the elastic limit.
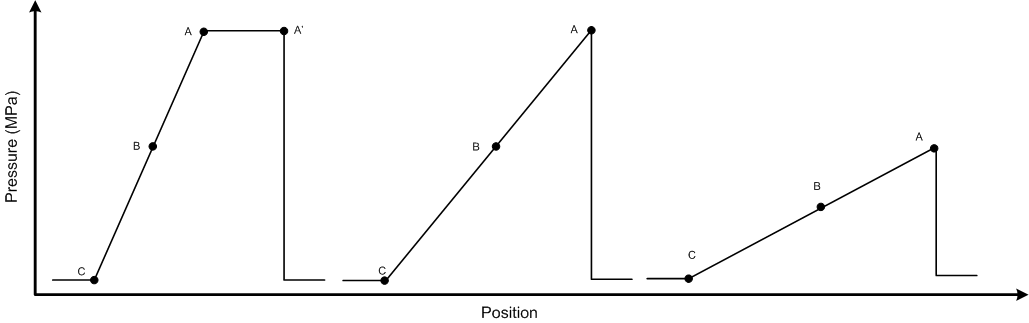
Consider the following square pulse shock wave:

Examine point A': It is moving into un-shocked material with wave speed and associated particle speed . In contrast, point A is moving into already shocked material at significantly higher pressure and density and thus with higher particle velocity, and wave speeds . Consequently, point A will be moving significantly faster than point A' and will soon overtake the front. Now examine point C. It has been relieved down to ambient conditions and thus has a low associated wave speed. It will thus lag progressively further and further behind point A. As the shock-wave wave propagates, the line A-C will stretch out and thus angle down. This can be see as an averaging out of the shock pulse amplitude over a larger and large front thickness. This averaging serves to attenuate the pulse until the pressure decays below the elastic limit and the shock-wave devolves into an acoustic wave. The line A-C is in fact a wave process with a propagation velocity faster than that of the shock front. Such a wave is known as a rarefaction and it is a fundamental characteristic of shock-wave processes. The rarefaction attenuation process is depicted in the following figure:
Shock Description via the Method of Characteristics
[edit | edit source]While the previous discussion is extremely intuitive in understanding shock behaviour, all of these results can be obtained directly via mathematical solution of the non-linear wave equations through the method of characteristics and Riemann Invariants. The method of characteristics is a technique for solving partial differential equations by reducing the PDE to a set of ordinary differential equations through the parametrization of the existing coordinate system into a new system where properties of the PDE remain constant over curves in the new system. The contours revealed during this method are called characteristics.
Consider the basic set of nonlinear-elastic wave equations:
- strain-density relation
- constitutive equation
- conservation of mass
- conservation of momentum
And characteristic coordinates:
Subject to the constraints where :
Where we define:
Note that here we have effectively employed the expression for wave speed as a function of pressure and density!
Yielding the constraint equations:
Combining the constraint equations with the differentials and yields :
These equations then yield the slopes of the contours of the new coordinate system:
- when
- when
We must now apply these relations to transform the expression of the wave equations from space into space. Take the time derivative of constitutive equation and substitute the slope of the characteristic lines to obtain:
For simplicity make the substitution
Substitution into the conservation of mass and momentum equations yields:
These can be combined and solved via partial derivative chain rule expansion to yield:
These are the characteristic equations in and space.
In order to solve for the characteristic contours we must integrate from some reference to a final state with reference to the invariants, thus:
These two equations represent the Riemann invariants for the wave system. They can be combined to yield the characteristic equations for which the combination of stress and particle velocity does not change as follows:
Simple Wave Solution
[edit | edit source]A simple wave is a solution to the wave equations in characteristic space for which one of the invariants is constant. Consider a non-linear wave where we set:
This yields stress, strain, particle velocity, and sound speeds that are solely a function of . From the slopes of the coordinate contours derived previously we obtain:
Integration of these contours directly yields :
Consequently the simple wave solution of the non linear equations in characteristic space can described as a transformation of a specified transversely moving pulse into a collection of straight line characteristics with differing slopes. Each line can be interpreted as the x-t history of one specific point on the pulse.
If we compute the Riemann integrals:
We obtain the important result:
This inequality mathematically substantiates our previous statement that wave speed increases with increasing pressure in the non-linear (plastic) regime and illustrates an important concept: the wave speed is equal to the sum of the particle velocity and the sound speed.
The relation between simple wave solutions in characteristic space can be linked to the formation of shock waves through the concept that characteristics with varying slopes must eventually intersect at some point in time.
Shocks From Waves
[edit | edit source]It can be shown mathematically that the point of intersection of the contours of a non-linear wave is a mathematical discontinuity, thereby recovering our concept that shock-waves are state discontinuities
For simplicity sake consider a wave that is a ramp of particle velocity with respect to position - this is analogous our previous qualitative example from the first section but with particle velocity plotted instead of pressure (where the two are related). The equation describing this ramp is:
Applying our solution for the characteristics of a simple wave we obtain:
In order to make this solution tractable we must employ an equation of state to mathematically link the wave velocity and particle speeds. Since we have not specified the material in question it is expedient to simply assume that the relationship is linear, thus:
Substituting this into our relationship we obtain for velocity:
Clearly when , the value for the particle velocity is undefined and the simple wave solution breaks down and we have a shock-wave formed. However, when is negative, the value of never tends to infinity and we have a rarefaction wave. If we plot the position history of one point at the bottom of the ramp (corresponding to the point C in our previous discussion) and one point at the top of our ramp (corresponding to point A) on an x-t diagram we can visualize how these characteristics behave:

It is important to note that our mathematical and conceptual discussions have ultimately yielded analogous descriptions of shock-wave formation and behaviour. In the mathematical discussion we can see that each characteristic corresponds to trajectory of a specific point on the waveform depicted in either or space. The history of these characteristics tracks how specific portions of the waveform overtake or lag behind the others. In the case of a set of converging characteristics the point of intersection corresponds to a mathematical singularity and the formation of a shockwave. In the case of diverging characteristics we can see that the waveform points begin smearing out in space - this is clearly analogous to the description of rarefaction waves.
Strong and Weak Shocks
[edit | edit source]In the context of the method of characteristics a shock-wave is any discontinuity produced by the convergence of characteristic lines. A distinction is made between two types of shock solutions depending on how they affect the locus of thermodynamic states. A weak shock is define as the case when the change between final and reference states is nearly identical to that of the equivalent simple, characteristically convergent wave. In this case the process by which the change in states is effected is isentropic and the path through which the material is loaded from the reference state to the final state is described by the isentrope.
Conversely a strong shock is the discontinuous solution for which the locus of all possible states does not coincide with the isentrope but rather a different loading path.
This discussion of state loci will become more clear with the introduction of the Hugoniot.
References
[edit | edit source]- Introduction to Wave Propagation in Nonlinear Fluids and Solids; D.S. Drumheller; 1998
- Explosives Engineering; Paul W. Cooper; 1996
- Shock Waves and Explosions; P.L. Sachdev; 2004



















![{\displaystyle d\zeta ={\frac {\partial \zeta }{\partial x}}[dx-(\nu -C\epsilon )dt]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b79c5700b4e823e95741b53f0eb93da9a44733a)
![{\displaystyle d\xi ={\frac {\partial \xi }{\partial x}}[dx-(\nu +C\epsilon )dt]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3be449f364cb95f24970e911eb02959060a3056b)






















![{\displaystyle \ \nu -\nu ^{0}={\frac {1}{2}}J_{+}\left[t-{\frac {x}{\nu +c}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/177fd3b17dbcd6b0a6e371711a819fb9f4f3d6e7)
![{\displaystyle \ \int _{1}^{\epsilon }{C(\epsilon )\,d\epsilon }=-{\frac {1}{2}}J_{+}\left[t-{\frac {x}{\nu +c}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1aad614ac7768a3f76134ef4bf47e3b9db62d121)


![{\displaystyle \ \nu =m[(\nu +c)t-x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f4804fb204c5c06128bea30f30a51b9b0f7c213)






