Engineering Acoustics/Analogies in aeroacoustics
Acoustic Analogies
[edit | edit source]
A direct way to predict Aerodynamic noise would be to solve the Navier-Stokes Equations in a general three-dimensional unsteady compressible numerical simulations. Unfortunately, it is hardly achievable except for very simple academic configurations within a delimited region. The idea of an acoustic analogy is to restate the full equations of gas dynamics providing an equivalent wave equation in homogeneous medium in uniform motion from the point of view of a distant observer. This condition leads to simplifications of usual linear acoustics problems[1]. The most systematically used formalisms are Lighthill's analogy and the extensions made by Curle and Ffowcs Williams & Hawkings, because they offer of wide range of applicability.
It must be started clearly that the aim of an analogy is not essentially to deduce exacts results or numerical coefficients, but to infer general laws from the standard procedures associated with the classical wave equation. A preliminary knowledge of the main flow features coming from either experiments, CFD or analytical methods is needed to apply these analogies. Moreover, the degree of accuracy in the flow variables to extract acoustic results is crucial to ensure the relevance of the prediction method.
Governing gas dynamics equations to Lighthill's equation
[edit | edit source]References [2] [3], development below originates from Aeroacoustics wikipage.
- ..........................conservation of mass equation (E1)
where and represent the density and velocity of the fluid, which depend on space and time, and is the substantial derivative.
Next is the conservation of momentum equation, which is given by
- ..........................conservation of momentum equation (E2)
where is the thermodynamic pressure, and is the viscous (or traceless) part of the Cauchy stress tensor from the Navier–Stokes equations.
Step 1: Multiplying (E1) by and adding it to (E2) yields
Step 2: Differentiating (E1) with respect to time, taking the divergence of (E2) and subtracting the latter from the former, we get
Step 3: Subtracting , where is the speed of sound in the medium in its equilibrium (or quiescent) state, from both sides of the last equation and rearranging it results in:
which is equivalent to
where is the identity tensor, and denotes the (double) tensor contraction operator.
Using Einstein notation, Lighthill’s equation can be written as
where is the so-called Lighthill's stress tensor , further details are provided in the next section. with: is the inertial[check spelling] stress tensor of Reynolds is the viscous stress tensor of Reynolds represents all effects due to entropy non-homogeneities (important for hot jets with high temperature gradients)
Lighthill's Acoustic Analogy
[edit | edit source]Aeroacoustic engineers need to predict noise arising with turboengines id est localized unsteady flow in a propagating medium, at a first step of approximation. The basic idea of Lighthill (1952) is to reformulate the general equations of gas dynamics, in order to derive a wave equation. The featured variable is the density fluctuation, naturally preferred because acoustic waves in a gas are due to compressibility. No special assumption is made nor linearisation introduced.
- ...............................Lighthill's equation
with : called Lighthill's tensor
This equation remains true if the same quantity is added on both sides. Add the : with being the characteristic speed of sound of the undisturbed gas (precisely the speed of sound in the medium surrounding the flow region, in the applications; this is different from the local speed of sound in the flow). Then, forming a wave operator on the left-hand side and removing all other terms on the right-hand side leads to:
This result is the well-known Lighthill's equation. When applied to a true problem of acoustics, it reduces to the homogeneous wave equation at large distances from the flow, since all terms in the right-hand side can be considered negligible (according to the reasonable assumptions related to the propagation of acoustic waves, as a small-amplitude, isentropic motion[4]). An alternative form of Lighthill's equation can be written with the pressure instead of the density, as follows:
- .....................LightHill equation on the fluctuating pressure
Maybe this one is less common because density fluctuations are directly related to compressible effects, whereas pressure fluctuations can exist to compensate inertial accelerations in the fluid. When temperature non-homogeneities are involved, however, the fluctuating pressure is well suited.
Explanation of each term of Lighthill's tensor:
Aeoracoustic sources can be separate in three distinct categories,

- Monopole sources: Spherical sources or discrete source delivering flow rate fluctuating over the time. Can appear only if solid surfaces are encountered.

- Dipole sources: Similar to two monopoles placed side by side with opposition phase and . Dipoles are associated to the force according to the axe created by our joined monopoles. Like Monopoles they only appear when solid surfaces are involved in the domain.

- Quadrupole sources: Constituted of two dipoles side by side in phase opposition, these sources cames from turbulent vortices and are usually neglected at low velocity flow. They originate from shear-terms in Navier-Stokes equations.
As a consequence of the general equations of gas dynamics, Lighthill's equation is exact. All aeroacoustic processes, including generation of sound by the flow non-homogeneities, sound propagation through the flow and sound dissipation by viscosity or heat conduction, are accounted for. Hence, this equation is not tractable as a pure wave equation using linear acoustics since the right-hand side contains the acoustic field to be determined and cannot be considered as a true source term. Thus we need to approximate this term independently of the acoustic variables which corresponds to neglect some of the mechanisms. To remove this fundamental difficulty, Lighthill proposed some simplifications motivated by the thinking that sound generation by the mixing of fluid is the dominant mechanism , especially at the high Reynolds numbers of interest in aeronautics. This is equivalent to privilege the mechanical effects related to fluid inertia and discard thermodynamic effects as secondary ones.
Lighthill's Approximation
[edit | edit source]Lighthill's equation is well posed because it assumes that sources are contained within the flow and not outside of it. I reduces to the homogeneous wave equation in the propagation region. But in order to solve near the sources approximations using comparison between phenomena has to be done.
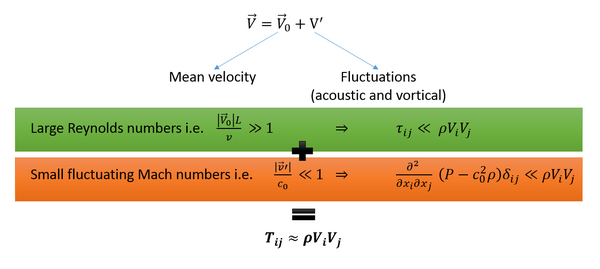
Lighthill's analogy is often use to calculate jet noise, is this type of application we have specific conditions leading to simplifications [5]:
Practical approximation used in industrial context:
The approximation makes the equation explicit in the sense of the wave equation in linear acoustics, to be solved formally by the Green's function technique. When numerical means are used to described the flow, some assumptions can be removed for a more accurate evaluation and the equation used to post-process the flow data.

If entropic non-homogeneities dominate in a disturbed flow, sources appears as equivalent monopoles:
Using Ribner's splitting and uncompressible fluid laws:
Leading to the final approximate Lighthill equation:
.....................approximate Lighthill equation
Ffowcs Williams & Hawkings formulation
[edit | edit source]History
[edit | edit source]In 1969, Ffowcs Williams & Hawkings, are the first scientists to express a fundamental equation to predict noise generate by blades in a flow [6].
Ffowcs Williams & Hawkings general equation
[edit | edit source](They are several formulations of FWH analogy, here is one adapted to blade noise description phenomena)
Deriving from Lighthill's equation, it reveal that fluctuating pressure generating acoustic sources in a rotor is solution of a specific inhomogeneous wave equation:
where, the vector coordinates from a source point and the time in sources domain.
The source term can be written as the following sum:
- First term represents thickness noise generated by volume displacement of fluid. A fan blade has its thickness and volume. As the rotor rotates, the volume of each blade displaces fluid volume, then they consequently fluctuate pressure of near field, and noise is generated. This noise is tonal at the running frequency and generally very weak for cooling fans, because their RPM is relatively low. Therefore, thickness of fan blades hardly affects to electronic cooling fan noise. (This kind of noise can become severe for high speed turbomachines like helicopter rotors.)
- Second term is called loading noise, comes from fluctuation of the force-field on moving surfaces. In a rotor, It originates from nonstationary aerodynamic forces between the fluid and the blades. In computational models, this term is represented by surface-distributed dipoles. (Dominant for fans)
- Final term is shear noise, which is composed of quadrupoles on the surface of the blades [7].
The Ffowcs Williams & Hawkings theory allows to solve this equation knowing the source terms in Green's functions.
Ffowcs Williams & Hawkings extended analogy using permeable control surface
[edit | edit source]In all applications where the quadrupole term is significant and must be calculated, which preferentially occurs at high speeds, the computations can be made cumbersome because the sources are distributed inside a volume, the boundaries of which are not precisely defined. In contrast, the surface source terms are much simpler to compute and clearly delimited. If CFD must be used in a limited domain surrounding the surfaces, and if the computations are able to reproduce the acoustic near-field, a more convenient way of solving the acoustic problem can be proposed by taking the information not on the physical surfaces but on a delocalised control surface that can be user-defined [8]. Double layer potential description can be apply, to solve the Helmotz equation using Bessel functions assumption. This generalised form of Ffowcs Williams & Hawkings’ analogy is widely used in recent Computational Aero-Acoustics (CAA).

N.B: The CFD Domain inside the control surface must be implemented until turbulence systems generated are fully developed (using for example k-criterion).
The formal advantage of an analogy is to state a problem of aeroacoustics as a usual problem of linear acoustics, by defining equivalent sources that would produce in a uniform medium the same sound as what is heard at observer’s location from the flow-and-surface configuration. The difficulty of the initial gas-dynamics equations is transposed to the description of the source terms. The formal solution is derived using the theoretical background of linear acoustics but it may be useless if the equivalent source terms are not determined elsewhere. Using Lighthill and FWH analogies allow engineers to calculate aircraft engines noise for example at a lower time-calculation cost.
Intensive research at NASA and CERFACS facilities try to develop more efficient calculation schemes to provide improved design tools to motorists engineer to gain confidence in noise prediction and develop aero-mechanical-acoustic design for future generation products.
Making approximations means discarding phenomena that are expected negligible and retaining the dominant features. This is just proposing an interpretation.
References
[edit | edit source][1]Goldstein, M. E. (1976). Aeroacoustics. New York, McGraw-Hill International Book Co., 1976. 305 p., 1.
[2]Tam, C. K. (1995). Computational aeroacoustics-Issues and methods. AIAA journal, 33(10), 1788-1796.
[3]Wang, M., Freund, J. B., & Lele, S. K. (2006). Computational prediction of flow-generated sound. Annu. Rev. Fluid Mech., 38, 483-512.
[4]Colonius, T., Lele, S. K., & Moin, P. (1993). Boundary conditions for direct computation of aerodynamic sound generation. AIAA journal, 31(9), 1574-1582.
[5] Williams, J. F. (1969). Hydrodynamic noise. Annual Review of Fluid Mechanics, 1(1), 197-222.
[6] Williams, J. F., & Hawkings, D. L. (1969). Sound generation by turbulence and surfaces in arbitrary motion. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 264(1151), 321-342.
[7] Ianniello, S. (1999). Quadrupole noise predictions through the Ffowcs Williams-Hawkings equation. AIAA journal, 37(9), 1048-1054.
[8]Di Francescantonio, P. (1997). A new boundary integral formulation for the prediction of sound radiation. Journal of Sound and Vibration, 202(4), 491-509.











![{\displaystyle {\frac {\partial ^{2}\rho }{\partial t^{2}}}-c_{0}^{2}\nabla ^{2}\rho =\nabla \cdot \left[\nabla \cdot (\rho \mathbf {v} \otimes \mathbf {v} )-\nabla \cdot \sigma +\nabla p-c_{0}^{2}\nabla \rho \right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/471371077cd60e5c6ef74c2df8a482bfb7f3f688)
![{\displaystyle {\frac {\partial ^{2}\rho }{\partial t^{2}}}-c_{0}^{2}\nabla ^{2}\rho =(\nabla \otimes \nabla ):\left[\rho \mathbf {v} \otimes \mathbf {v} -\sigma +(p-c_{0}^{2}\rho )\mathbb {I} \right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/612e7b49b9ae21a4ad4361a54229226eaeeb7fdc)













![{\displaystyle \ {\frac {\partial ^{2}\rho }{\partial t^{2}}}-c_{0}^{2}{\frac {\partial ^{2}\rho }{\partial x_{j}^{2}}}={\frac {\partial ^{2}}{\partial x_{i}\partial x_{j}}}[\rho V_{i}V_{j}+(P-c_{0}^{2}\rho )\delta _{ij}-\tau _{ij}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2ddb38c9610afcf63ea4e164ed29cc87681cb3b)