Electronics Handbook/Circuits/Current Divider
Jump to navigation
Jump to search
Current Divider
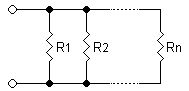
[edit | edit source]If two elements are in parallel, the voltage across them must be the same, but the current divides according to the resistances. A simple circuit with two (or more) resistors in parallel with a source is called a current divider.
Figure B: Parallel Resistors.
Mathmatic Formula
[edit | edit source]If a voltage V appears across the resistors in Figure B with only and for the moment then the current flowing in the circuit, before the division, i is according to Ohms Law.
Using the equivalent resistance for a parallel combination of resistors is
- (1)
The current through according to Ohms Law is
- (2)
Dividing equation (2) by (1)
Similarly
In general with n Resistors the current is
Or possibly more simply
Where