
Consider n inductors in series, as above. The voltage across the whole arrangement (i.e. across the two terminals) must be equal to the sum of the voltages across the individual inductors:

from our definition of inductance, where the voltage is the inductance multiplied by the rate of change of current, we get

where i1 is the current in element 1, and so on. Since the current in every element the series must always be the same (by Kirchhoff's Current Law), we can see that

where i is the current in the network. Factorising, we get:
 .
.
If we now call all the element in the series a single, equivalent inductance, Leq, we see that

Thus,

This means that when in series, the total inductance is just the sum of all the constituent inductances.
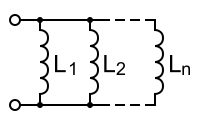
When inductors are in parallel, then each inductor has the same voltage across it, that is, the voltage present at the terminals of the network. This can just be called v. Now, our equation describing the equivalent inductance, Leq, is:

where ieq is the current through the network.
By Kirchhoff's Current Law, we have

Differentiating with respect to time gives

Now by rearranging the general equation describing inductance in the i'th element, we can obtain, for each term in the above,

Substituting into the equation before, we get

Factorising,

Rearranging, we get


So, therefore:


This is identical to the rule for combining resistors.

















