Electronics/Analog multipliers
Analog multipliers
[edit | edit source]An analog multiplier is a circuit with an output that is proportional to the product of two inputs:
where K is a constant value whose dimension is the inverse of a voltage. In general we might expect that the two inputs can be both positive or negative, and so can be the output. Anyway, most of the implementations work only if both inputs are strictly positive: this is not such a limit because we can shift the input and the output in order to have a core working only with positive signals but external interfaces working with any polarity (within certain limits according to the particular configuration).
Two possible implementations will be shown. Both will be using operational amplifiers, but the first one will use diodes to get the needed relationships, the second one MOSFET transistors.
Diode Implementations
[edit | edit source]As known, using operational amplifiers and diodes it's quite easy to obtain the logarithm and the exponential of a certain input. Remembering the property of logarithms:
we can multiply two signals first calculating their logarithm, then summing them and finally calculating the exponential of such a sum. From the point of view of mathematics, such an approach works as long as the two inputs are positive, because the logarithm of a negative number does not exist (in the real domain). We'll see that this limit is valid for the actual circuit as well, even if the reason will be more "physical". The block diagram of this implementation is the following:

If we simply append the circuits for logarithm, sum and exponential we get the following configuration:
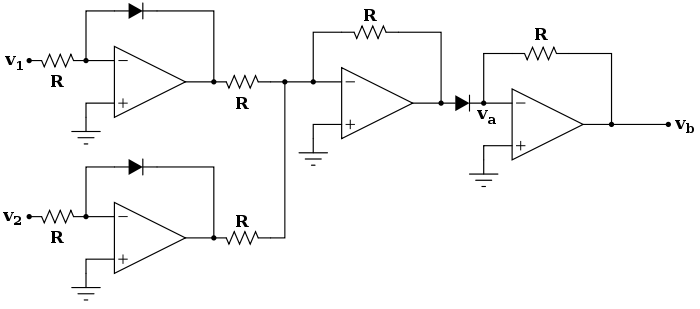
for a quick overview on the behavior of the circuit, we'll assume that all the resistors R have the same value. It is obviously possible to use different values to get different results, but we will not consider it here. Let us use the following notation for the relationship between current and voltage on a diode:
where is the thermal voltage (25..30mV at common operating temperatures) and Is is the current flowing through the diode if it's inverse-polarized. If we analyze the circuit without introducing any approximation we get:
so the final output is:
as it is clear, in the output there is the multiplication we were looking for, but there is another term we don't want. It can't be simply considered an error because it might be as great as the multiplication element, so it has to be removed. Anyway this is an easy task, since it is necessary only to add another stage to sum exactly , so we will have no error. The complete multiplier circuit is the following:

where the output voltage is given by:
that's exactly what we wanted. The circuit works as long as the following relationship is verified:
so the inputs can be zero or sightly negative but, since will be a small voltage, we are allowed to rewrite the relation simply as . From the mathematical point of view this is due to the fact that we can't calculate the logarithm of a negative number, from a physical point of view the limit is due to the fact that we can obtain only very small currents (almost zero) inverse-polarizing the diodes.
In practical applications, the diodes are replaced with BJTs connected so to work like a diode.
MOS implementation
[edit | edit source]
Since it is possible to use a MOSFET transistor as a voltage controlled resistor, it is possible to use this feature to create an analog multiplier. Referring to the picture on the right -- the letters indicate the different pins: Drain, Source and Gate. MOS devices are symmetrical, so the drain and source can be exchanged without affecting the behavior of the device. Use source as the lowest voltage terminal and drain as the higher voltage terminal. When the voltage between gate and drain exceeds the threshold voltage, i.e. , the relationship between current and voltage is the following:
assuming we can always use this relationship, the analog multiplier configuration is the following:

where source and drain of both devices are pointed out. If and are positive, then the sources will be at virtual ground by the operational amplifier. The current flowing through is clear: one side of the resistor has the voltage , the other one is at (virtual) ground. That same current will flow through the MOS , thus defining the voltage . The current is given by:
but and . replacing and calculating we get:
considering the other MOS we have:
where and . Replacing we get:
from which the output voltage is:
which is what is wanted. The difference between the previous configurations are:
- the MOS implementation is simpler and requires fewer devices
- in the calculations for the diode configuration we did not introduce any approximation, while the MOS configuration we did.
In other words, the diode implementation is more complicated but it works fine for a wider range on inputs.




![{\displaystyle v_{a}=-\left[-V_{T}\ln \left({\frac {v_{1}}{RI_{s}}}+1\right)-V_{T}\ln \left({\frac {v_{2}}{RI_{s}}}+1\right)\right]=V_{T}\ln \left[\left({\frac {v_{1}}{RI_{s}}}+1\right)\left({\frac {v_{2}}{RI_{s}}}+1\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/464f91d3f22059653d47a2310afc969fcc613e24)







![{\displaystyle I_{DS}=K[2(V_{GS}-V_{T})V_{DS}-V_{DS}^{2}]\simeq 2K(V_{GS}-V_{T})V_{DS};\qquad V_{GD}>>V_{TH}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/407d308ec81d66e579669b27fbb5593b23627c43)















