Electricity and magnetism/Light
The wave equation
[edit | edit source]In the absence of charges and currents, Maxwell's equations are
We can deduce :
Or ( the proof of this equality, from the definitions of , , and is given at the end of this chapter)
and
so
where
is the wave equation. Its solutions are waves that propagate at the speed of light, or superpositions of such waves.
Plane waves
[edit | edit source]A wave that propagates throughout space is a function of 4 variables, x, y, z and t, 3 space coordinates and one time coordinate. is the field at the point
To understand a plane wave, we can think of a mille-feuille whose leaves can slide over each other. A wave can then propagate in the direction perpendicular to the leaves. If a moving leaf carries its two neighbors and is carried by them, a movement on one side of the mille-feuille can propagate to the other side. This propagation movement is a plane wave.
If the direction of propagation is the x axis, the leaves are vertical planes and the movement of a point does not depend on its position on the leaf, it only depends on its x abscissa. A plane wave can therefore be represented by a function which depends only on a spatial coordinate x and time t. It is a one-dimensional wave, because it depends only on one spatial coordinate.
If, moreover, the leaves always move in the same vertical direction, their movement can be measured by a single number, their movement in the vertical direction. The plane wave can then be represented by a function whose value is a single real number. If the motion were more complicated, would be a vector.
Let be a real function of a single real variable. is a real number that depends only on the real number .
can represent any curved line in a plane that never goes back, extending infinitely from left to right. This way, for each , there is a unique point on the line whose coordinate is . The distance from this point to the horizontal axis is .
Let be the real function of two real variables, defined by
represents a plane wave which propagates without distortion at speed . The sign of determines the direction of propagation. The mille-feuille is deformed by the propagation of the wave, but the shape of this deformation does not change. It remains the same throughout its journey. Such a wave can therefore transmit a message from one point to another, as far away as we want. is the signal propagation speed.
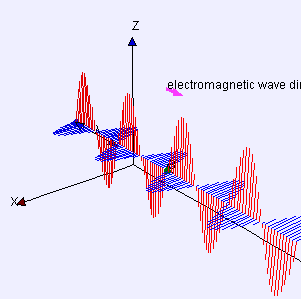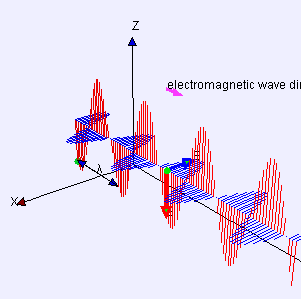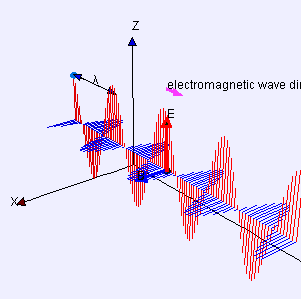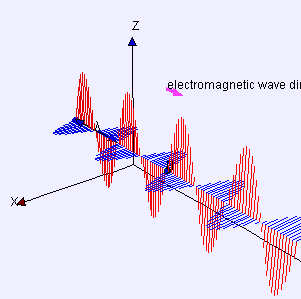
An electromagnetic wave is a wave of an electric force and magnetic force which propagates at the speed of the light :
The wave is a solution of the wave equation
Proof :
As does not depend on y or z,
so
Now
We can show in the same way that
So for all x and all t.
Are electromagnetic waves mechanical?
[edit | edit source]A mechanical wave is a wave that propagates by setting masses in motion:
Maxwell believed that electromagnetic waves were similar to mechanical waves that propagate in a material medium, which he called the ether, and which was supposed to fill the entire Universe, since light propagates everywhere, and because mechanical waves like sound do not propagate in a vacuum.
When a wave is mechanical, its material support does not propagate. The moving masses oscillate around an equilibrium position. In a homogeneous and isotropic medium, the speed of wave propagation is the same in all directions. It is the speed of the wave relative to its material support, which we measure when we are at rest in relation to this support. If we are moving relative to the material support, the speed of the waves is not the same in all directions.
If light propagated in the ether, we would have to observe this dependence of its speed on its direction, because we cannot always be at rest with respect to the ether. We tried to observe it, but we never succeeded.
The theory of relativity posits that the speed of light is always the same for all observers, regardless of their motion. This is absurd from a classical point of view because the speeds measured by observers in relative motion are always different. Einstein showed that there is however no contradiction, provided that we admit that the simultaneity of events depends on the movement of the person observing them. According to Einstein, time is not absolute, because the simultaneity of events is not absolute, but relative to the observer.
If light propagated in the ether, the measurement of its speed would depend on the movement of the observer relative to the ether. So the theory of relativity dictates that the ether does not exist. Light is a wave without material support.
Electromagnetic waves are waves of electric and magnetic force that propagate in a vacuum. They are not mechanical waves because they can propagate without putting masses in motion.
Monochromatic waves
[edit | edit source]A wave is monochromatic with frequency if and only if for all and all ,
is the angular frequency, or the pulsation..
A monochromatic sound wave is pure sound. The higher its frequency, the more high-pitched it is.
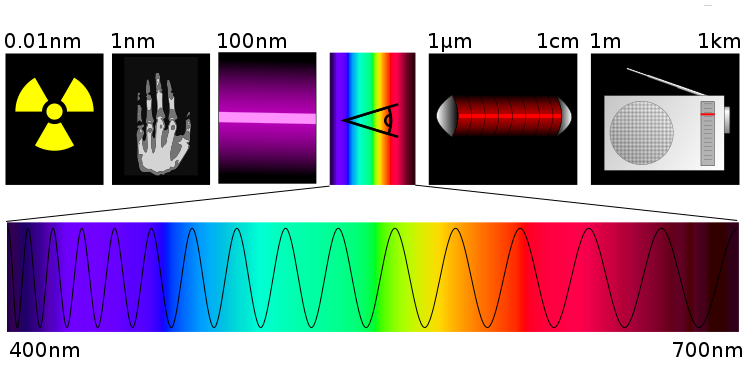
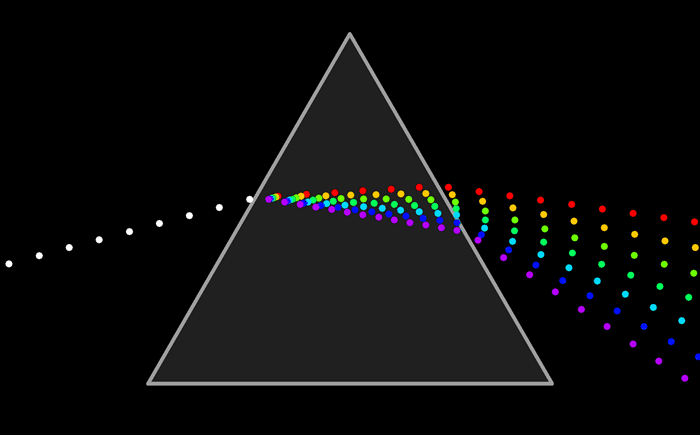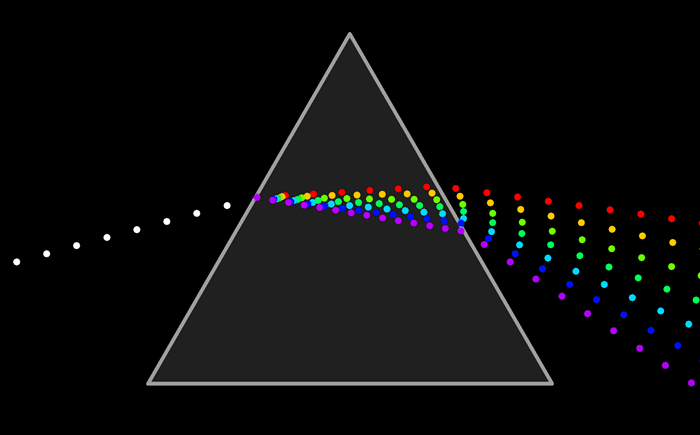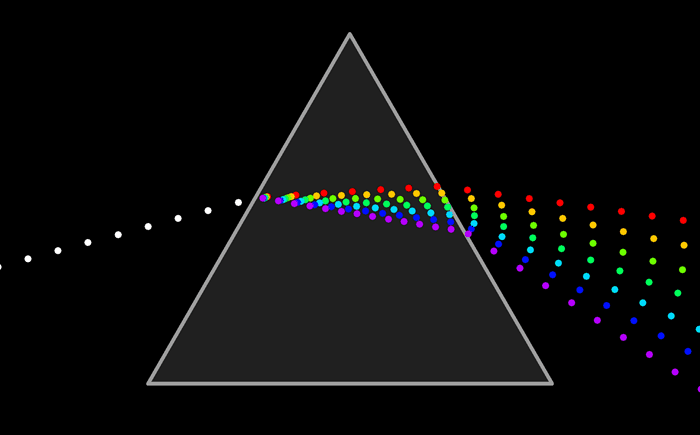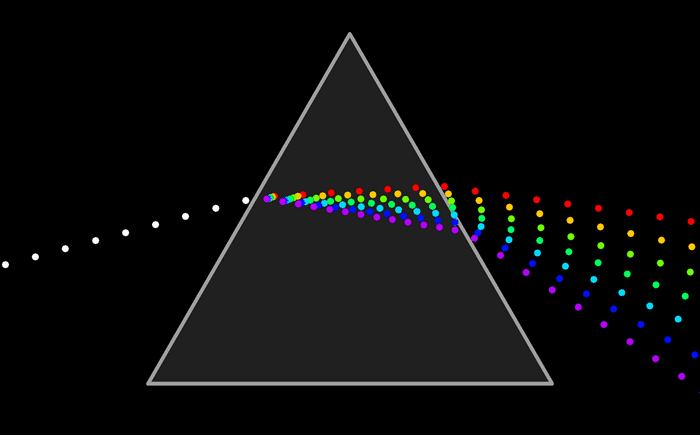
A monochromatic light wave is a pure color, one of the colors of the rainbow, but extremely bright, as if we could see the rainbow in front of the night sky. Low frequency light is red. If we increase the frequency, we reach violet, the highest frequency, passing through orange, yellow, green and blue, in that order. Beyond violet, we find ultraviolet, X-rays and rays. Below red, we find infrared, microwaves and radio waves, the frequency of which can be as low as we want.
White light is a superposition of monochromatic lights. A rainbow and a prism sparate the components of white light and thus reveal its spectrum, that is to say its composition in monochromatic lights:
A monochromatic plane wave of pulsation which propagates at speed is represented by a function such that
where is a constant, , is the wavelength.
The definitions of , , , and lead to
The superposition of waves
[edit | edit source]If and are two wave solutions of the wave equation , then is also a wave solution of the wave equation.
Proof: the derivative of a sum is the sum of the derivatives, so and .
Photons are particles of light. Electromagnetic waves represent their movements. Photons do not collide. An illuminated object can emit light without being hindered by the light illuminating it, because light going in one direction is not hindered by light going in the other direction. Photons can pass through each other without knowing each other, as if each could pass through the other. The superposition of waves explains this mutual indifference of photons. Two waves propagating in opposite directions are superposed at the point where they meet, and this superposition does not affect their propagation.
The superposition of waves is a very general principle with which most phenomena are explained, in particular the decomposition of white light, because it is a superposition of monochromatic waves.
Standing waves
[edit | edit source]A wave is stationary if and only if for all and all ,
Such a wave does not propagate. The shape defined by vibrates in place but does not move.
The vibrations of a string stretched at its ends and the surface of a drum are standing sound waves. The vibrations of air enclosed in a cavity, such as inside a guitar, are also standing sound waves.
Let and be two identical monochromatic plane waves, except that they propagate in opposite directions.
is a standing wave.
Proof: . So
If light is trapped between two parallel mirrors, both perpendicular to its direction of propagation, it is reflected on the two mirrors and therefore propagates at the same time in two opposite directions. It thus produces a standing wave. Light trapped between two mirrors inside a laser is a standing wave.
The reflection of light
[edit | edit source]Sound waves are pressure waves. All bodies, solid, liquid or gaseous, can vibrate. When they vibrate, they cause neighboring bodies to vibrate. This vibration is sound. When it is transmitted through the air to an ear, it vibrates its eardrum, which is like the surface of a very small drum. This vibration is transformed by neurons into electrical signals which propagate to the brain.
Sound is also a density wave, because the pressure of bodies depends on their density.
Sound is also a wave of velocity, because in the absence of movement, the density of bodies is constant.
Echo is the reflection of sound off a cliff or wall, in the same way that light is reflected by a mirror.
A soft wall does not reflect sound. The harder the wall, the better it reverberates sound. The reverberation of sound is its reflection, its bouncing off the hard walls.
A very hard wall does not vibrate, or almost not. Its velocity field is zero. The same goes for the air in contact with it.
A wave on the surface of the water is reflected because it must remain horizontal, perpendicular to the wall which reflects it. So its slope is equal to zero.
If a mirror is metallic, the electric field parallel to its surface is zero, or almost zero, because the electric charges are mobile, they are constantly moving so as to cancel the electric forces that move them. A metal mirror behaves towards light like a hard wall towards sound waves, because it cancels the electric field parallel to its surface.
Consider a plane wave which propagates without deformation towards the right (increasing x) emitted at a point located at in the direction of a reflecting wall located at . is determined by its movement at , which can be the emitting source of the wave.
because
We seek a solution of the wave equation such that for all t, since the field must cancel on the reflective wall.
By definition of , for all .
is the superposition of two waves that are symmetrical to each other. One is the reflection of the opposite of the other relative to the reflecting wall. The two waves and propagate in opposite directions. The wave could be emitted by a point at which has a movement opposite to that of the initial emitter:
Everything happens as if the reflecting wall produced a wave emitted by a body exactly symmetrical to the body emitting the initial wave. It's the mirror effect. We see in a mirror as if the bodies in front of it were present behind it.
Electromagnetism therefore explains why metal surfaces are always shiny and reflective.
Rough surfaces also reflect light, unless they are black and perfectly absorbent. But they do not have the effect of a mirror:
The eye and the formation of images
[edit | edit source]For an image to form, it is enough for each point on the image plane to receive the light emitted by a single point on the object. The wider the light source that illuminates a point in the image, the blurrier the image.
We can see an image on a white wall in a dark room if we let the light pass through a small hole made through the shutters. We can thus see the sunny opposite facade projected upside down on a wall or on a white sheet. Each point on the wall receives light from a single point on the facade if the hole is very small. If the hole is large the image is blurry.
A curved interface between two transparent materials has the property of making the light passing through it converge, or diverge.
Images form at the back of the eye, upside down, because light from one point on an object converges on a single point at the back of the eye.
We explain the propagation of light in transparent materials with Maxwell's equations. The formation of images is therefore also a consequence of Maxwell's equations.
The refraction of light
[edit | edit source]Refraction of light explains why a stick appears broken by the surface of water and why lenses can cause light waves to converge or diverge.
Refraction is explained by the difference in the speed of propagation of light between two transparent materials. Light is always slower in transparent materials than in a vacuum, 300,000 km/s. In the air this slowdown is very slight, but in water its speed is almost 215,000 km/s, and in a diamond it goes down to 125,000 km/s.
When the direction of propagation of light is perpendicular to the surface between the two materials it passes through, it is not modified:
But the light is all the more deviated as its initial direction of propagation deviates from the perpendicular to the surface:
If we have our heads underwater and look at the edge of the pool, beings seem to be further away than they really are:
Conversely, if we are in the air, and if we look at beings underwater, they appear to be closer than they actually are. This is why the sticks appear to be broken by the water surface:
We see in this photograph that the brush is broken by the surface of the water and that it is enlarged by the curved surface of the glass, as if this surface was were a magnifying glass.
Light always obeys Fermat's principle: the path followed by light is always the shortest among all possible paths.
A lifeguard is on a beach. If the person she has to save from drowning is in front of her, she chooses the shortest path, which is in a straight line, perpendicular to the line of the beach. If the future rescued person is not in front of her, she must not go in a straight line, because she runs faster on the beach than she swims in the water. She must therefore choose a broken line as her trajectory, first running on the beach to be almost in front of the future rescued person, then swimming. Light does the same when it passes from air into water.
Intelligence is to choose the best among the possibilities, or at least a satisfactory one. Light always chooses the shortest path, because there is no time to lose.
The slowing of light in water and other transparent materials is explained with the Maxwell and Lorentz equations. When light passes through a material, its charges begin to move and themselves become light-emitting sources. The superposition of the incident wave and the induced waves is the cause of the reduction in the speed of the resulting wave, and therefore of the refraction of light.
Interference
[edit | edit source]One of the most astonishing consequences of the principle of superposition is that light plus light can equal darkness:
The energy of the light we observe is proportional to , the scalar square of the electric field it propagates. If two light sources produce equal and opposite electric fields, their superposition produces a zero field, without energy, therefore an absence of light, darkness.
In Young's slit experiment, two slits allow light to pass through. If we observe the light on a screen which receives it, we see an alternation of dark and bright fringes, but the dark parts are illuminated by the two slits like the bright parts:
Young understood in 1803 that waves in opposite directions cancel each other out while they add up when they have the same direction:
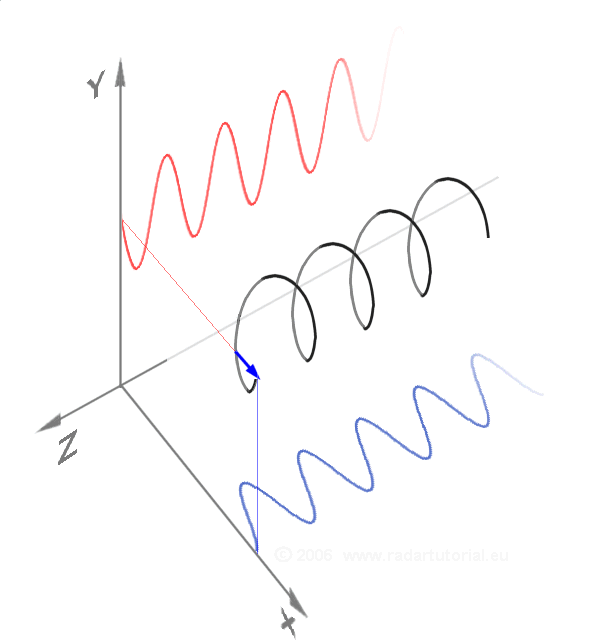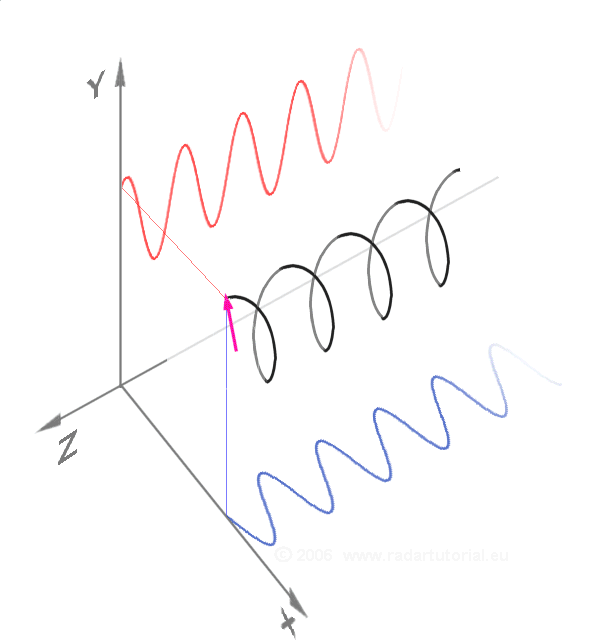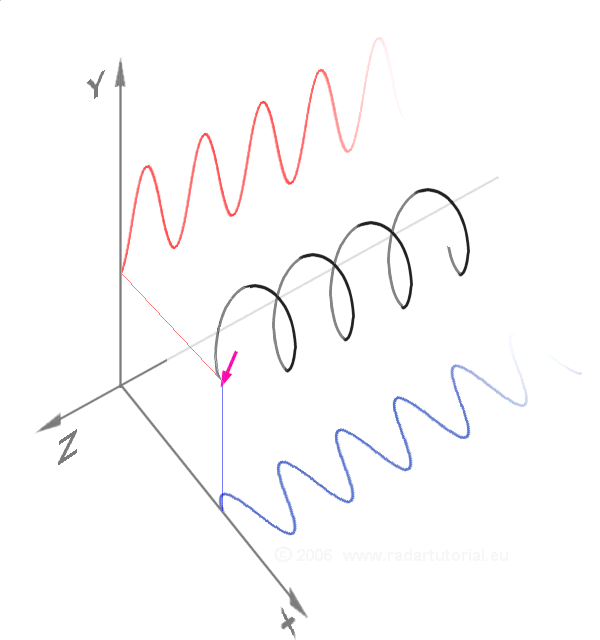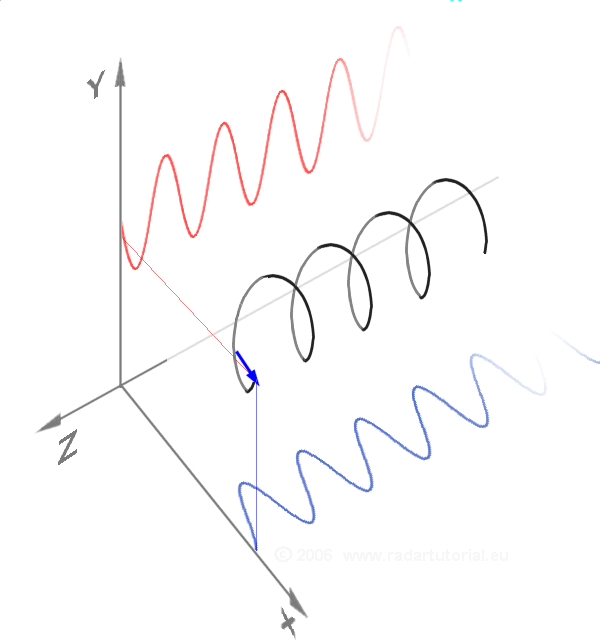
The polarization of light
[edit | edit source]Sunglasses sometimes have polarized lenses:
Light is linearly polarized when it has a direction perpendicular to its direction of propagation. A polarizer is a filter that stops light polarized in one direction and lets it pass if it is polarized in the perpendicular direction.
Circular polarization is a superposition of two linearly polarized waves:
When light is circularly polarized, it has a direction of rotation around its direction of propagation. For quantum physics, the polarization of light is the spin of photons. Photons have spin means that they have rotational inertia, like spinning tops. Rotational inertia is what makes a body maintain the same axis and the same speed of rotation. It is what keeps the moving bicycles in balance. Stationary bicycles do not have this balance, because their wheels do not turn.
Light from the Sun or from incandescent light-emitting materials is not polarized. But the light in the sky is polarized. The light obtained by reflection on a mirror, on water or on a glass can also be polarized.
To see if the light is polarized, simply look at it through a polarizing glass that is rotated around an axis perpendicular to its surface:
These two photographs were taken with a polarizer filter that was rotated 90° between the left and right images.
When we put a material under stress, it generally behaves like a polarizer. This polarization effect reveals the stress:
If we place a crystal between two crossed polarizers that we rotate, we can obtain very beautiful effects, because birefringent crystals behave like polarizers:
Maxwell's equations show that the direction of linearly polarized light is the direction of the electric field .
and are always perpendicular to the direction of propagation of an electromagnetic wave.
Proof for a plane wave: the partial derivatives with respect to y and z are zero, since the field depends neither on y nor on z. According to Maxwell's fourth equation, the component in the direction of propagation of the electric field is such that . Since cannot vary over time, it cannot propagate a wave. It is therefore zero for a propagating wave. The same argument holds for from Maxwell's third equation.
Let there be light
[edit | edit source]The Maxwell and Lorentz equations predict the existence of light and all its properties: its propagation, its colors, its standing waves, its reflection, why it forms images, its refraction, its interference and its polarization. They make it possible to study most of the properties of matter (except its radioactivity, which is of nuclear origin, and its gravity) and its interactions with light.
The electromagnetic field has an autonomous existence. Once accelerated electrical charges produce light, it propagates on its own, and the charges that produced it can no longer stop it.
By giving Maxwell's equations (or Coulomb's law and the relativistic geometry of space-time) God gave the laws which make that light can exist, that we can see it and that we can see the world thanks to it. God said “Let there be light” giving the laws of electromagnetism, the equations of Maxwell and Lorentz.
The nabla operator
[edit | edit source]The gradient of a scalar field, the divergence and the rotational of a vector field are the three fundamental operators with which physicists do most of their calculations, particularly in electrodynamics and fluid dynamics. All three can be written with the nabla operator:
can therefore be written:
Proof of :
The calculation is similar for the other two components.