Econometric Theory/Classical Normal Linear Regression Model (CNLRM)
Econometrics is all about causality. Economics is full of theory of how one thing causes another: increases in prices cause demand to decrease, better education causes people to become richer, etc. So to be able to test this theory, economists find data (such as price and quantity of a good, or notes on a population's education and wealth levels). However, when this data is placed on a plot, it rarely makes neat lines that are presented in introductory economics text books.
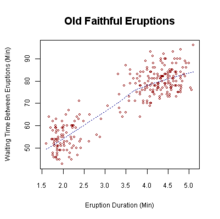
Data always comes out looking like a cloud, and without using proper techniques, it is impossible to determine if this cloud gives any useful information. Econometrics is a tool to establish correlation and hopefully later, causality, using collected data points. We do this by creating an explanatory function from the data. The function is linear model and is estimated by minimizing the squared distance from the data to the line. The distance is considered an error term. This is the process of linear regression.
The Line
[edit | edit source]The point of econometrics is establishing a correlation, and hopefully, causality between two variables. The easiest way to do this is to make a line. The slope of the line will say "if we increase x by so much, then y will increase by this much" and we have an intercept that gives us the value of y when x = 0.
The equation for a line is y = a + b*x (note:a and b take on different written forms, such as alpha and beta, or beta(0) beta(1) but they always mean "intercept" and "slope").
The problem is developing a line that fits our data. Because our data is scattered, and non-linear, it is impossible for this simple line to hit every data point. So we set our line up so that it minimizes the errors (and we need to actually minimize the squared errors). We adjust our first line, or explanatory function to have an error term, so that, given x and the error term, we can correctly come up with the right y.
y = a + b*x + error
Basic Example
[edit | edit source]After blowing our grant money on a vacation, we are pressured by the University to come up with some answers about movements of the sweater industry in Minnesota. We do not have much time, so we only collect data from two different clothing stores in Minnesota on two separate days. Fortunately for us, we get data from one day in the summer and one day in the winter. We ask both stores to tell us how many sweaters they have sold and they tell us the truth. We are looking to see how weather (temperature—independent variable) affects how many sweaters are sold (dependent variable).
We come up with the following scatter plot.
Now we can add a line (a function) to tell us the relationship of these two variables. We will minimize the sum of errors, and see what we get. The distance to the line from the cold side is +15 and the difference from the hot side to the line is -15. When we add them together, we get 15 - 15 = 0. 0 error, our line must be perfect!
Notice that our line fits the data well. The differences between the data and the function are evenly distributed (). So there is a relationship between temperature and sweater sales. "Hot weather increases Sweater Sales" will be the title of our famous paper! But it will be wrong, and we'll probably be fired from our job at the University.
If we had only minimized the absolute distances between the line and the data! Well, here is a plot with an estimated line that does just that. To do this, we minimize the sum of squared errors.
Once we minimize the absolute distances between the line and the data, we have a better fit and we can declare that "cold weather increases Sweater Sales" ()
Basic bivariate model
[edit | edit source]Our basic model is a line that best fits the data.
Where and , α and β are unknown parameters that must be estimated. is the unobserved error term. This term is an iid random variable. regression coefficient.
Notes on Notation:
| Symbol | meaning |
|---|---|
| Y | Dependent Variable |
| X | Independent Variable(s) |
| α,β | Regression Coefficients |
| ε,u | Error or Disturbance term |
| ^ | Hat: Estimated |
Properties of the error term
[edit | edit source]The error term, also known as the disturbance term, is the unobserved random component which explains the difference between and . This term is the combination of four different effects.
1. Omitted Variables: in many cases, it is hard to account for every variability in the system. Cold weather increases sweater sales, but the price of heating oil may also have an effect. This was not accounted in our original model, but may be explained in our error term.
2. Nonlinearities: The actual relationship may not be linear, but all we have is a linear modeling system. At 30 degrees, 10 people buy sweaters. At 20 degrees 40 people buy sweaters. At 10 degrees 80 people buy sweaters. In our model, the error term does not take into account this nonlinearity.
3. Measurement errors: Sometimes data was not collected 100% correctly. The store told us that 10 people bought sweaters that day, but after we talked to them, 4 more people bought sweaters. The relationship still exists, but we have some error collected in the error term.
4. Unpredictable effects: No matter how well the economic model is specified, there will always be some sort of stochasticity that affects it. These effects will be accounted for by the error term.
Looking again at our OLS line in our sweater story, we a can have a look at our error terms. The error, is the distance from our data Y and our estimate Ŷ. We get an equation from this:



![{\displaystyle Y_{i}\in [1,n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d65c458cf137609df69912d78ecb0a9295a131e)
![{\displaystyle X_{i}\in [1,n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3c7780d45e3ff2dda69a53370c54a5d3e6b4fb3)
![{\displaystyle \epsilon _{i}\in [1,n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fdac3b0a1e081c8fa7f5d9ee866a9236adc6a86)


