Digital Circuits/CORDIC

A CORDIC (standing for COordinate Rotation DIgital Computer) is a circuit to compute several common mathematical functions, such as trigonometric, hyperbolic and exponential functions.

Application

A CORDIC uses only adders to compute the result, with the benefit that it can therefore be implemented using relatively basic hardware.

Methods such as power series or table lookups usually need multiplications to be performed. If a hardware multiplier is not available, a CORDIC is generally faster, but if a multiplier can be used, other methods may be faster.

CORDICs can also be implemented in many ways, including a single-stage iterative method, which requires very few gates when compared to multiplier circuits. Also, CORDICs can compute many functions with precisely the same hardware, so they are ideal for applications with an emphasis on reduction of cost (e.g. by reducing gate counts in FPGAs) over speed. An example of this priority is in pocket calculators, where CORDICs are very frequently used.

History

The CORDIC was invented in 1959 by J.E. Volder, in the aeroelectronics departments of Convair, and was designed for the B-58 Hustler bomber's navigational computer to replace an analogue resolver, a device that computed trigonometric functions.

In 1971, J.S. Walther, at Hewlett-Packard, extended the method to calculate hyperbolic and exponential functions, logarithms, multiplications, divisions, and square roots.

General Concept

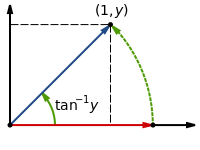
Consider the following rotations of vectors:

Start at (1, 0) Rotate by θ We get (cosθ, sinθ)	Start at (1, y) Rotate until y = 0 The rotation is tan−1y

If we were to have a computationally efficient method of rotating a vector, we can directly evaluate sine, cosine and arctan functions. However, rotation by an arbitrary angle is non-trivial (you have to know the sine and cosines, which is precisely what we don't have). We use two methods to make it easier:

• Instead of performing rotations, we perform "pseudorotations", which are easier to compute.
• Construct the desired angle θ from a sum of special angles, α_i:

$\theta = \alpha_1 + \alpha_2 + \ldots + \alpha_m$

The diagram belows shows a rotation and pseudo-rotation of a vector of length R_i about an angle of a_i about the origin:

A rotation about the origin produces the following co-ordinates:

x_{i + 1} = x_icos α_i − y_isin α_i

y_{i + 1} = y_icos α_i − y_isin α_i

θ_{i + 1} = θ_i − α_i

Recall the identity $\cos \theta \equiv 1 \Big / \sqrt{1+ \tan^2 \theta }$.

$x_{i+1} = \left( x_i - y_i \tan \alpha_i \right) \Big / \sqrt{1+ \tan^2 \alpha_i }$

$y_{i+1} = \left( y_i - x_i \tan \alpha_i \right) \Big / \sqrt{1+ \tan^2 \alpha_i }$

Our strategy will be to eliminate the factor of $1 \Big / \sqrt{1+ \tan^2 \alpha_i}$ and somehow remove the multiplication by tan α_i. A pseudo-rotation produces a vector with the same angle as the rotated vector, but with a different length. In fact, the pseudo-rotation changes the length to:

$R_{i+1} = \frac{R_i}{\cos \alpha_i } = R_i \sqrt{ 1+ \tan^2 \alpha_i }$

Thus we now have these co-ordinates following a pseudo-rotation:

$x^\prime_{i+1} = \left( x_i - y_i \tan \alpha_i \right)$

$y^\prime_{i+1} = \left( y_i - x_i \tan \alpha_i \right)$

θ_{i + 1} = θ_i − α_i

The pseudo-rotation has succeeded in removing our length-factor, which would have required a costly division operation. However, the vector will grow by a factor of K over a sequence of n pseudo-rotations:

$K = \prod_{i=0}^{n-1} \sqrt{ 1+ \tan^2 \alpha_i }$

The co-ordinates following the n pseudo-rotations are then:

$x_{n} = K \left( x_i \cos \sum_{i=0}^{n-1} {\alpha_i} - y_i \sin \sum_{i=0}^{n-1}\alpha_i \right)$

$y_{n} = K \left( y_i \sum_{i=0}^{n-1}\cos \alpha_i - y_i \sin \sum_{i=0}^{n-1}\alpha_i \right)$

$\theta_{n} = \theta_i - \sum_{i=0}^{n-1}{\alpha_i}$

The first three pseudo-rotations. Note how we converge on the correct angle, θ

If the angles are always the same set, then K is fixed, and can be accounted for later. We choose these angle according to two criteria:

• We must also choose the angles so that any angle can be constructed from the sum of all them, with appropriate signs.
• We make all tan α_i a power of 2, so that the multiplication can be performed by a simple logical shift of a binary number.

The tangent function has a monotonically increasing gradient on the interval [0, π/2], so the tangent of a given angle is always less than twice the tangent of half the angle. This means that if we make the angles α_i = tan  ^{− 1}2 ^{− i}, we can satify both criteria. Note that the tangent function is odd, which means that to pseudo-rotate the other way, you just subtract, rather than add, the tangent of the angle.

i	αi = tan−1 (2−i)
	Degrees	Radians
0	45.00	0.7854
1	26.57	0.4636
2	14.04	0.2450
3	7.13	0.1244
4	3.58	0.0624
5	1.79	0.0312
6	0.90	0.0160
7	0.45	0.0080
8	0.22	0.0040
9	0.11	0.0020

In step i of the process, we pseudo-rotate by $d_i 2^{-i}\,$, where $d_i\,$ is the direction (or sign) of the rotation, which will be chosen at each step to force the angle to converge to the desired final rotation. For example, consider an rotation of 28°:

$28 \approx 45.0 - 26.57 + 14.04 - 7.13 + 3.58 - 1.79 +0.90 - 0.45 + 0.22 + 0.11$

$28 \approx 27.91$

Them more steps we take, the better the approximation that we can make by successive rotations. Thus, we have the following iterative co-ordinate calculation:

x_{i + 1} = x_i − d_iy_i2 ^{− i}

x_{i + 1} = y_i + d_ix_i2 ^{− i}

θ_{i + 1} = θ_i − d_iα_i

In order to achieve k bit of precision, k iterations are needed, because $\tan^{-1} 2^{-i} \lessapprox 2^{-i}$, converging as i increases.

Using CORDICs

CORDICs can be used to compute many functions. A CORDIC has three inputs, x₀, y₀, and z₀. Depending on the inputs to the CORDIC, various results can be produced at the outputs x_n, y_n, and z_n.

Using CORDIC in rotation mode

xi + 1 = xi − diyi2 − i yi + 1 = yi + dixi2 − i zi + 1 = zi − diαi

$x_{n} = K \left( x_0 \cos \theta_0 - y_0 \sin \theta_0 \right)$ $y_{n} = K \left( y_0 \cos \theta_0 + x_0 \sin \theta_0 \right)$ zn = 0

For convergence of θ_n to 0, choose d_i = sgn z_i.

If we start with x₀ = 1/K and y₀=0, at the end of the process, we find x_n=cos z₀ and y_n=sin θ₀.

The domain of convergence is $99.7^{\circ} < z_{0} < 99.7^{\circ}$ because 99.7° is the sum of all angles in the list.

Using CORDIC in vectoring mode

xi + 1 = xi − diyi2 − i yi + 1 = yi + dixi2 − i zi + 1 = zi − diαi

$x_{n} = K \sqrt{ x^2 + y^2}$ yn = 0 $z_{n} = z_0 + \tan^{-1} \left( y_0 / x_0 \right)$

For convergence of y_n to 0, choose d_i = − sgn (x_iy_i).

If we start with x₀ = 1 and z₀ = 0, we find z_n=tan⁻¹y₀

Implementations of CORDICs

Bit-parallel, unrolled

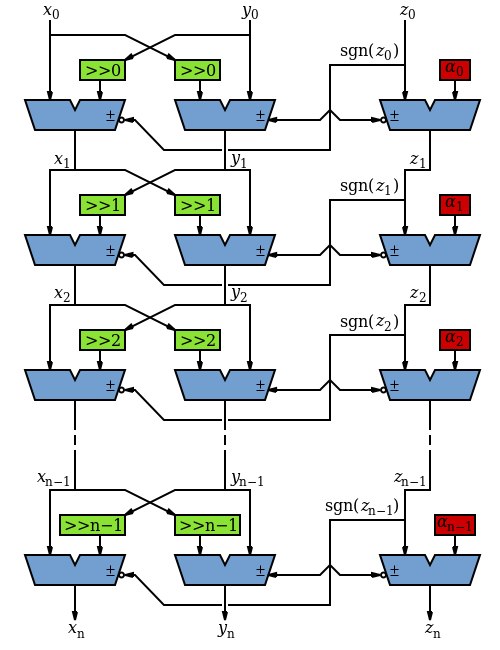
Bit-parallel, iterative

If a high speed is not required, this can be implemented with a single adder and a single shifter.

The Universal CORDIC

By introducing a factor μ, we can also cater for linear and hyperbolic functions:

x_{i + 1} = x_i − μd_iy_i2 ^{− i}

y_{i + 1} = y_i + d_ix_i2 ^{− i}

z_{i + 1} = z_i − d_iα_i

Summary of Universal CORDIC implementations

x_{i + 1} = x_i − μd_iy_i2 ^{− i}

y_{i + 1} = y_i + d_ix_i2 ^{− i}

z_{i + 1} = z_i − d_iα_i

Mode	Rotation	Vectoring
	$d_i = \mbox{sgn } (z_i), \quad z \rightarrow 0$	$d_i = -\mbox{sgn } (x_i y_i), \quad y \rightarrow 0$
Circular μ = 1 αi = tan−12−i
Linear μ = 0 αi = 2−i
Hyperbolic μ = -1 αi = tanh−12−i
In hyperbolic mode, iterations 4, 13, 40, 121, ..., j, 3j+1,... must be repeated. The constant K' given below accounts for this. K = 1.646760258121... 1/K = 0.607252935009... K' = 0.8281593609602... 1/K' = 1.207497067763...

Directly computable functions

$\sin z\,$	$\cos z\,$
$\tan^{-1} z\,$	$\sinh z\,$
$\cosh z\,$	$\tanh^{-1} z\,$
x / y	xz
$\tan^{-1} (y/x)\,$	$\sqrt{ x^2 + y^2 }$
$\sqrt{ x^2 - y^2 }$	ez = sinh z + cosh z

Indirectly computable functions

In addition to the above functions, a number of other functions can be produced by combining the results of previous computations:

$\tan z = \frac{\sin z}{\cos z}\,$	$\cos^{-1} w = \tan^{-1} \frac{\sqrt{1-w^2}}{w}$
$\tanh z = \frac{\sinh z}{\cosh z}$	$\sin^{-1} w = \tan^{-1} \frac{w}{\sqrt{1-w^2}}$
$\ln w = 2 \tanh^{-1} \left| \frac{w-1}{w+1} \right|$	$\log_b w = {\ln w \over \ln b}$
wt = etln w	$\cosh^{-1} = \ln \left( w + \sqrt{1-w^2} \right)$
$\tan^{-1} (y/x)\,$	$\sinh^{-1} = \ln \left( w + \sqrt{1+w^2} \right)$
$\sqrt{ x^2 - y^2 }$	$\sqrt{w} = \sqrt{ (w+1/4)^2 - (w-1/4)^2 }$

Further Reading

• Volder, J.E. (1959), " The CORDIC trigonometric computing technique", IRE Transactions on Electronic Computers 8 (3): 330–334, http://lapwww.epfl.ch/courses/comparith/Papers/3-Volder_CORDIC.pdf, retrieved 2009-06-02 
• Walther, J.S. (1971), "A unified algorithm for elementary functions" (w), Proceedings of the May 18-20, 1971, spring joint computer conference: 379-385, http://portal.acm.org/citation.cfm?id=1478786.1478840, retrieved 2009-06-02 
• Parhami, B. (1999), Computer arithmetic: algorithms and hardware designs