Cyberbotics' Robot Curriculum/Getting started
The first section of this chapter (section Explanations about the Practical Part) explains how to use this document. It presents the formalism of the practical part, i.e., the terminology, the used icons, etc.
The following sections will help you to configure your environment. For profiting as much as possible of this document, you need Webots, an e-puck and a Bluetooth connection between both of them. Nevertheless, if you haven't any e-puck, you can still practice a lot of exercises. Before starting the exercises you need to setup these systems. So please refer to the following sections:
- e-puck page in the User Guide provides many complementary information about the e-puck use in Webots.
- Section Get Webots and install it describes how to install Webots on your computer.
- Section Bluetooth Installation and Configuration describes how to create a Bluetooth connection between your computer and your e-puck.
- Section Open Webots describes how to launch Webots.
- Section E-puck Prerequisites describes how to update your e-puck's firmware.
- Tutorial Chapter in the User Guide describes how to model your own world with Webots.
If you want to go further with Webots you can consider the online user guide User Guide or the Reference Manual.
Explanations about the Practical Part
[edit | edit source]Throughout the practical part, you will find different symbols. They have the following meaning:
![]() : When this symbol occurs, you are invited to answer a question. The questions are related either to the current exercise or to a more general topic. They are referenced by a number which has the following form: "[Q."+question number+"]". For example, the third question of the exercise will have the [Q.3] number.
: When this symbol occurs, you are invited to answer a question. The questions are related either to the current exercise or to a more general topic. They are referenced by a number which has the following form: "[Q."+question number+"]". For example, the third question of the exercise will have the [Q.3] number.
![]() : When this symbol occurs, you will be invited to practice. For example you will have to program your robot to obtain a specific behavior. They are referenced by a number which has the following form: "[P."+question number+"]".
: When this symbol occurs, you will be invited to practice. For example you will have to program your robot to obtain a specific behavior. They are referenced by a number which has the following form: "[P."+question number+"]".
![]() : When this symbol occurs, only the users who work with a Linux operating system are invited to read what follows. Note that this curriculum was written using Ubuntu Linux.
: When this symbol occurs, only the users who work with a Linux operating system are invited to read what follows. Note that this curriculum was written using Ubuntu Linux.
![]() : Ibid for the Windows operating system. Note that this curriculum was also written using Windows XP.
: Ibid for the Windows operating system. Note that this curriculum was also written using Windows XP.
![]() : Ibid for Mac OS X operating system.
: Ibid for Mac OS X operating system.
Each section of this document corresponds to an exercise. Each exercise title finishes with its level between square brackets (for example : [Novice]). When an exercise title, a question number or a practical part number is bounded by the star character (for example: *[Q.5]*), it means that this part is optional, i.e., this part is not essential for the global understanding of the problem but is recommended for accruing your knowledge. They can also be followed by the [Challenge] tag. This tag means that this part is more difficult than the others, and that it is optional.
Get Webots and install it
[edit | edit source]The easiest way to obtain Webots is to visit the following website:
https://www.cyberbotics.com/doc/guide/installing-webots
There, you will find all the information about Webots and its installation.
Get the exercise files
[edit | edit source]If your version of Webots is 6.1.3 or more recent the curriculum is included in the Webots installation. You can find it in this directory:
(WEBOTS_HOME)/projects/samples/curriculum
Bluetooth Installation and Configuration
[edit | edit source]First of all, your computer needs a Bluetooth device to communicate with your e-puck. This kind of devices is often integrated in modern laptops. The installation of this device is out of the scope of this document. However, its correct installation is required. So, refer to its installation manual or to the website of its constructor. This document explains only the configuration of the Bluetooth connection between your computer and the e-puck. This connection emulates a serial connection. Refer to your corresponding operating system:
![]() First of all, your Linux operating system needs a recent kernel. Moreover, the following packets have to be installed: bluez-firmware, bluez-pin and bluez-utils[1]
First of all, your Linux operating system needs a recent kernel. Moreover, the following packets have to be installed: bluez-firmware, bluez-pin and bluez-utils[1]
The commands lsusb (or lspci according to your Bluetooth hardware) and hciconfig inform about the success of the installation.
Switch on your e-puck (with the ON-OFF switch) and execute the following command:
> hcitool scan Scanning ... 00:13:11:52:DE:A8 PowerBook G4 12" 08:00:17:2C:E0:88 e-puck_0202
The last line corresponds to your e-puck. It shows its MAC address (08:00:17:2C:E0:88) and its name (e-puck_0202). The number of the e-puck (0202) should correspond with its sticker.
Edit the /etc/bluetooth/hcid.conf and change the security parameter from ”auto” to ”user”.
Edit the /etc/bluetooth/rfcomm.conf configuration file and add the following entree (or modify the existing rfcomm0 entree):
rfcomm0 {
bind yes;
device 08:00:17:2C:E0:88;
channel 1;
comment "e-puck_0202";
}
rfcomm0 is the name of the connection. If more than one e-puck is used, enter as entrees (rfcomm0, rfcomm1, etc.) as there are robots. The device tag must correspond to the e-puck's MAC address and the comment tag must correspond to the e-puck name. rfcomm0 is the name this connection.
Execute the following commands:
> /etc/init.d/bluez-utils restart > rfcomm bind rfcomm0
A PIN (Personal Identification Number) will be asked to you (by bluez-pin) when trying to establish the connection. This PIN is a 4 digits number corresponding to the name (or ID) of your e-puck, i.e., if your e-puck is called "e-puck_0202", then, the PIN is 0202.
Your connection will be named "rfcomm0" in Webots.
![]() This part[2] was written using Windows XP. There are probably some differences with other versions of Windows.
This part[2] was written using Windows XP. There are probably some differences with other versions of Windows.
After the installation of your Bluetooth device, an icon named ”My Bluetooth Places” is appeared on your desktop. If it is not the case, right click on the Bluetooth icon in the system tray and select ”Start using Bluetooth”. Double-click on the ”My Bluetooth Places” icon. If you use ”My Bluetooth Places” for the first time, this action will open a wizard. Follow the instructions of this wizard up to arrive at the window depicted in the first figure of the wizard. If you already used ”My Bluetooth Places”, click on the ”Bluetooth Setup Wizard” item. This action will open this window.

In this first window, select the second item: ”I want to find a specific Bluetooth device and configure how this computer will use its services.”. Switch on your e-puck by using the ON/OFF switch. A green LED on the e-puck should be alight. Click on the Next button.
The second window searches all the visible Bluetooth devices. After a time, an icon representing your e-puck must appear. Select it and click on the Next button.

This action opens the security window. Here you have to choose four digits for securing the connection. Choose the same number as your e-puck (if your e-puck is called ”e-puck_0202”, choose 0202 as PIN) and click on the Initiate Paring button.

The opened window (on a figure too) enables you to choose which service you want to use. Select COM1 (add a tick). If there isn't any service, it's maybe because the battery is too low. This action opens a new window (see the next figure). Here you can select which port is used for the communication. Select for example ”COM6”.

To finish, click on the Finish button.

Finally, in the ”My Bluetooth Places” window (also shown on figure), right click on the ”e-puck_0202 COM1” icon and select the ”Connect” item.

Your connection will be named ”COM6” in Webots.
![]() If your Bluetooth device is correctly installed, a Bluetooth icon should appear in your System Preferences. Click on this icon and on the Paired Devices tab. Switch on your e-puck. A green LED on the e-puck should be alight. Then, click on the New... button. It should open a new window which scans the visible Bluetooth devices. After a while, the name of your e-puck should appear in this list. Select the e-puck in the list and click on the Pair button. A pass key is asked. It is the number of your e-puck coded on 4 digits. For example, if your e-puck has the number 43 on its stickers, the pass key is 0043. Enter the pass key and click on the OK button.
If your Bluetooth device is correctly installed, a Bluetooth icon should appear in your System Preferences. Click on this icon and on the Paired Devices tab. Switch on your e-puck. A green LED on the e-puck should be alight. Then, click on the New... button. It should open a new window which scans the visible Bluetooth devices. After a while, the name of your e-puck should appear in this list. Select the e-puck in the list and click on the Pair button. A pass key is asked. It is the number of your e-puck coded on 4 digits. For example, if your e-puck has the number 43 on its stickers, the pass key is 0043. Enter the pass key and click on the OK button.
Once pairing is completed, you need to specify a serial port to use in order to communicate with Webots. So, click the Serial Ports tab. Thanks to the New... button, create an outgoing port called COM1. Finally, quit the Bluetooth window.
Your connection will be named "COM1" in Webots.
Open Webots
[edit | edit source]This section explains how to launch Webots. Naturally it depends on your environment. So please refer to your corresponding operating system:
![]() Open a terminal and execute the following command:
Open a terminal and execute the following command:
> webots &
You should see the simulation window appear on the screen.
![]() From the Start menu, go to the Program Files | Cyberbotics menu and click on the Webots (+ version) menu item. You should see the simulation window appear on the screen.
From the Start menu, go to the Program Files | Cyberbotics menu and click on the Webots (+ version) menu item. You should see the simulation window appear on the screen.
![]() Open the directory in which you uncompressed the Webots package and double-click on the webots icon. You should see the simulation window appear on the screen.
Open the directory in which you uncompressed the Webots package and double-click on the webots icon. You should see the simulation window appear on the screen.
E-puck Prerequisites
[edit | edit source]An e-puck has a computer program (called firmware) embedded in its hardware. This program defines the behavior of the robot at startup.
There are three possible ways to use Webots and an e-puck:
- The simulation: By using the Webots libraries, you can write a program, compile it and run it in a virtual 3D environment.
- The remote-control session: You can write the same program, compile it as before and run it on the real e-puck through a Bluetooth connection.
- The cross-compilation: You can write the same program, cross-compile it for the e-puck processor and upload it on the real robot. In this case, the previous firmware is substituted by your program. In this case, your program is not dependent on Webots and can survive after the rebooting of the e-puck.
In the case of a remote-control session, your robot needs a specific firmware for having talks to Webots.
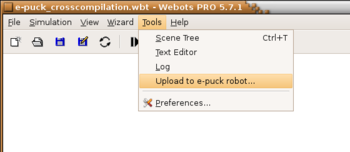
For uploading the latest firmware (or other programs) on the real e-puck, select the menu Tool | Upload to e-puck robot... as depicted in the figure. Then, a message box asks you to choose which Bluetooth connection you want to use. Select the connection which is linked to the e-puck and click on the Ok button. The orange LED on the e-puck will switch on. Then, a new message box asks you to choose which file you want to upload. Select the following file and click on the Ok button:
...webots_root/transfer/e-puck/firmware/firmware-X.Y.Z.hex
Where X.Y.Z is the version number of the firmware. Then, if the firmware (or an older version) isn't already installed on the e-puck, the e-puck must be reseted when the window depicted in the figure is displayed.