Cryptography/A Basic Public Key Example
The elementary working of Public Key Cryptography is best explained with an example. The working below covers the making of simple keys and the encryption and decryption of a sample of plain text. By necessity, the example is greatly simplified.
Basic Public Key Summary
[edit | edit source]- Public key encryption is used for internet secure links, such as when a browser opens a bank site or a site used with credit cards. Such addresses are prefixed by https as opposed to just http. RSA-OpenSSL is such an encryption system. An example of this secure site marking can be seen on the address of this page; this Wikibooks page (when the user is logged in) shows the https prefix or some alternative browser-specific marking that indicates that it is considered secure.
- Each site has an encryption key and a decryption key of its own, termed the public and private keys respectively. These are essentially very large numbers. These keys are always different, giving rise to the term asymmetrical encryption. In fact whenever we say key we mean a pair of numbers comprising the key; a key number to use in the raising of powers and another number that is the modulus of the arithmetic to be used for the work. For those unfamiliar with modular arithmetic, refer to the Wikibooks page High School Mathematics Extensions/Primes/Modular Arithmetic for a good, yet simple description.
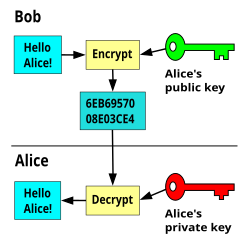
- Public keys are openly available for anybody to see, but private keys are not. The receiving site makes his public key available to the message sender, or by his making use of public directories. For each message transmission the sender uses this key to make the code. In this way only the private key of the recipient will decrypt it. A worked example has been provided in the text below, and the basic process can be seen in Figure 1.
- In fact, the two keys used for public key encryption form a reversible function. You could encrypt with the private key and decrypt with the public key if the system designers had otherwise intended it. Of course, for less public use the public keys could just as easily be treated as secret also. This reversible nature of the key pair is useful in testing digital certificates, where the issuer encrypts a certificate with his private key so that the recipient can then use his freely available public key to test its authenticity.
- The numbers used are made deliberately very large, and this makes the task of obtaining the private key from the public key too difficult for a hacker. It involves the factorization of very large numbers, and is very time consuming.
- Such systems, although imperfect, are nonetheless useful provided that the time to break them far exceeds the period for which the data is of any interest. The estimated time to break some such codes is many thousands of years.
- Signed digital certificates help certify the identity of user sites when delivering public keys. Browsers take steps to confirm their validity.
- The main advantage of the public key system is that there is a low administrative burden. Everything needed to send a message to a site is available in a public directory or is sent openly as a part of setting up the link.
- The main disadvantage of public key cryptography is that it is too slow for modern internet use. Because of this, the internet most often uses symmetric encryption for the main task; (a different method that uses a common key for both encryption and decryption); it simply uses public key methods to conceal the symmetric keys while they are being sent to the far end.
- There are several methods that hackers use to break coding:
- The brute force cracking of a key refers to trying every possible combination of private key while testing it against the relevant cyphertext. Such testing is time consuming, because a dictionary check or human intervention is needed at each iteration to decide whether or not plain language has emerged. Also, the numbers are very large, so this method is rarely of much interest.
- A mathematical attack refers to the finding of the two prime numbers, the product of which makes the modulus of the publicly available key. If these can be found then it simplifies the finding of the private key (more later); this method has the advantage that computers can be left to the task without much intervention. At the time of writing (2014) the record for breaking a key by mathematical attack is by Lenstra et al, on 12 December 2009, when an RSA-768 bit modulus (232 decimal digits) was factored using a method called the General Number Field Sieve (GNFS). The process required two years of collaboration and many hundreds of computing machines. (see: http://eprint.iacr.org/2010/006.pdf) Today most encryption keys in use are much bigger than the one that was broken, and a 1024 or 2048-bit key in an SSL certificate is still considered fairly safe against a mathematical attack. Note that the difficulty of breaking such a key increases exponentially with the key length.
- The history of successful intrusions has not involved code breaking however, but the hacking of the servers for their data and private keys. Other exploits have relied on the security omissions of individuals, or defective programming. For example, a recent SSL exploit, (2000-2014?), has involved accessing data, not by code breaking, but by a programming flaw that allows the sender to download blocks of memory content from the destination's server. The intention in SSL is to allow some text from the recipient's server to be returned as proof of message receipt and successful decryption. For this purpose the sender can specify the length of text to return, usually a header, and in any case less than 64Kbits in length. The core of the flaw was that if a very short message was sent but the sender asked for a larger block to be returned than was sent, the faulty program would oblige, so returning data that included other secure material from memory. Repeating this process every few seconds allowed a hacker to accumulate a large data block. The matter is stated to have been since corrected, but is said to have been available to any who knew of it for a period of about four years.
Making Site B's PUBLIC Key
[edit | edit source]A public key is available to all, and is used to encrypt messages that are being sent to the key's owner.
- Each site's computer produces two very large prime numbers, and since they are the basis of all that follows, these numbers are never revealed to any other. (Prime numbers are those that have no factors other than themselves or one).
- These two numbers are multiplied together to produce the modulus used in all of that site's calculations. The main public key is also derived from these primes, and determines the exponent to which the plain language numbers will be raised.
- This public key is available in directories and from certificate authorities, so when the SENDER wants to encrypt a message by public key cryptography he can easily use the recipient's public key (and modulus) to do it. Each site's public key set can be made to be almost certainly different from every other.
To illustrate the point for an intending recipient, let us make a simple example with the large prime numbers replaced with very small ones.
Say the two secretly held prime numbers are:
p = 5 , q = 11
Then the modulus of the arithmetic that will be used is given by their product:
m = 5 x 11 = 55 (the modulus of the arithmetic to use)
The encryption key can be found as follows: First, using the two prime numbers, calculate the function:
f(n) = (p-1) x (q-1) ∵ p = 5 and q = 11 ∴ f(n) = (5-1) x (11-1) ∴ f(n) = 40
then,
Select ANY number that is relatively prime to f(n) and less than it.
(Two numbers are said to be relatively prime when they share no common factors other than one. This term is also referred to as mutually prime, or coprime ).
The possible choices become: 3, 7, 9, 11, 13, 17, 19, 21, 23, 27, 29, 31, 33, 37, and 39. Say we select the public encrypt exponent = 7
The receiving site's PUBLIC key can then be safely given to the world as :
(7, 55) as (encryption exponent, modulus) (In practice the numbers would be very much larger)
The actual size of the numbers used is very large. For example, for a 1024-bit RSA encryption, this number is the size in bits of the modulus; this is equivalent to a decimal number of about 308 digits, or 256 hex digits. The public exponent most often chosen has an integer value of 65537. This exponent is chosen because it produces faster encryption than some other selections; that is, because of its large zero count in the binary form (10000000000000001), it lends itself to fast processing with binary shifting methods. It is known elsewhere as Fermat number F4. Despite this preference for the same exponent, recall that the other part of the public key set is the modulus, and that will differ between users based on the very large number of primes available.
Making Site B's Private KEY
[edit | edit source]Used by Site B when decrypting messages that were sent to them, encrypted using Site B's public key.
The private key pair is used to decrypt messages, and this key will only work if the public key of the same site was used to encrypt the message. That is to say, Site B's public key is obtained from a directory, then used by Site A to encrypt a message for them. When the message gets to Site B, Site B uses its own private key for decryption.
Continuing with the simple example above, the private key of Site B is made from its public key as follows.
private decrypt exponent = (public encrypt exponent)-1 Mod f(n)
∵ public encrypt exponent = 7 , and f(n) = 40
∴ (private decrypt exponent x 7) Mod 40 = 1
∴ private decrypt exponent = 23
The Site B PRIVATE key pair is then:
(23,55) as (decryption exponent, modulus)
It will have been noted by some that the same number can result for both the encrypt and decrypt exponents. This particular case must be avoided by deliberate testing since a hacker would likely test for this possibility early in the process of an attack. In the above examples, this would have been the case if 9, 11, 21, 33 or 39 were chosen for the public key instead of some other. Lest it be thought that anticipation of this error is simple, notice that even in this set that both coprimes that are themselves prime (eg; leading to: 11 * 11 = 1 mod 40), and those that are coprime but not in themselves prime (eg; 9, 21, 33, and 39), can all produce this insecure state of affairs.
With the use of long primes, m the modulus (their product), is very much longer, but it should be apparent that an intending hacker could still obtain the private key if he were able to find the two secret primes as a starting point. Both the public key and the modulus to use with it are given to all who require it for encryption, so the burden of a mathematical attack reduces to the difficulty of factoring the modulus into these two secret primes. For the simple example shown above (m=55) this task is very simple, but for a very large number this effort is prohibitively long.
The native format in which the private key is delivered is in fact base-64, (a character set that needs only 6 bits per character, instead of the 4 for hex or the 7 for ASCI character codes). Unlike the public key string, the layout of a practical private key string for a 1024-bit RSA encryption contains the private key details, the public key details, and the secret numbers used in their making, as well as various other numbers and headers. The private key exponent, unlike the public exponent, is quite long, and is the equivalent of 256 hex digits in length. The secret primes are each 128 hex numbers in length. The decimal equivalent lengths are 308 digits for the private exponent (and the modulus), and 154 digits for each of the secret numbers.
Factoring the Modulus
[edit | edit source] number of primes ≅ x/(logx - 1)
now a 64 bit space is equivalent to about 20 digits
∴ number of primes ≅ 4 * 1017
then assuming 1 million calculations per second, (a wildly optimistic assumption for most):
the time to test all the primes ≅ 13,500 years
The example here was limited to 64 bits because the more representative figures, 128, 256, 512, 1024, and 2048-bit calculations are too big for most calculators. See The Math Behind Estimations to Break a 2048-bit Certificate by DigiCert for more details.
This example does not consider the use of improved methods for factoring, and these appear frequently in the literature. At present, (2014), the best of these is considered to be the General Number Field Sieve (GNFS), used to establish the record in December 2009.
To expand a little on the subject of improved methods, it will be apparent that starting with lists of tabulated primes speeds up the process. This, and the production of calculated product tables against their future need also allows much faster processing than would otherwise be possible by calculating on the fly. Because clearly, for a large set of such cracking problems, half of the solutions will lie in the first half of the trial values and half of them in the second, it has become the habit to express the expected time to solution for half of the set as opposed to the whole number implied by the Prime Number Theorem.
Encryption with B's Public Key
[edit | edit source]Assume that the public key pair belong to a Site B. Assume also that a plain language character represented by the number '2' is to be encrypted by Site A and sent to the recipient Site B: Site A uses Site B's public key pair to do so.
Assume plaintext=2
cyphertext = plaintext public encrypt exponent Mod n
∵ public encrypt exponent =7, and modulus = 55
∴ cyphertext = 27 Mod 55 = 128 Mod 55
∴ cyphertext = 18
With the very small numbers used in the example the cracking of the code would be relatively simple. But for very large values of primes p and q, and without knowing the private key value, the burden becomes very difficult. In some cases the task would involve an unreasonable time even for a very large number of computers.
Public key encryption does not disguise the relative frequency of the characters used. This is considered a failing in such systems since it improves the chances of cracking the code. So, the plaintext characters are arranged into groups before encryption to hide their natural frequencies of use; the groups are very large, the limit being that the size of a number encrypted must be smaller than the modulus in use.
Decryption with B's Private Key
[edit | edit source]Decryption using the above specific example is acheived as follows: For the received cyphertext = 18
With cyphertext=18 from previous section
Plaintext = cyphertextprivate decrypt exponent Mod n
∵ private decrypt exponent = 23, and modulus = 55
∴ Plaintext = 1823 Mod 55 = 74347713614021927913318776832 Mod 55
∴ Plaintext = 2 (You can only just confirm this with the Windows scientific calculator)
Notice that the plain language value of 2 has been recovered, which is the required result.
Exceptions
[edit | edit source]Some attempts with other than the correct private key will be nonetheless successful. There are exceptions that need to be considered. For example, in the above case, using the decrypt exponent =3 will also produce the correct result. See below:
With cyphertext=18 from previous section
Plaintext = cyphertextprivate decrypt exponent Mod n
∵ hacker's attempted decrypt exponent = 3, and modulus = 55
∴ Plaintext = 183 Mod 55 = 5832 Mod 55
∴ Plaintext = 2 also the right result.
Note that every (N^7Mod55)^3Mod55 == (N^7Mod55)^23Mod55)
In a practical environment further consideration would be given to such matters in the selection of keys.
The Internet Speed Compromise
[edit | edit source]Because public key encryption and decryption is so very slow, it is unsuitable in its native form for internet use. In fact, asymmetric public key encryption is used for only a small part of internet communications. Such systems are hybrid. The summary of the method used is as follows:
- The text to be transmitted securely will be encrypted, not by public key cryptography, but by using SYMMETRIC key encryption. This is typically a 128 bit cipher, but can be greater. Symmetric key methods need both sites to use the same key. To do this one site must at some stage originate the key then send a copy of it to the other.
- This SYMMETRIC key, is not sent to the far end openly but is kept safe by first encrypting it using PUBLIC key methods. The public key of the destination site is used for this.
- The recipient uses his PRIVATE key to decrypt this cyphertext, and to recover the SYMMETRIC key value. He then decrypts the main symmetric ciphertext with it.
- The symmetric encryption key is discarded at the end of the current session, and the asymmetric public key may or may not be discarded, depending on the system in use. A short lifetime for the key reduces the chances of a successful key recovery during cyber-attacks and the subsequent decoding of recorded traffic at a later date. With this in mind, it might be that short sessions are more secure than long ones, provided of course that discarded means the complete removal from memory, and not just the ubiquitous delete.
The systems currently in use for internet browsers are Transport Layer Security (TLS) and its predecessor, Secure Sockets Layer (SSL). A complete description of these is available at Wikipedia's Secure Sockets Layer.
Note that in a duplex system, that is, the usual kind that sends in both directions, there will be two such procedures. One originated at each end. The key sets used for send and receive, for both asymmetric and symmetric encryption systems are all different.
Message Authentication
[edit | edit source]Security breaks down if outsiders can change the message in transit, or if they mis-represent themselves right from the start. In an attempt to overcome these risks digital certificates were devised. In a further attempt to ensure that the certificates were from the place respected by the users, the certificates were given digital signatures. One such method among many is the Digital Signature Algorithm (DSA), the basis of the Digital Signature Standard (DSS).
These certificates are not just simple text messages, which of course could be imitated, but use calculated values based on the content of a message. The entire basis of certification depends both on the designed properties of these hash algorithms and on the integrity of those who assert their worth. Their properties include:
- Sensitivity: They are very sensitive. A very small change in a hash algorithm's input always creates a very large change in its output value.
- Specificity: They are very specific. Although it depends on the hash algorithm used, there is very little chance that two different inputs could ever produce the same output. When this happens, say once in many billions, it is referred to as a collision.
- Opacity: An input value cannot be found from a output value. This is because of the great complexity of the algorithm and in particular, because of the liberal use of modular arithmetic's one-way functions.
- Secrecy: Some hash algorithms are available for public use, but proprietary interests can make their own. Algorithms available for the use of most include MD5, SHA1, SHA2, SHA3, and others. MD5 has been broken. SHA1, the basis for much of the current certification, is deprecated in its use for more complexity.
The hash value is calculated by the sender and compared with one calculated at the receiving end, where the two must match for acceptance. Like encryption itself, hash values are too laborious to reverse engineer, that is to say, new or changed messages could not be made by outsiders to represent an existing hash value within any useful time period. Because of this they provide a basis upon which to verify that a message's contents were not changed since the certificate was issued.
Certificates themselves are tested against known root certificates within the browser store, to ensure that the certificates are from a known reliable source. If certificates are secret-signed with a private key known only to the issuing authority, then validation of the certificate can be made by decrypting the signature with its public key. That is to say, because the process is reversible, validation of the source can be made.
The actual process used for these tasks is more complex than is implied in summary, involving many long-bit calculations, but the strength of the system is unlikely to satisfy the skeptical until the sums are seen. Refer to the pdf file How Encryption and Digital Signatures Work and read the section An Example of a Digital Signature Mechanism for such a description.
The process of testing certificates and other matters are in any case summarized by browsers for their users. Browsers will indicate clearly whether or not they consider a connection to be secure. The most common of these indications includes an added padlock somewhere on the screen and the modification of the site's http address heading to read https. Some browsers such as Opera add other information such as color coding to represent the levels of security.
See also
[edit | edit source]- High School Mathematics Extensions/Primes/Modular Arithmetic : The stuff you may have forgotten.
Further reading
[edit | edit source]- Bionic Buffalo Tech Note 35: How Encryption and Digital Signatures Work Clearly describes the working of the Data Encryption Standard (DES), the RSA Public Key Standard, and the Digital Signature Algorithm (DSA), with generous math notes.
- Digital Signature Algorithm
- Code Breaking Factoring Record : The Math Behind Estimations to Break a 2048-bit Certificate by DigiCert.
- RSA Factoring Challenge: Contains tables of the progress so far in prime factoring.
- The RSA Key Layout: A page showing the precise layout of both private and public keys for a 1024-bit RSA encryption.