Computer Systems Engineering/Reliability models
What is a system?
[edit | edit source]Definition
[edit | edit source]A system is a combination of elements forming a unitary whole.
Examples
[edit | edit source]- River or transportation system
- System of currency
- Comprehensive assemblage of facts, principles, and doctrines in a particular field
- System of marking, numbering, measuring, etc.
- University of South Carolina – composed of the main campus in Columbia and many branch campuses
- Computer (our main interest) – includes components: memory, processor, motherboard, disk, printer, wireless adapter, etc.
Every set is not a system. In order to be a system, a set needs a sense of unity, functional relationships between its components, and/or some useful purpose. For example, a random group of items in a room would not be a system unless one of the above conditions are met.
The elements of a system are as follows
[edit | edit source]- Components: operating parts for input processing or output
- Attributes: properties of the components that characterize the system
- Relationships: links between components and attributes
Components are interrelated and work together toward some purpose, objective, or function. The properties and behavior of each component affect the properties of the system as a whole. For example, the speed of computer memory, the disk access time, and its capacity will all affect the overall speed of a computer. The properties of each component depend on at least one other component. For example, memory performance depends on bus speed (bandwidth). Each subset (or subsystem) of components are related in the same manner, but the system cannot be divided into independent subsets.
Often, a system has a hierarchy of components. A system is made up of components, and those components are made up of smaller components. The lower hierarchical levels are called subsystems. One example is a hard disk drive. The drive is a component of a computer, but it has multiple platters, a read/write head, a buffer, and many more smaller components.
Systems can be classified as
[edit | edit source]- Natural and man-made (human-made)
- Physical and conceptual
- Static and dynamic
- Closed and open
Engineering is concerned with the economical use of limited resources in order to benefit people. This is accomplished by approaching a problem with several things in mind. In the domain of systems engineering, it is necessary to define product and system requirements as they relate to true customer needs. For example, designing an email system to meet a customer’s communication needs must be well-defined to meet those needs. Engineering also must address total systems, with all elements, from a life-cycle perspective. The overall hierarchy must be considered, including the interactions between various levels and elements at the same level. An example of this in a computer system is the memory hierarchy, composed of a 2-level cache, main memory, and virtual memory on a hard disk. It is often necessary to organize various related disciplines into one engineering effort in a timely, concurrent manner, such as separate mechanical and electrical aspects of a system. Finally, it is vital to establish a disciplined approach to a process (manage a process to get results). This includes appropriate review, evaluation, and feedback to ensure orderly and efficient progress.
A system’s life cycle is composed of the following
[edit | edit source]An example of this process in application is as follows. Dictators in third-world countries often want to ride around in fancy cars. However, there is not much support for this preference. Filling stations are not very ubiquitous, and the economy may not support many trained mechanics for automotive repairs. So, from an engineering standpoint, this system would require much more design and money to make it viable.
Summary of Systems Engineering
[edit | edit source]- Top-down: look at the system as a whole
- Life-cycle orientation
1. Design, development production/construction, distribution, operation, maintenance & support, retirement, phaseout, disposal 2. Past emphasis on design & acquisition, with little emphasis on production, operation, maintenance, support & disposal 3. Example: If an old computer goes to a landfill (taking up space and polluting the groundwater), a better design would allow the recovery of gold, lead, and other materials upon disposal.
- Better definition of system requirements - Trace down customer needs to individual components
- Interdisciplinary
1. Systems usually require multiple disciplines 2. Example: In the development of a computer game, a company has 3 employees – an artist, a musician, & a programmer.
Reliability
[edit | edit source]Definition
[edit | edit source]“Reliability is the probability of a device performing adequately for the period of time intended under the operating conditions encountered.” – NASA
Math Model of System Reliability
[edit | edit source]Reliability, R(t), is the probability of a system not failing during the period [0,t].
Experiment
[edit | edit source]Test a large number of systems.
Hazard function, h(t):
Separate variables and integrate:
Summary F(t) is the failure distribution function R(t) = 1-F(t) is the reliability f(t) is the failure density function h(t) is the hazard function
The difference between f(t), h(t):
At time 2 to 3:
Hazard Function
[edit | edit source]The shape of the hazard function indicates how an item ages. It has an intuitive interpretation as the amount of risk an item is subject to at a time t:
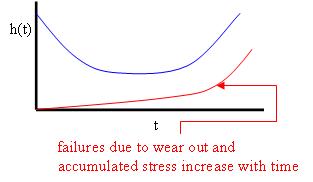
Increasing Hazard Function This is probably the most likely situation, because items wear out or degrade with time. For example, look at mechanical items that undergo wear or fatigue, such as the rubber getting thinner on car tires over time.
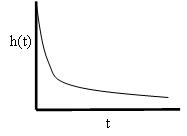
Decreasing Hazard Function In this situation, an item improves; that is, an item is less likely to fail as time passes. For example, some metals “work-harden” through continued use. Also, software may improve as bugs are removed.
Bathtub Shaped Failure Rate This situation describes many natural systems and manufactured goods. It is a composite of 3 effects:
*early failures due to defects *late failures due to wear out *accidents at a constant rate
Human Life Characteristics
MTTF = 800 years corresponds to a failure rate of
or 5 deaths in a population of 4000 in 1 year
Exponential Reliability Distribution
[edit | edit source]Recall:
This distribution is the most used reliability model. It is valid for many electronic components over most of their lifetimes, and is the basis for MIL-HDBK-217.
Memoryless Property
[edit | edit source]Let T = item lifetime (R.V.)
This is the conditional probability that a failure distribution for an item that has survived to time s is identical to a brand new item.
One example of this is a fuse. A fuse fails due to a power surge, but does not weaken or degrade over time. The memoryless property, with its used-as-good-as-new assumption, is restricted in applicability. An exponential distribution is easily misapplied for the sake of simplicity:
*statistical techniques are particularly tractable *can add failure rates *field data often allow an estimation of only this one-parameter distribution
C provides a quick check of a data set for exponentiality
Weibull Distribution
[edit | edit source]Waloddi Weibull, a Swedish physicist, introduced this distribution in 1939. It is a generalization of an exponential distribution suitable for modeling lifetimes having constant, strictly increasing, and strictly decreasing hazard functions.
Note that the Weibull Distribution can match different phases of the bathtub curve.
Procedure: 1. Collect the failure data. 2. Get the best fit for the data to a Weibull distribution:
If item is still in the burn-in phase
*Improve supplier quality *Burn in the system longer *Be more careful while manufacturing
At GE, light bulbs with as little as a 1% variation in their filaments lead to a 25% shorter lifespan.
If attributed to random failures (accidents)
*Make stronger components *Derate – use components at less than the rated value *Use newer technology (i.e. software control, longer-life transistors instead of vacuum tubes, etc.) *Make components less environmentally sensitive (i.e. better packaging) *NPN transistors < PNP transistors
For example, halogen and compact fluorescent bulbs use a different technology to extend life. Further, rating of incandescent long-life light bulbs may proceed as follows:
If item is in the wear-out region
*Use stronger, longer-lived components *Use newer technology, etc. *Use a different architecture
Measures of System Reliability
[edit | edit source]Mean Time To Failure (MTTF) This means that only about 37% of items survive more than 1 MTTF. However, this distribution has a very long tail:
Repairable Systems
[edit | edit source]Mean Time To Repair (MTTR)
Mean Time Between Failures (MTBF)
Note that MTBF and MTTF are often used almost interchangeably by some authors.
Steady State Availability
[edit | edit source]For example, if a system has only 15 minutes of downtime in a 2-year period, then
Reliability Models
[edit | edit source]For a series system:
The system works if A works and B works and C works and D works.
For example, if
In terms of time,
Suppose that
Observe that for the constant failure rate (exponential) model, a Weibull distribution can be used:
but this is much more difficult.
Redundancy
[edit | edit source]- Very simple
- Very appealing
- Very deceptive
Component reliability = .9
The system works if either component works or fails if both fail. R = 1-P(fail)
= 1-P(first fails & second fails) = 1-P(first fails)P(second fails) = 1-P(.1)(.1) note independence = .99
Example: Light Bulbs
Series System:
Parallel System:
Uses of Redundancy
[edit | edit source]- To increase reliability, availability
- To eliminate single points of failure
Important in military systems Becoming important in commercial systems Important in high availability systems in which the part being repaired must be shut down
- Degradable fault tolerance
Another Example
Probability of system failure = (Probability of A failing) AND (Probability of B failing)
Observe that this is not exponential.
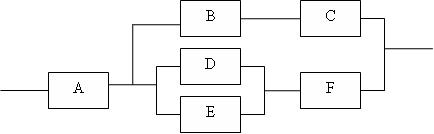
Combined Series-Parallel Systems
[edit | edit source]Series-Parallel System Reduction
[edit | edit source]Combine series or parallel component reliabilities to give an equivalent reliability and reduce the system. See the following examples:
1) reduce D, E
2) reduce B, C and I, F
3) reduce II, III
Examine the two different configurations of the following 4-component system with identical components. The component failure rate is:
Moral:
We get the greatest gain in reliability by making a system redundant at the lowest level possible. Generally, it is better to make modules redundant than to duplicate the system.
System Design
[edit | edit source]Make modules redundant in order to achieve reliability goals.
Example: AM Signal Pickup
Series system:
Redundant Design I Series-Parallel at component level:
Functional parameter will change if a component fails – probably.
Redundant Design II Parallel Series
Combine Outputs:
Interfaces between parallel subsystems increase complexity of design (which decreases reliability).
Estimating Reliability
[edit | edit source]The Parts Count reliability model assumes that the system is in series; this model underestimates the reliability of redundant systems. For redundant systems, the Parts Count model is used to estimate the reliability of the series subsystems and interfaces. Reliability is then computed while considering the redundancy structure.
Using our AM Signal Pickup example again:
Ground Mobile environment (GM)
Series Subsystem:
Interface :
System Reliability Estimate:
Simplex System:
Simple Redundant System (ignoring interface problem):
R = .9876
Note: In some cases the interface reliability may dominate the redundant subsystem reliability and determine the overall system reliability. In this case the simplex system may be more reliable than the redundant system.
Non-Series/Parallel System Reduction
[edit | edit source]Use decomposition:
- Find the keystone component and partition the system according to whether the keystone component is good or bad.
- The keystone component binds together the reliability structure of the system.
Law of Total Probability
Example:
Choose A as the keystone component.
If A is good:
Series/Parallel System
If A is bad:
Series System
Convenient Notation
Notes:
- If the “wrong” keystone component is chosen, the component decomposition technique works, but reduction is not as extensive.
- New keystone components can be repeatedly chosen to further reduce a subsystem.
Parallel Redundancy
[edit | edit source]This system works as long as 1 module works.
M-out-of-N System Reliability
This system works if at least M modules work.
It can tolerate up to N-M failures, so
Voting Systems
[edit | edit source]The Voter compares the outputs of all N modules and outputs the majority. This is called N Modular Redundancy (NMR). The NMR system will generally have an odd number of modules, so . The system works if (n+1) modules are working (it can have up to n failures), and if the voter is working.
Simple Voter
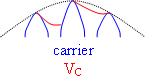
Analog Signal or Numeric Voting
The voter compares input signals (or numeric values) and picks the middle value as its output. Normal operation is as follows:
However, error conditions may arise:
Note: Reliability calculations assume the worst case conditions:
- All modules fail in the same logical direction
- There are no compensating failures (i.e. one module becomes stuck at 1, while another is stuck at 0)
Triple Modular Redundancy (TMR)
[edit | edit source]Example:
Comparison of NMR System Reliabilities
Measure time in units of MTTF.
The following figure depicts the reliability of an NMR system for increasing N:
Observe:
Extra hardware increases reliability for the short term but once redundancy is used up there is simply more hardware to fail and reliability decreases quickly.
For a TMR system:
For redundant systems MTTF may not be an appropriate measure of reliability. It is necessary to look at R(t) in relation to mission time.
Cascading TMR
[edit | edit source]A voter gives a simple point of failure, so a design may triplicate the voter (TMR).
System reliability is determined by 3 parallel modules in the first stage, a voter in the last stage, and a parallel voter-module in the intermediate stage.
NMR Systems
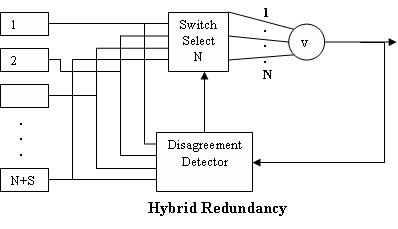
[edit | edit source]Failed modules accumulate in an NMR system until they become the majority and the system fails. The system life can be extended by purging all of the failed modules. This can be accomplished through Hybrid Redundancy (using spares), or through Adaptive Voting (also called Change Voting). In essence, the failed module(s) must be detected first.
This system has the following attributes:
- N+S modules (S spares)
- Disagreement Detector compares the voted output with the module outputs
- Switch selects the outputs from N modules to give to the voter
- If a module fails, the Disagreement Detector tells the switch to replace the failed module with a spare one
This configuration is often used with TMR systems. If more than a few spares are switched, the complexity increases to a point where its reliability dominates the system reliability.
N-ary Programming (TMR)
[edit | edit source]Say we have 3 programmers write code and then vote on the results. In a TMR system, each program could execute on a completely different set of hardware. However, software is labor-intensive and very expensive to produce. N-ary programming significantly increases this cost, does not protect against specification errors, and introduces timing and coordination problems since each of the programs is not identical to the others.
Adaptive Voting
[edit | edit source]In adaptive voting, the voted output is compared with the module outputs. When a module fails, it is removed along with one other module (this is to keep an odd number of modules). The voter is then changed to select the majority of the remaining modules. This approach can be combined with hybrid redundancy in order to switch good modules back in. Voting (particularly TMR) is used in many fault-tolerant, very-high-reliability computer systems.
Standby Redundancy
[edit | edit source]- Operate with A
- Switch to B when A fails
- A and B are not independent
In general, A and B can be different (i.e. A can be an on-line power source while B can be a generator). It should be noted that B can fail while in its standby mode, or the switch could fail. Examine the following simple case. Assume:
Reliability is as follows:
Recall that the above is the law of total probability.
Therefore,
A sequence of failures forms a process that starts over each time a device fails and a new one is switched in. This is called a renewal process. The time between failures is exponentially distributed, where X is a random variable denoting the time between failures. Suppose we have n systems as follows:
Recall that for a Poisson process, i) Events in non-overlapping intervals are independent ii) P(event in small interval h) = P(no event in h) = iii) The time between events, X, is exponentially distributed, iv) The number of events in an interval T,n(T) has the Poisson distribution .
Also recall (for iii) that
Furthermore,
As you might have deduced, this sequence of failures is a Poisson process. Therefore,
For an n component system:
As an overview, compare the following for 2 units:
- Standby Redundancy:
- Parallel Redundancy:
- Simplex System:
- Standby Redundancy:
- Parallel Redundancy:
- Simplex System: R = p