Commutative Algebra/Functors, natural transformations, universal arrows
Functors
[edit | edit source]Definitions
[edit | edit source]There are two types of functors, covariant functors and contravariant functors. Often, a covariant functor is simply called a functor.
Definition 2.1:
Let be two categories. A covariant functor associates
- to each object of an object of , and
- to each morphism in a morphism ,
such that the following rules are satisfied:
- For all objects of we have , and
- for all morphisms and of we have .
Definition 2.2:
Let be two categories. A contravariant functor associates
- to each object of an object of , and
- to each morphism in a morphism ,
such that the following rules are satisfied:
- For all objects of we have , and
- for all morphisms and of we have .
Forgetful functors
[edit | edit source]I'm not sure if there is a precise definition of a forgetful functor, but in fact, believe it or not, the notion is easily explained in terms of a few examples.
Example 2.3:
Consider the category of groups with homomorphisms as morphisms. We may define a functor sending each group to it's underlying set and each homomorphism to itself as a function. This is a functor from the category of groups to the category of sets. Since the target objects of that functor lack the group structure, the group structure has been forgotten, and hence we are dealing with a forgetful functor here.
Example 2.4:
Consider the category of rings. Remember that each ring is an Abelian group with respect to addition. Hence, we may define a functor from the category of rings to the category of groups, sending each ring to the underlying group. This is also a forgetful functor; one which forgets the multiplication of the ring.
Natural transformations
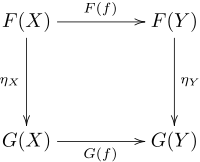
[edit | edit source]Definition 2.5:
Let be categories, and let be two functors. A natural transformation is a family of morphisms in , where ranges over all objects of , that are compatible with the images of morphisms of by the functors and ; that is, the following diagram commutes:
Example 2.6:
Let be the category of all fields and the category of all rings. We define a functor
as follows: Each object of shall be sent to the ring consisting of addition and multiplication inherited from the field, and whose underlying set are the elements
- ,
where is the unit of the field . Any morphism of fields shall be mapped to the restriction ; note that this is well-defined (that is, maps to the object associated to under the functor ), since both
and
- ,
where is the unit of the field .
We further define a functor
- ,
sending each field to its associated prime field , seen as a ring, and again restricting morphisms, that is sending each morphism to (this is well-defined by the same computations as above and noting that , being a field morphism, maps inverses to inverses).
In this setting, the maps
- ,
given by inclusion, form a natural transformation from to ; this follows from checking the commutative diagram directly.
Universal arrows
[edit | edit source]Definition 2.7 (universal arrows):
Let be categories, let be a functor, let be an object of . A universal arrow is a morphism , where is a fixed object of , such that for any other object of and morphism there exists a unique morphism such that the diagram
commutes.