Circuit Theory/Two Port Networks
One of the most useful circuits in existence is the amplifier. They are found in almost every electronic device, from radios and TVs to washing machines and oscilloscopes. They form the basis of nearly all more complex circuits. An amplifier is a device that takes an input and gives a proportional (but not necessarily larger) output. We can represent this as a two-port circuit, which has an input port and an output port.
Firstly, let us consider the one-port circuit with which we have already become familiar:

Basic circuit elements such as resistors, capacitors, inductors and independent sources form the most elementary kind of one-port circuits. More generally, a one-port circuit can have any number of passive elements, independent and dependent sources and nodes. Often, once one of these circuits has been designed, we are no longer interested in how it works, and are happy to represent it by its behavior at its port. By using techniques we have already learned, we can reduce it to a Thévenin or Norton equivalent circuit.
Now, consider the two-port circuit below:

Some devices have more than two terminals, for example BJTs with three and MOSFETs with three or four. In these cases, it is impossible to represent them as one-port circuits, and two-port circuits are the only option. Two-port circuits have the same application as one-port circuits, in that, they allow us to consider only the behavior of a circuit and not unnecessary internal detail.
Review of One-Port Circuits
[edit | edit source]In this section, we will look at one-port circuits again and consider a more systemic way of finding the Norton and Thévenin equivalent circuits.
Example 1
[edit | edit source]Consider the following circuit:

Let us compute the Thévenin and Norton equivalent circuits looking into the port consisting of nodes and of this circuit. To find the open-circuit voltage, we find the current flowing through the 1/3 Ω resistor using the current-divider rule and multiply by 1/3:
The equivalent resistance is found by deactivating the current source and finding the resulting impedance:
The short-circuit current can be found as follows:
Hence, we have the following Thévenin and Norton equivalent circuits:
Thévenin and Norton circuits are simplifications of the original circuit: however many nodes the original circuit has, the equivalent circuits have just two (here, 0 and 1). We can think of this process as a process of elimination of nodes that are not port terminals (in this case node 2). We can use the systematic method of nodal analysis to achieve this.
To do this, we define node 0 as our reference and place a test current source between nodes 0 and 1:
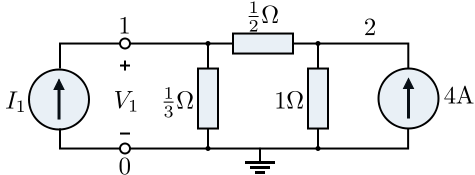
We can now perform by-inspection nodal analysis:
Node 2 is not a port node and therefore must be eliminated. We can use Gaussian elimination to do this. Pivot about the "3":
This resulting equation may be expressed in either current or voltage forms:
It is clear that these correspond to the Thévenin and Norton equivalents we found previously. If the circuit does not have independent sources, we will merely get a expression corresponding to a single resistance.
Example 2
[edit | edit source]Let us now consider the slightly more complex example below:










