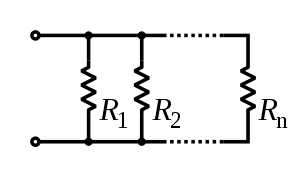
Resistors in parallel share the same voltage. They split the current up. Giving the current multiple paths to follow means that the overall resistance decreases.
A diagram of several resistors, side by side, both leads of each connected to the same wires.
R
t
o
t
a
l
=
1
1
R
1
+
1
R
2
+
⋯
+
1
R
n
=
1
∑
1
R
i
{\displaystyle R_{\mathrm {total} }={\frac {1}{{\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+\cdots +{\frac {1}{R_{n}}}}}={\frac {1}{\sum {\frac {1}{R_{i}}}}}}
The above equation is often called the "one over -- one over" equation.
used to show how impedance add's in parallel A group of parallel branches split up the current, but share the same voltage. The parallel branches connect the same two nodes.
The impedance of parallel branches can be combined into one impedance.
Consider these parallel branches: one with a resistor, another with a capacitor and a third with an inductor.
Now drive them with a voltage source:
V
s
=
10
∗
c
o
s
(
22400
t
+
30
∘
)
{\displaystyle V_{s}=10*cos(22400t+30^{\circ })}
V
s
=
10
∗
e
−
5000
t
c
o
s
(
22400
t
+
30
∘
)
{\displaystyle V_{s}=10*e^{-5000t}cos(22400t+30^{\circ })}
There is just one current,
V
{\displaystyle V}
the impedance symbol is .. a box Parallel Impedance calculation with matlab ..m-file The terminal equations are:
V
s
=
I
r
∗
R
{\displaystyle \mathbb {V} _{s}=\mathbb {I} _{r}*R}
V
s
=
I
L
∗
j
ω
L
{\displaystyle \mathbb {V} _{s}=\mathbb {I} _{L}*j\omega L}
V
s
=
I
L
∗
s
L
{\displaystyle \mathbb {V} _{s}=\mathbb {I} _{L}*sL}
I
c
=
V
s
∗
j
ω
C
{\displaystyle \mathbb {I} _{c}=\mathbb {V} _{s}*j\omega C}
I
c
=
V
s
∗
s
C
{\displaystyle \mathbb {I} _{c}=\mathbb {V} _{s}*sC}
There are no loop equations and the junction equation is:
I
r
+
I
L
+
I
c
−
I
s
=
0
{\displaystyle \mathbb {I} _{r}+\mathbb {I} _{L}+\mathbb {I} _{c}-\mathbb {I} _{s}=0}
Solving the terminal equation for currents, substituting and dividing both sides by
V
s
{\displaystyle \mathbb {V} _{s}}
I
s
V
s
=
1
R
+
1
j
ω
L
+
j
ω
C
{\displaystyle {\frac {\mathbb {I} _{s}}{\mathbb {V} _{s}}}={\frac {1}{R}}+{\frac {1}{j\omega L}}+j\omega C}
I
s
V
s
=
1
R
+
1
s
L
+
s
C
{\displaystyle {\frac {\mathbb {I} _{s}}{\mathbb {V} _{s}}}={\frac {1}{R}}+{\frac {1}{sL}}+sC}
In terms of impedance, if:
1
Z
=
1
R
+
1
j
ω
L
+
j
ω
C
{\displaystyle {\frac {1}{Z}}={\frac {1}{R}}+{\frac {1}{j\omega L}}+j\omega C}
1
Z
=
1
R
+
1
s
L
+
s
C
{\displaystyle {\frac {1}{Z}}={\frac {1}{R}}+{\frac {1}{sL}}+sC}
Then:
I
s
V
s
=
1
Z
{\displaystyle {\frac {\mathbb {I} _{s}}{\mathbb {V} _{s}}}={\frac {1}{Z}}}
In general, impedances add in series like resistors do in the time domain:
1
Z
=
∑
1
R
i
+
∑
1
j
ω
L
i
+
∑
j
ω
C
i
{\displaystyle {\frac {1}{Z}}=\sum {\frac {1}{R_{i}}}+\sum {\frac {1}{j\omega L_{i}}}+\sum j\omega C_{i}}
1
Z
=
∑
1
R
i
+
∑
1
s
L
i
+
∑
s
C
i
{\displaystyle {\frac {1}{Z}}=\sum {\frac {1}{R_{i}}}+\sum {\frac {1}{sL_{i}}}+\sum sC_{i}}
or
Z
=
1
∑
1
R
i
+
∑
1
j
ω
L
i
+
∑
j
ω
C
i
{\displaystyle Z={\frac {1}{\sum {\frac {1}{R_{i}}}+\sum {\frac {1}{j\omega L_{i}}}+\sum j\omega C_{i}}}}
Z
=
1
∑
1
R
i
+
∑
1
s
L
i
+
∑
s
C
i
{\displaystyle Z={\frac {1}{\sum {\frac {1}{R_{i}}}+\sum {\frac {1}{sL_{i}}}+\sum sC_{i}}}}
Z
=
99.9938
−
0.7857
i
=
99.9969
∠
−
0.0079
(
−
0.4502
∘
)
{\displaystyle Z=99.9938-0.7857i=99.9969\angle -0.0079(-0.4502^{\circ })}
Z
=
186.85
−
837.07
i
=
857.6701
∠
−
1.3512
(
−
77.4170
∘
)
{\displaystyle Z=186.85-837.07i=857.6701\angle -1.3512(-77.4170^{\circ })}
So the exact same components hooked in series are dominated by the inductor (large reactance of the inductor overshadows the smaller reactance of the capacitor), but when the same components are hooked in parallel, the small er capacitive reactance dominates.
What is the point of all this? The goal is to start with simple circuits, explore them with words and symbols, find the patterns and generalize, establish and name concepts and then wait for their application. What are we waiting for? Selecting channels on a TV/Radio/Wifi, ZigBee, RFID , Cellphones, Blue Tooth and sending data over these channels as well as to hard drives and SD cards, monitors and hubs, designing antennas, ....