Circuit Theory/Node Analysis
Node analysis is done in the phasor domain.
The Node Analysis method reduces the number of equations and unknowns one is finding in a circuit.
Kirchhoff's method finds all currents and voltages. Node Analysis only finds the voltages at nodes (junctions).
Node analysis starts with Kirchhoff junction equations:
and solves terminal equations so that current is a function of voltage, and then substitutes into the junction current equation:
What is ? It is the voltage with respect to ground of the node on either side of the device being considered.
Where current is following from node_A to node_B.
At first glance this may seem trivial, but there are subtle differences exposed when doing the problems:
- Node voltages are relative to ground. They are not Kirchhoff's drops across individual devices.
- Assume all currents leave nodes.
- Terminal relation equations are more complicated.
- Has to be done in the phasor domain so impedances between nodes can be computed.
- Can have too few equations requiring finding "super node" equations.
- Some problems can not be solved. Recognizing these is not trivial.
Examples
[edit | edit source]Basic case
[edit | edit source]
The only unknown voltage in this circuit is V1. There are three connections to this node and consequently three currents to consider. The direction of the currents in calculations is chosen to be away from the node.
- Current through resistor R1: (V1 - VS) / R1
- Current through resistor R2: V1 / R2
- Current through current source IS: -IS
With Kirchhoff's current law, we get:
This equation can be solved in respect to V1:
Finally, the unknown voltage can be solved by substituting numerical values for the symbols. Any unknown currents are easy to calculate after all the voltages in the circuit are known.
The fact that and implies that current flows in the opposite direction through R1 reflects the fact that assuming that current flows out of a node just helps us write equations that capture the circuit topology in order to write logically consistent equations. They are in no way a guess at the final current direction.
Another Example
[edit | edit source]Given the Circuit below, find the voltages at all nodes.
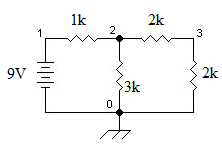
- node 0: (defined as ground node)
- node 1: (free node voltage)
- node 2:
- node 3:
which results in the following system of linear equations:
Therefore, the solution is:
Supernodes
[edit | edit source]
In this circuit, we initially have two unknown voltages, V1 and V2. The voltage at V3 is already known to be VB because the other terminal of the voltage source is at ground potential.
The current going through voltage source VA cannot be directly calculated. Therefore we can not write the current equations for either V1 or V2. However, we know that the same current leaving node V2 must enter node V1. Even though the nodes can not be individually solved, we know that the combined current of these two nodes is zero. This combining of the two nodes is called the supernode technique, and it requires one additional equation: V1 = V2 + VA.
The complete set of equations for this circuit is:
By substituting V1 to the first equation and solving in respect to V2, we get:

















