Circuit Theory/Analog Computer
Goal
[edit | edit source]Design an analog computer that generates a solution to this differential equation:
- f(t) is the input, the bump the car is going over
- v(t) is the output, the vertical motion of the car in response to the bump
- a2 is related to the spring constant of a shock absorber
- a1 is related to the damping coefficient and viscosity of the oil
- ao is varied depending upon the desired ride
- The goal is to vary a2, a1, and ao electronically, rather than build many models physically. This is modeling as done before WWII instead of using matlab or similar software.
- Modern applications of this include control systems (opening and closing valves in an industrial process, turning off and on motors, controlling a nuclear power plant).
Organizing
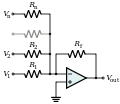
[edit | edit source]At first glance, need 6 op-amps, 2 for differentiation, 3 for scaling, 1 for adding.
But the adder can do scaling also.
Need to think about the overall circuit design too. The desired output is v(t). The function f(t) is an input. The derivatives are temporary values that are built from the output being feed back. So the math is going to look something like this:
Need to feed the output back into the input also ... and will take first derivative, then second, then feed into the adder with f(t). So the math would look more like this:
-
this takes the input and differentiates it so output is
-
this takes output of the first derivative which is negative and makes it positive again, so the second derivative will be negative also
-
this generates the second derivative which is now negative like the first derivative
-
this will take the negative and the negative (because was inverted) terms and adds them to a positive f(t), scaling appropriately to generate
Simulating
[edit | edit source] Assume the output of OA4 is v(t).
Assume the output of OA4 is v(t).
Then the output of OA1 is:
The output of OA2 is:
The output of OA3 is:
Assume V14 is f(t). Then the output of OA4, the adder is:
Comparing this to:
We can see that:
There are three knowns a0, a1, and a2, 10 unknowns and 3 equations. So the problem is under constrained, meaning that other requirements can be used to pick the resistor and capacitor values.