Circuit Theory/2Source Excitement/Node and Mesh
Jump to navigation
Jump to search

marked up for node analysis 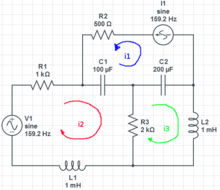
marked up for mesh analysis
The first step is to convert everything to phasors and impedances in symbolic form if possible:
Node Analysis
[edit | edit source]
Results using matlab:
Mesh Analysis
[edit | edit source]
Results using Matlab:
















