Circuit Idea/How do We Create Sinusoidal Oscillations?
Circuit idea: Connect two heterogeneous energy storing elements to each other and charge one of them with energy.

Questions to be answered
[edit | edit source]LC tank is a legendary electrical circuit, and conceiving sinusoidal oscillations in an LC tank is a popular electrical phenomenon. It is well described in physics, electricity and electronics resources (see for example one of the best LC explanations on the web[1]). Browsing through these resources you will probably get to know what an LC tank is and how it operates in terms of electricity. Only, although these resources explain in detail what an LC tank does they do not say how and why it does this magic.
The point is that LC oscillation is not only a specific electrical occurrence; this is a great worldly phenomenon. There are many its manifestations in "non-electrical" world (mechanics, pneumatics, hydraulics, etc.) If you want to penetrate deeply into its nature, you will begin asking dozens of "philosophical" questions that are still unanswered. What are these questions? Here are some of them.
Why does an LC tank consist of two "heterogeneous" accumulating elements (a capacitor and an inductor)? Why is it not assembled by two "homogeneous" elements (both capacitors or both inductors)? What is the role of these elements in the LC circuit? What do they actually do there? What are they? Why does the energy in an LC tank "have no peace"? What makes it circulate (in theory, infinitely) between the two components? What makes the accumulating elements discharge completely? Why does an LC oscillation have a sinusoidal shape? Why is it no with linear or other shape? Why does not the LC natural frequency depend on the amount of the "pushed" energy? Why is the oscillation curve symmetrical? What are the differences between LC and other (RC, relaxation, etc.) oscillations? Is there any likeness between them and what is it? What is the connection between the two-component LC tank and the one-component pendulum? What is the "capacitor" and what is the "inductor" in a pendulum?
In this story, we will answer these questions in a manner that is quite different from the classical one. Here, we will forget temporarily the conventional "electrical" LC explanations (e.g., "...the inductor discharges through the capacitor and the field collapses..."); they will help us not so much to answer the questions above. Because we, human beings, cannot understand concrete (electrical) phenomena by concrete (electrical) explanations. In order to grasp the specific electrical ideas, we need first to reveal the most general, non-electrical ideas behind the concrete electrical phenomena.
In this exciting story we, circuit ideators and circuit philosophers, will try by ourselves to find out the truth about this great worldly phenomenon. For this purpose, we will re-invent and build step-by-step the famous LC tank, in order to grasp the basic idea benind it. Thus we will create a general, non-electrical philosophy for the specific electrical LC phenomenon.
Creating the first half of the sinusoid
[edit | edit source]Initial steady quantity
[edit | edit source]General sources. First of all, to do something in this world, we need a steady power source. According to the two kinds of energy - kinetic and potential, there are also two kinds of sources - a flow-like source and a pressure-like one (see the top of Fig. 1a). A flow-like source keeps up a constant flow rate and a pressure-like source keeps up a constant pressure difference of something (air, water, oil, spring tension, etc.) - Fig. 1b.

Electrical sources. Similarly, in electricity we have two kinds of sources - a current source keeping up a constant current and a voltage source keeping up a constant voltage (see the bottom of Fig. 1a).
The problem. Only, for a variety of reasons, we want to make the output quantity of the steady source begin changing periodically through time. Of course, we can take a varying source and just begin controlling it; but we want it to oscillate by itself, without our help. So, the problem is:
The first quarter
[edit | edit source]Making a quantity depend on time
[edit | edit source]First and foremost, we have to make the steady quantity depend on (change through) time. At this point, it is not so important how it varies in time; it is only important that it changes in time. So, the main question is: How do we make time-dependent quantities?
Philosophy. Obviously, we have to start some process in time (but what is time?:) In order to make something change, we have to take from it or to give to it; this means to move something from one place to other... One source is not enough for this purpose since it keeps up steady its output quantity; we need two elements - source and load connected to each other, to begin transferring energy from the source to the load (and maybe, v.v.) We already have a source; it remains to choose the kind of load.
A need of accumulating. A resistor is useless for such a load since it can instantaneously change current (when voltage is instantaneously changed). A resistor cannot store energy, it cannot "remember". It is clear that we have to begin transferring and storing some quantity in an accumulating element (an integrator). Integrators can accumulate energy, matter or information; mostly they store energy. So, we can make its output quantity increase by continuously adding energy to the accumulator and to decrease it by continuously subtracting energy from the accumulator. According to the two kinds of energy - kinetic and potential, we can build two kinds of integrators - flow-to-pressure and pressure-to-flow integrator.
Flow-to-pressure integrator. In this case, we begin converting a flow-like quantity (carrying kinetic energy) into a pressure-like quantity (carrying potential energy) and storing it into an accumulating element having a property to contain (see the top of Fig. 2a). The energy moves from the flow to the pressure accumulator and the pressure-like quantity begins changing linearly through time (Fig. 2b).

Examples: moving mass pushes a spring, an accelerated pendulum raises, a child wind up a spring motor, an archer draws a bow, a flywheel puts in motion a toy car, a motor lifts a mass, an air pump blows up a tire, a water pump fills a reservoir, etc. We can even, in order to feel the process, imagine that very we are moving (in synectics, this technique for creative thinking is known as "empathy").
Note that the flow-to-pressure integrator consists of two heterogenous elements connected to each other - a source of kinetic energy and an accumulator of potential energy. If we connect two homogeneous elements to each other (a source of kinetic energy and an accumulator of kinetic energy), a big pressure appears and the process ceases momentarily; this arrangement will differentiate rather than integrate. A mechanical example: imagine what happens, if a moving car hits a car at rest.
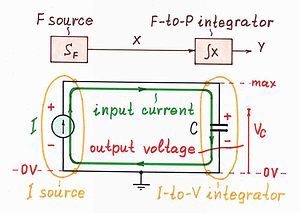
Current-to-voltage integrator. In electricity, we have two elements that can accumulate energy - the capacitor stores potential energy and the inductor stores kinetic energy. So, we can build two kinds of electrical integrators - current-to-voltage and voltage-to-current integrator. Let's begin with the first and more popular of them.
According to the general flow-to-pressure arrangement, in a current-to-voltage integrator we begin converting a current (carrying kinetic energy) into a voltage (carrying potential energy) and storing it into a capacitor. So, the circuit includes a current source charging a capacitor (see the bottom of Fig. 2a). As a result, the voltage across the capacitor changes linearly through time (Fig. 2b). Note the current enters the positive plate of the capacitor; so, the capacitor acts here as a load.
The circuit consists of two heterogenous electrical elements connected to each other - a current source and a capacitor. If we connect two homogeneous elements to each other (a current source and an inductor), a high voltage appears across them and the process ceases momentarily; the circuit will differentiate rather than integrate.
Rounding the curve...
[edit | edit source]So far, we have made the steady quantity change linearly through time. Thus, we have obtained a quantity that increases continuously in time. In many cases (e.g., in ramp generators), this is a desired feature; but here we need a sinusoidal shape, not a linear one. So, the new problem is, "How do we round the linear curve?"
Then, let's scrutinize the present linear curve trying to find a remedy for converting it to a sinusoidal shaped. What does it mean? It means that after the quantity was changing linearly for a while, at this point it has already to begin changing (decreasing) its slope, to bend down, "to loose its nerve" (Fig. 3b). How do we achieve such an effect?
The general idea. So far, we have obtained a linear change by an integrator that was integrating a constant quantity. Now, we ask ourselves, "How do we make the integrator to slow down its output quantity?" The answer is: "By decreasing the input quantity." Here is the basic idea needed - to decrease the input quantity.
...by reducing the effective voltage...
[edit | edit source]Remember the imperfect RC integrator, whose linear curve is naturally rounded (exponentially shaped).


The "problem" (here, this is an advantage) of this integrating circuit (Fig. 3a) was that the capacitor was been charging by an imperfect "self-made" current source (assembled by a voltage source V and a resistor R). As a result, the voltage drop VC across the load (the capacitor) enervates the excitation voltage V; in this way, it disturbs the imperfect current source. In this arrangement, the voltage difference VR = V - VC determines the current I instead the excitation voltage V. As the current-creating voltage VR decreases through time the current decreases as well. Because of this decreasing in time current source the curve of VC begins decreasing its slope as well; this is what we want here.
...by decreasing the input current...
[edit | edit source]But here we have a perfect current source whose current does not depend on the voltage across the load (the capacitor). That means, if the load voltage increases, our current source increases its internal excitation voltage as well thus eliminating the voltage disturbance.[2] It looks strange but here the problem is the very perfect current source:) What do we do then? How do we make it behave as an imperfect one?
Having been looking at Fig. 3, some rudiments of new idea can begin conceiving in our minds... It turns out that we can manage to round, change and finally decrease the slope of the curve by making in some way the perfect current source begin decreasing by itself the current produced when the voltage across the load increases... We can generalize this assertion:
Whereas in the imperfect RC integrator the rounding is a result of decreasing the effective current-creating voltage VR, here the rounding will be a result of decreasing the whole input voltage V. Well, it is wonderful but how can we do this magic?
Of course, we can regulate the input voltage but this will require some electronic circuit. Do not remember here we "invent" the simplest "thing" that can oscillate; so, we need the simplest "trick" that can exist! What is it?
...by exhausting the input current source
[edit | edit source]It seems another new idea begins conceiving... We would like to decrease a quantity... It is produced by a power source... It has a limited reserve of energy... Eureka! If we begin taking away energy from the source, its output quantity will begin decreasing! Here are some examples: pushing the spring, the moving mass begins slowing its speed; running into an elastic barrier, we slow your run; rising, the pendulum begins slowing, etc.


The right idea. If, in a kind of way, the input current source begins weakening, depleting, exhausting its reserve of energy, the source's current will begin decreasing as well (Fig. 4a). As a result, the voltage across the capacitor will begin changing slowly and its curve will begin "loosing its nerve" (Fig. 4b). Is this source an imperfect current source as above? No, it is not; it is an exhausting but still a perfect constant current source that decreases gradually its output quantity. Here, the current decreases not because of the load voltage (as it was at the imperfect RC integrator) but because of the load consumption!
What electrical element can serve as such an exhausting perfect current source? Of course, an inductor charged with kinetic energy! It seems strange but it produces a "constant" current (for quick load changes) that gradually decreases:
Eurika! We have obtained the arrangement needed (Fig. 4a); we have almost "invented" the LC tank:
Note the current leaves the positive lead of the inductor; so, the inductor acts here as a source.
Stopping the "movement"
[edit | edit source]We are already at the top of the curve and now it's time to stop here. But how can we make the integrator's output quantity stop? Will it stop, if we stop the input quantity? No, it will not. Even if we decrease significantly the input quantity, the integrator will not cease changing its output quantity. The only way to stop the integrator's output quantity is to zero the input quantity. To convince yourself of this phenomenon imagine you fill a vessel with water: even if you lower the rate of flow to an insignificant quantity, the water level will still continue increasing. More examples: if you feed up gradually a money deposit with small change, the amount of money increases slowly (but still increases) through time; pushing the spring, the moving mass finally stops; moving pendulum stops at the top.


The "exhausting" flow source above that produces gradually decreasing flow has already helped us to change the slope of the curve and to round it. Here, at the top of the curve, it can help us now to stop the "movement". Indeed, at the maximum of the quantity, the source has completely exhausted its reserve of kinetic energy. Actually, at this instant, it is not merely a source; it is an empty source. As a result, the flow becomes zero (Fig. 5a) and the integrator stops changing its output quantity (Fig. 5b). Then, let's draw another conclusion:
In the electrical implementation (an LC tank) the inductor serves as an exhausting current source (Fig. 5a). At the top of the curve, it has fully discharged and produces no current. As a result, the voltage across the capacitor stops changing.
Why does the inductor discharge completely? We have already said that an inductor is an exhausting but still a perfect constant current source. Furthermore, an inductor is a natural, pure, monolithic current source; it is not an artificial current source that is composed of an internal voltage source and a resistor as in the case of the imperfect RC integrator. This means it can create a high enough voltage across the load to produce the current desired. In other words, the current created by the inductor does not depend on the voltage across the capacitor; this voltage is not an "opposition" to the current. As there is nothing to oppose the current produced by the inductor, no matter how small energy is left in the inductor; the current continues flowing until the inductor discharges completely.
The opposite arrangement. In order to feel the difference, compare this "discharging inductor -> charging capacitor" arrangement with the "discharging capacitor -> charging inductor" arrangement mentioned below. In the latter case, the charged capacitor is discharging and the empty inductor is charging. In this way, both the elements are finally charged with some energy. The voltage across them has some middle value - the point of the system equilibrium.
The second quarter
[edit | edit source]Reversing the direction
[edit | edit source]So far, we have been "moving" in one direction (initially fast, then slow) and finally we have stopped at the top of the curve. As we have been continuously "pushing" energy into the accumulator (the integrator) its output quantity has been continuously increasing in magnitude. Thus we have obtained a monotonous and quite uninteresting signal:) However, we would like to obtain a periodical quantity; so, we have here, at the top of the curve, to change, to reverse in some way the direction of the "movement". Something has to happen at this point to make the integrator's output quantity begin decreasing... What can cause this to happen?
Looking at many analogies of integrating, we can conclude that the only way to change the direction of the integrator's (here, a pressure-like) output quantity is to change the direction, not the magnitude, of its input (here, a flow-like) quantity. Imagine again the water analogy: while we fill the vessel the water level increases; to make it decrease, we have to begin emptying the vessel. Or imagine the money analogy: while you feed up gradually the deposit, the amount of money increases through time; to make it decrease, you begin "emptying" the deposit. Of course, we should mention again the famous mechanical analogy: after the moving mass stops, the spring begins beating it back; after we strike into the elastic barrier, it repulses us, it acts as a kind of "reverser" that changes the direction of our movement. We are ready enough to draw two conclusions:
But this integrator is not only a bare accumulator... Remember that so far a flow-like source has been exhausting slowly and charging this pressure accumulator (a flow-to-pressure integrator). So, at the end of this process, the integrator has transmuted into an opposite pressure source. Now, it is a charged with energy accumulator; it has become a power source! So, it can by itself change its output quantity by passing a current through the load. But what is the load here? The other element (the former source) acts now as a load. What kind of load is it? Remember it is an accumulutaing element that stores kinetic energy.
Pressure-to-flow integrator. So, we begin now converting a pressure-like quantity (carrying potential energy) into a flow-like quantity (carrying kinetic energy) and storing it into an accumulating element having a property of inertness (see the top of Fig. 6a). Now, the energy moves in an opposite direction - from the pressure to the flow accumulator, and the flow-like quantity should change linearly through time (Fig. 6b).


Examples: a spring (or gravitation) puts in motion a mass, a spring motor actuates a toy, a child accelerate a flywheel car, air compressed in a reservoir spins an air turbine, water stored in a lake spins a water turbine, a boulder rolls down a mountain going faster and faster, "putting the pedal to the metal" makes a constant-horsepower engine push a car faster and faster, pressurized air escaping from a balloon rocket causes it to accelerate and fly away, water rocket, "pushing off" with your foot starts a bicycle moving, etc.
Note that this arrangement includes again two heterogenous elements connected to each other - a source of potential energy and an accumulator of kinetic energy. If we connect two homogeneous elements to each other (now, a source of potential energy and an accumulator of potential energy), a big current flows and the process ceases momentarily. As above, this arrangement will differentiate rather than integrate.
Voltage-to-current integrator. According to the general pressure-to-flow arrangement, in a voltage-to-current integrator we begin converting a voltage (carrying potential energy) into a current (carrying kinetic energy) and storing it into an inductor. So, the circuit includes a voltage source charging an inductor (see the bottom of Fig. 6a). As a result, the current through the inductor should change linearly through time (Fig. 6b). Note the current leaves the positive plate of the capacitor (so, it acts here as a source) and the current enters the positive plate of the inductor (so, it acts here as a load).
The circuit consists of two heterogenous elements connected to each other - a voltage source and an inductor. If we connect two homogeneous elements to each other (a voltage source and a capacitor), a big current flows through them and the process ceases momentarily; the circuit will differentiate rather than integrate.
An exhausting voltage source As above, in order to round the curve, our source has to have a limited reserve of energy; it has to exhaust, deplete gradually. The capacitor serves exactly as such an exhausting voltage source. Only, whereas before we wanted to round the curve in the final part, here we want to round it in the initial part. Let's see what the situation is. In the beginning, the current is low and the inductor consumes a little energy. Later, the current through the inductor increases and it begins consuming more and more energy from the voltage "source". Wonderful! The curve is rounded in its initial part exactly as we wanted!
Crossing the zero level
[edit | edit source]At the end of this stage, the source has completely exhausted its reserve of potential energy. As above, at this instant, it is not a source; it is just an empty source. As a result, the pressure becomes zero (see the top of Fig. 7a) and the pressure-to-flow integrator stops increasing its output quantity (Fig. 7b). It has accumulated maximum kinetic energy at this point.
If you look again at our favorite analogies, you will see that the moving masses from all the mechanical examples above are maximum accelerated (e.g., imagine how fast we run at this point:) Here, we have to remember that these objects have an interesting property - inertness. If they were non-inert, they would stop at this point and the system would be in state of equilibrium. But they are inert; that's why, they pass by this zero point (a neutral position) and continue moving... As if there are some devilish force:) that make them continue moving beyond this point (remember Newton's laws of motion).


We can already compare the behavior of the two different accumulating elements. We have already seen how the accumulator of potential energy (the capacitor) acts as a kind of an elastic barrier that repulses the moving "mass" thus reversing the direction of the movement. Now, we can see how the accumulator of kinetic energy (the inductor), because of its inherent inertness, "passes" beyond the equilibrium point (the zero level) and continues "moving".
A little while ago, the capacitor served as an exhausting voltage source. At this point, it has fully discharged and there is no voltage across it. The current through the inductor has its maximum rate but it has stopped changing. So, at the end of the stage both the current and the energy consumption have increased to its maximum value.
The opposite arrangement. We have already managed to answer why the inductor discharges completely through the capacitor - because it is a natural true current source. Now situation is even more interesting. In order to answer why the capacitor discharges completely, let's again consider the opposite arrangement - a charged capacitor connected to an empty one. If you prefer analogies, imagine communicating vessels where the one vessel is full and the other is empty. We know the result: a big current flows in the beginning; the "opposing" voltage across the initially empty capacitor (the water level of the initially empty vessel) begins rising rapidly; as a result, it decreases and finally stops the current. At this point, the energy is distributed between the two capacitors and the system is at static equilibrium (remember Newton's third law). The initially charged capacitor has not managed to discharge completely.
Why does the capacitor discharge completely? Contrary, if we connect the charged capacitor to an initially empty inductor (the present case), the current is negligible in the beginning and the capacitor begins discharging slowly through the inductor. In the course of time, the inductor lets the current increase gradually. The increasing current discharges the capacitor more and more thus hastening its discharging; finally, the capacitor is fully discharged. Figuratively speaking, an inductor has a time-dependent behavior: in the beginning, it consumes little current but in the end it devours a large quantity of current (a capacitor has an opposite time-dependent behavior - in the beginning, it devours a maximum current but in the end it consumes little current).
At first glance, it seems the system is moving to its equilibrium; we might suppose it has managed to reach this point and the energy inhabiting the LC tank "has found a peace"...
Creating the second half of the sinusoid
[edit | edit source]So far, we was considering in details how to create the first half (the first and the second quarter) of the sinusoid curve. The common sense suggests that we can create in the same manner the second half. Then, let's try it.
The third quarter
[edit | edit source]

At the end of the second quarter and at the beginning of the third quarter, the situation is the same as it was at the first quarter. From one side, the inductor is fully charged with kinetic energy and it has transmuted from an integrator into a current source again (Fig. 8a). From the other side, the empty capacitor is connected to this "current source". What does the inductor begin doing then? Of course, it will start charging the capacitor and begin exhausting gradually. The only difference is the direction of the current that creates across the capacitor a negative voltage. As a result, the curve begins falling (in the beginning - rapidly, then - slowly) and finally stops at the bottom. It is rounded in the final part as we want.
The fourth quarter
[edit | edit source]

Similarly, in the beginning of the final fourth quarter, the situation is the same as it was at the second quarter. From one side, the capacitor is fully charged with potential energy and it has transmuted from an integrator into a voltage source again (Fig. 9a). From the other side, the empty inductor is connected to this "voltage source". What does the capacitor begin doing then? Of course, it will start charging the inductor and begin exhausting gradually. The only difference is the negative voltage across the capacitor that creates a current with an opposite direction. As a result, the curve stays under the zero level but begins rising (in the beginning - slowly, then - rapidly) and finally crosses the zero level (Fig. 9b). It is rounded at the initial part as we want.
A generalization
[edit | edit source]At the end of this incredible story, let's generalize what we have managed to do.
Basic structure
[edit | edit source]
In the beginning, we have assembled a system of two connected to each other heterogeneous elements that can process two different kinds of energy: they can convert energy (acting as true energy converters), store energy (acting as accumulators) and supply loads by energy (acting as sources). The one of them can convert potential to kinetic energy, store the kinetic energy and transfer gradually this kinetic energy to the load keeping up a gradually decreasing flow-like quantity; the other element can convert kinetic to potential energy, store this potential energy and transfer gradually this potential energy to the load keeping up a gradually decreasing pressure-like quantity. The first element has a property of inertness while the second one has a property of strain; so, the first element can "pass" beyond the equilibrium point and continue moving while the second one can reverse the direction of the "movement". Each of these reversible elements can act as a load as well as an gradually exhausting source. These kinds of rechargeable sources are fitted perfectly to each other - when the one element acts as a flow-output source, the other one acts as a flow-input load and v.v. - when the other element acts as a pressure-output source, the first one acts as a pressure-input load. As a result, they can exchange energy gradually in time between each other.
Electrical circuit
[edit | edit source]In electricity, we have implemented this arrangement by connecting an inductor and a capacitor to each other; thus we have obtained the famous circuit of an LC tank. The inductor can convert voltage to current, store the kinetic energy of moving electrons in the magnetic field and transfer gradually this kinetic energy to the load keeping up a gradually decreasing current; the capacitor can convert current to voltage, store this potential energy in the electrostatic field and transfer gradually this potential energy to the load keeping up a gradually decreasing voltage. Simply speaking, the inductor acts as a rechargable current source and the capacitor acts as a rechargable voltage source.
Operation
[edit | edit source]In the beginning (see point a on Fig. 11), there is no energy in the LC tank; it is at rest. Then, we charge the inductor connecting momentarily a current source (with the same success we might charge initially the capacitor connecting momentarily a voltage source and this is the more usual case in electronic oscillators). After we disconnect the source a wonder begins...

Phase 1. The inductor (acting as a positive current source) discharges gradually through the capacitor (acting as an accumulating load). The energy moves from left to right; the voltage increases above the zero level. At the top (point b), the capacitor becomes a positive voltage source.
Phase 2. The capacitor (acting as a positive voltage source) discharges gradually through the inductor (acting as an accumulating load). The energy moves from right to left; the voltage decreases toward the zero level. At the end (point c), the inductor becomes a negative current source.
Phase 3. The inductor (acting as a negative current source) discharges gradually through the capacitor (acting as an accumulating load). The energy moves from left to right; the voltage decreases below the zero level. At the bottom (point d), the capacitor becomes a negative voltage source.
Phase 4. The capacitor (acting as a negative voltage source) discharges gradually through the inductor (acting as an accumulating load). The energy moves from right to left; the voltage increases toward the zero level. At the end (point e), the inductor becomes a positive current source.
Assembling. If there are no losses in the circuit, the four phases will repeat continuosly one after another (1 - 2 - 3 - 4 - 1 - etc.) thus forming the whole LC sinusoidal oscillation (Fig. 11). The LC tank keeps the initially injected energy intact but this energy is not at rest, it "has no peace". The energy inhabitting the LC tank moves continuously to and fro between the two elements and changes alternatively from one to other form. Accordingly, the electrical quantities (current and voltage) representing the corresponding kinds of energy (kinetic and potential) change in а sinusoidal manner; so, we can use them as outputs.
Natural frequency
[edit | edit source]Energy independence. As we have seen, after we inject energy into an LC tank it begins producing a sinusoidal oscillation with a natural period. If we inject more energy, the amplitudes of the voltage and the current increase but they change more quickly and v.v.; as a result, the natural period remains constant. The reason of this "energy-independent time behavior" is the variable consumption: when we increase the initially injected energy, the consumption increases as well and v.v. In the case when we charge the inductor with more energy, the current passing through the inductor will reach a bigger magnitude and then, when we disconnect the "pushing" current source, this bigger current will determine a bigger consumption; as a result, the time remains the same. In the other case, when we charge the capacitor with more energy and then disconnect the "pushing" voltage source, the inductor will begin gradually consuming a bigger current; as a result, again the time remains the same (we can observe a similar "time constant" effect in an RC circuit). So, we can make a conclusion: the natural frequency of an LC oscillation does not depend on the amount of the "pushed" energy (on the magnitudes of the voltage and current).
LC dependence. Contrary, if we change the values of the "storage properties" (inductance L and capacity C) of the accumulating elements (inductor and capacitor), the natural frequency changes as well. We can easily realize by intuition that the bigger the value of the storage property is, the bigger the duration of the corresponding quarter period is (e.g., if the capacitor is "bigger", the inductor needs more time to charge it).
Symmetry. But why the oscillation remains symmetrical (TPhase1 = TPhase2 = TPhase3 = TPhase4), even if we change the value only of one storage property (the inductance L or the capacity C)? The answer is simple. During an every half of a period, each of the two elements changes two times its "role": during the first quarter it acts as a load and during the second quarter it acts as a source. In this way, its storage property defines the duration of both the neighboring quarters; changing the property, we change simultaneously both the quarter durations. As a result, the curve remains symmetrical when we change either the inductance L or the capacity C or both of them.
Final conclusion
[edit | edit source]LC tank is the simplest electrical circuit that can generate oscillations with a perfect sinusoidal shape. This unique circuit consists only of two elements but it can do all that is needed to produce sinusoidal oscillations somewhat by itself. It is an almost ideal circuit that resemble a perpetual motion machine:) - we have only to inject initial energy and then it continues acting by itself.
See also
[edit | edit source]Oscillation is a general Wikipedia article about oscillations in nature.
References
[edit | edit source]- ↑ An electric pendulum by Tony Kuphaldt is a classical but maybe the best written story about the operation of LC tank, although it seems to imply that pendulums exhibit Simple Harmonic Motion (they don't, quite).
- ↑ Keeping a constant current by a following excitation voltage reveals the philosophy of constant current sources.
External links
[edit | edit source]- Introduction to oscillators and
- LC oscillators present very well the classical "electrical" viewpoint at LC tank operation.
- How the parallel-LC circuit stores energy is another excellent LC resource.
- A lecture on LC circuit is a series of slides containing useful formulas.
- LC tank is an interesting and well illustrated story about LC tank.
- The physics of resonance is a classical but very well written story about the LC tank operation.
- How Tesla coils work has a concise but very informative introduction about LC tank.
- LC circuits makes a comparison between the electrical and mechanical implementation.
- Inductors - an excellent material about inductor's behavior.