CLEP College Algebra/Functions
In math, it is often important to describe how a certain set of input from some certain operation can at some point represent the output of such operations. The tool math has created for this regard is called the function. The formal definition of a function can perhaps be a very tricky obstacle to grasp fully, and the best way to understand it is to perhaps use the intuitive concepts in practicum (as a preliminary step towards the goal, understanding). Therefore, we will begin this chapter by giving an intuition behind the processing.
The Intuitive Uses and Definition of Functions
[edit | edit source]You can think of a function as a kind of machine. You feed the machine raw materials (as an input), and the machine changes the raw materials into a finished product (the output). Let us describe a cook as a function. Handing a piece of lettuce to the cook would result in chopped lettuces as the output. The output is minced lettuces. A function in mathematics is somewhat equivalent. This viewpoint can get us far enough to at least understand its real-life applications.
|
Example 1.1(a): A function in everyday life 1 Think about dropping a ball from a bridge. At each moment in time, the ball has a velocity, . The velocity of the ball is a function of time. This type of function is called real-valued since the "finished product" is a number (or, more specifically, a real number). |
|
Example 1.1(b): A function in everyday life 2 Imagine the mean temperature of a river deviates everyday by . If the temperature of the river is sampled everyday, with samples per day, and the population mean of all the samples collected is while the deviation , then one way we can reflect the distribution of the temperature of the river is by using the Normal (or "Gaussian") function, which is written here below: If instead, the river only ever deviates from the mean, then one could write it in terms of absolute values: Either way, a function is used in everyday life. |
Think of a real-valued function as an input-output machine; you give the function an input, and it gives you an output which is a number (more specifically, a real number). For example, the squaring function takes the input and gives the output value . The same squaring function takes the input and gives the output value .
There are many ways which people describe functions. In the first example, a verbal descriptions is given (the height of the ball above the earth as a function of time). In the second example, some different operations of certain functions are given. The specifics of using operations to describe functions are given below:
- A function is given a name (such as ) and a formula for the function is also given. For example, describes a function. We refer to the input as the argument of the function (or the independent variable), and to the output as the value of the function at the given argument. (Note: more on this notation is described in the next section.)
- A function is described using an equation and two variables. One variable is for the input of the function and one is for the output of the function. The variable for the input is called the independent variable. The variable for the output is called the dependent variable. For example, describes a function. The dependent variable appears by itself on the left hand side of equal sign.
When a function is given a name (like in number 1 above), the name of the function is usually a single letter of the alphabet (such as or ). Some functions have names that are multiple letters (like the sine function .
Let us practice assigning a function using the second method described above by revisiting the first example again:
|
Example 1.1(c): The Ball's Velocity as a Function of Height Imagine, as a physicist, you were asked to describe the velocity as a function of height. Here is what may be best described (using energy equations):
The above information allows us to approximate the ball's velocity as a function of height:
|
The above equation is an example of a special type of function called a composite function. This function will be explained in much more detail later. For now, an intuition is all that is needed.
Hopefully, an intuition has begun forming inside the mind of the student. Let us see how to evaluate functions at certain inputs now.
|
Example 1.1(d): Inputs Given an Output. What is it? (Part 1) If we write , then we know that
Based on the above bullet points, the way to evaluate a function at a certain point is Therefore, the value of is
|
|
Example 1.1(e): Inputs Given an Output. What is it? (Part 2) Let us return to the function we derived in Example 1.1(c). With the function , where , we know the following is true:
When working with functions that is founded in real-life applications, it is important to also keep in mind units. Since SI units are used, and the gravitation constant is in meters per second-squared, the height will be in meters. We want to know what the velocity is if the ball is halfway between the bridge and the ground, . Assume . Let us begin evaluating the function: Therefore, the value of is
|
A Note on Notation
[edit | edit source]Functions are used so much that there is a special notation for them. The notation is somewhat ambiguous, so familiarity with it is important in order to understand the intention of an equation or formula.
Though there are no strict rules for naming a function, it is standard practice to use the letters , , and to denote functions, and the variable to denote an independent variable. is used for both dependent and independent variables.
When discussing or working with a function , it's important to know not only the function, but also its independent variable . Thus, when referring to a function , you usually do not write , but instead . The function is now referred to as " of ". The name of the function is adjacent to the independent variable (in parentheses). This is useful for indicating the value of the function at a particular value of the independent variable. For instance, if
- ,
and if we want to use the value of for when is equal to , then we would substitute for on both sides of the definition above and write
This notation is more informative than leaving off the independent variable and writing simply , but can be ambiguous since the parentheses next to can be misinterpreted as multiplication, . To make sure no person is confused by notation accidentally, follow this procedure:
- Define the function by equating it to some expression.
- Give a sentence like the following: "At , the function is..."
- Evaluate the function.
This procedure can change if the student is doing a multiple choice exam since communication is not important in that context.
Formalizing the Intuition
[edit | edit source]As of now, the definition below should not make too much sense. Read the definition so that you may see where the we gain the understanding of the mapping.
a mapping associating the elements of one set called the domain, , with the elements of another set called the range, , is a function. For each value we select from the domain of the function, there exists exactly one corresponding element in the range of the function.
For now, analyze the definition. Take notice at the implication of an element in the range being found through the correspondence of the element mapping from the domain. An example of how is given below.
|
Let function for all . For what value of gives ? In mathematics, it is important to notice any repetition. If something seems to repeat, keep a note of that in the back of your mind somewhere. Here, notice that and . Because is equal to two different things, it must be the case that the other side of the equal sign to is equal to the other. This property is known as the transitive property (always remember the Properties of Real Numbers): Next, simplify — make your life easier rather than harder. In this instance, since has as a like-term, and the two terms are fractions added to the other, put it over a common denominator and simplify. Similar, since is a mixed fraction, . Multiply both sides by the reciprocal of the coefficient of , from both sides by multiplying by it.
The value of that makes is .. |
Classically, the element "picked" from the domain is pictured as something that is fed into the function (the input) and the corresponding element in the range is pictured as the output. Notice the specificity of the language herein: an input is selected from the domain, meaning the domain is the set of all inputs; an output results from that specific input, meaning the range is the set of all possible outputs.
Since we "pick" the element in the domain whose corresponding element in the range we want to find, we have control over what element we pick and hence this element is also known as the "independent variable". The element in the range is beyond our control and is "mapped to" by the function. This element is hence also known as the "dependent variable", for it depends on which independent variable we pick. Since it is an element, the input is also known as the independent variable. Similar, the output is also known as the dependent variable.
The intuition of functions is better to grasp at first (for most students). However, the importance by which the formal definition of functions are to the foundations of algebra as we know it means that the formal definition should be viewed in high regards. Nevertheless, this does not mean that an intuition is unnecessary or even detrimental. Rather, students should be able to understand both viewpoints, and be able to relate them. As such, we argue that students should hold on to both viewpoints.
To recap, a function is a mapping of some element , called the domain, to exactly one element , called the range, such that . The image below should help explain the modern definition of a function:
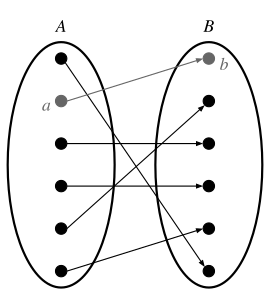
The Foundations of Functions: The Mapping, the Cartesian Cross Product, and Ordered Pairs
[edit | edit source]Now that we understand the set, we will begin understanding the fundamental property of the function (the mapping). However, how do elements "map" to another set? It would be when the combination is "tied" to another element. Defining "tied" would be tricky without the help of sets. However, the set nicely defines tying, and it is through ordered pairs.
An order pair is defined to be a set written in the form of as:
- .
The logic in this is that the sets contained within are an element that is dependent on the order of the written pairs. Because uses both elements, the set gives the second coordinate based on the order of written pairs. However, this definition does not hold for , since it evaluates to give , which does not give an accurate reading of the second coordinate. However, this definition is good enough for the purposes of this textbook. Plus, the knowledge described herein is typically not taught in a College Algebra course.
Let and be two distinct sets. If we were to combine these two sets, it would be defined as the cartesian cross product (read aloud as cross ). is the set of ordered pairs whereby and :
- (read aloud as cross is the set that contains the ordered pair such that is in and is in . The wedge, is the logical symbol for "and").
The nature of the Cartesian Cross Product is hopefully self-evident. When two sets are combined as such, the ordered pair results. This is very close to the definition of the function. After all, the subset of this product is the function (for the most part).
Let and be two distinct sets. A mapping from to is a relation such that a subset of the cross product results in under the following conditions:
- For all and for all ,
- The ordered pairs and both in the subset
- Imply , and
- For all , there exists a such that .
The notation or is a condensed formatting of the definition (read aloud as maps into ).
All the above definition is saying is that given the cartesian cross product of the sets, called the domain and range, there exists a relation of the ordered pair that relates the domain to the range. For this book, the first notation () is preferred.
Finding New Properties of Functions Using Sets
[edit | edit source]From the definitions above, new questions now arise. Here are the three main ones: can a function be (1) one-to-one? (2) many-to-one? (3) one-to-many? Consider each case.
- A function is considered one-to-one if an element from domain of function , leads to exactly one element from range of the function. By definition, since only one element is mapped by function from some element , implies that there exists only one element from the mapping. Therefore, there exists a one-to-one function because it complies with the definition of a function. This definition is similar to Figure 1.
- A function is considered many-to-one if some elements from domain of function maps to exactly one element from range of the function. Since some elements must map onto exactly one element , must be compliant with the definition of a function. Therefore, there exists a many-to-one function.
- A function is considered one-to-many if exactly one element from domain of function maps to some elements from range of the function. If some element maps onto many distinct elements , then is non-functional since there exists many distinct elements . Given many-to-one is non-compliant to the definition of a function, there exists no function that is one-to-many.
The modern definition describes a function sufficiently such that it helps us determine whether some new type of "function" is indeed one. Now that each case is defined above, you can now prove whether functions are one of these function cases. Here is an example problem:
|
Given: , where and are constant and . Prove: function is one-to-one. Notice that the only changing element in the function is . To prove a function is one-to-one by applying the definition may be impossible because although two random elements of domain set may not be many-to-one, there may be some elements that may make the function many-to-one. To account for this possibility, we must prove that it is impossible to have some result like that.
Assume there exists two distinct elements and that will result in . This would make the function many-to-one. In consequence, Subtract from both sides of the equation. Factor from both terms to the left of the equation. Multiply to both sides of the equation. Add to both sides of the equation. |
There are a few more important ideas to learn from the modern definition of the function, and it comes from knowing the difference between domain, range, and codomain. We already discussed some of these, yet knowing about sets adds a new definition for each of the following ideas. Therefore, let us discuss these based on these new ideas. The below definitions are a little confusing. The best way to interpret these is to draw an image. To the right of these definitions is the image that corresponds to it (including a formal definition of the corresponding definitions).

- The domain is defined to be a set with all elements mapping to at least one unique .
- The set of elements in and implies is the range of the function in the cartesian cross product, whereby the set of all elements maps to at least one unique element . That is, the range is the set of all elements that was mapped by some to one corresponding .
- The codomain is the set , where it is not necessarily the case that all elements was mapped by some . That is, the set of all elements found in is the codomain.
The abstract concepts can also be made less confusing by using a function that can put these concepts into more concrete terms. Assume there is a function whereby . Let this function be where . Let us write down what the domain, range, and codomain is for this particular function:
- Domain: or or simply . In this instance, the domain is the set of all elements of except , since this one cannot be mapped to some element in .
- Range: or or simply . In this instance, the range is the set of all elements of except , since this one cannot be mapped by some element in .
- Codomain: or or . This includes the one element that we were not allowed to map.
There is one more final aspect that needs to be defined. We already have a good idea of what makes a mapping a function (e.g. it cannot be one-to-many). However, three more definitions that you will often hear will be necessary to talk about: injective, surjective, bijective.

- A function is injective if it is one-to-one. That is, for and , if , then . Otherwise, it cannot be one-to-one. The same definition from before applies for one-to-one (realize that the definition of injective and one-to-one are the same).
- A function is surjective if it is "onto." That is, the mapping has as the range of the function, where the codomain and the range of the function are the same.
- A function is bijective if it is both surjective and injective.
Again, the above definitions are often very confusing. Again, another image is provided to the right of the bullet points. Along with that, another example is also provided. Let us analyze the function .
|
Given: , where is constant and . Prove: function is non-surjective and non-injective. Notice that the only changing element in the function is . Let us check to see the conditions of this function.
Is it injective? Let , and solve for . First, divide by . Then take the square root of . By definition, , so Notice, however, what we learned from the above manipulation. As a result of solving for , we found that there are two inputs, , that give the same output,. This means that for some individual that gives , there are two different inputs that result in the same value. Because when , this is by definition non-injective. Is it surjective? As a natural consequence of what we learned about inputs, let us determine the range of the function. After all, the only way to determine if something is surjective is to see if the range applies to all real numbers. A good way to determine this is by finding a pattern involving our domains. Let us say we input a negative number for the domain: . This seemingly trivial exercise tells us that negative numbers give us non-negative numbers for our range. This is huge information! For , the function always results for our range. For the set , we have elements in that set that have no mappings from the set . As such, is the codomain of set . Therefore, this function is non-surjective! |
Functions are an important foundation of mathematics. This modern interpretation is a result of the hard work of the mathematicians of history. It was not until recently that the definition of the relation was introduced by René Descartes in Geometry (1637). Nearly a century later, the standard notation () was first introduced by Leonhard Euler in Introductio in Analysin Infinitorum and Institutiones Calculi Differentialis. The term function was also an innovation during Euler's time as well, being introduced Gottfried Wilhelm Leibniz in a 1673 letter "to describe a quantity related to points of a curve, such as a coordinate or curve's slope." Finally, the modern definition of the function being the relation among sets was first introduced in 1908 by Godfrey Harold Hardy where there is a relation between two variables and such that "to some values of at any rate correspond values of ." For the person that wants to learn more about the history of the function, this page has been provided for you.
Summary of the Set Definitions of Functions
[edit | edit source]This section is perhaps the hardest to understand. A summary is provided before the end of the chapter to help students further their understanding.
- A cartesian cross product is the operation , where and are two distinct sets.
- A mapping is a relation denoted by , where and are two distinct sets, such that the cartesian cross product results in the ordered pair for any given to some unique .
- A function is a mapping of the set of all inputs, the domain, , to the set of all corresponding outputs, the range, such that for any , the cross product is true for one and only one .
- The element is an input. The entire set is the domain (since it comprises all inputs). For any but and gives . implies is the range if the cartesian cross product results in . The set is the codomain.
- Let . A function is injective when for all and , if , then . Symbolically, .
- A function is surjective if the mapping has as the range and codomain of the function. Put another way, if , then is said to be surjective if .
- A function is bijective if it is both injective and surjective.
The summary only uses jargon terms. For the student that was able to understand and translate the jargon, they are ready to move on to the "Check your understanding." It is in the student's best interest to understand this section because the terms will come back again so that students may fully appreciate the intuition behind composite functions and inverse functions, which we will define in due time. Plus, these definitions are sometimes necessary for proofs. Having a good understanding of these basic foundations of functions will be helpful for the student throughout math, even for students who are not math majors.
Remarks
[edit | edit source]The following arise as a direct consequence of the definition of functions:
- By definition, for each "input" a function returns only one "output", corresponding to that input. While the same output may correspond to more than one input, one input cannot correspond to more than one output. This is expressed graphically as the vertical line test: a line drawn parallel to the axis of the dependent variable (normally vertical) will intersect the graph of a function only once. However, a line drawn parallel to the axis of the independent variable (normally horizontal) may intersect the graph of a function as many times as it likes. Equivalently, this has an algebraic (or formula-based) interpretation. We can always say if , then , but if we only know that then we can't be sure that .
- Each function has a set of values, the function's domain, which it can accept as input. Perhaps this set is all positive real numbers; perhaps it is the set {pork, mutton, beef}. This set must be implicitly/explicitly defined in the definition of the function. You cannot feed the function an element that isn't in the domain, as the function is not defined for that input element.
- Each function has a set of values, the function's range, which it can output. This may be the set of real numbers. It may be the set of positive integers or even the set {0,1}. This set, too, must be implicitly/explicitly defined in the definition of the function.

The vertical line test
[edit | edit source]The vertical line test, mentioned in the preceding paragraph, is a systematic test to find out if an equation involving and can serve as a function (with the independent variable and the dependent variable). Simply graph the equation and draw a vertical line through each point of the -axis. If any vertical line ever touches the graph at more than one point, then the equation is not a function; if the line always touches at most one point of the graph, then the equation is a function.
(There are a lot of useful curves, like circles, that aren't functions (see picture). Some people call these graphs with multiple intercepts, like our circle, "multi-valued functions"; they would refer to our "functions" as "single-valued functions".)





















































































































































