C++ Programming
Operators
[edit | edit source]Now that we have covered the variables and data types it becomes possible to introduce operators. Operators are special symbols that are used to represent and direct simple computations. They have significant importance in programming since they serve to define actions and simple interactions with data in a direct, non-abstract way.
Since computers are mathematical devices, compilers and interpreters require a full syntactic theory of all operations in order to correctly parse formulas involving combinations of symbols. In particular, they depend on operator precedence rules just as mathematical writing depends on order of operations. Conventionally, the computing usage of operator also goes beyond the mathematical usage (for functions).
C++, like all programming languages, uses a set of operators. They are subdivided into several groups:
- arithmetic operators (like addition and multiplication).
- boolean operators.
- string operators (used to manipulate strings of text).
- pointer operators.
- named operators (operators such as
sizeof, new, and delete defined by alphanumeric names rather than a punctuation character).
Most of the operators in C++ do exactly what you would expect them to do because most are common mathematical symbols. For example, the operator for adding two integers is +. C++ does allows the re-definition of some operators (operator overloading) on more complex types. This will be covered later on.
Expressions can contain both variables names and integer values. In each case the name of the variable is replaced with its value before the computation is performed.
Order of operations
[edit | edit source]When more than one operator appears in an expression, the order of evaluation depends on the rules of precedence. A complete explanation of precedence can get complicated, but just to get you started:
Multiplication and division happen before addition and subtraction. So 2*3-1 yields 5, not 4, and 2/3-1 yields -1, not 1 (remember that in integer division 2/3 is 0). If the operators have the same precedence they are evaluated from left to right. So in the expression minute*100/60, the multiplication happens first, yielding 5900/60, which in turn yields 98. If the operations had gone from right to left, the result would be 59*1 which is 59, which is wrong.
Any time you want to override the rules of precedence (or you are not sure what they are) you can use parentheses. Expressions in parentheses are evaluated first, so 2 * (3-1) is 4. You can also use parentheses to make an expression easier to read, as in (minute * 100) / 60, even though it doesn't change the result.
Precedence (Composition)
[edit | edit source]At this point we have looked at some of the elements of a programming language like variables, expressions, and statements in isolation, without talking about how to combine them.
One of the most useful features of programming languages is their ability to take small building blocks and compose them (solving big problems by taking small steps at a time). For example, we know how to multiply integers and we know how to output values. It turns out we can do both at the same time:
std::cout << 17 * 3;
Actually, we shouldn't say "at the same time," since in reality the multiplication has to happen before the output. The point is that any expression involving numbers, characters, and variables can be used inside an output statement. We've already seen one example:
std::cout << hour * 60 + minute << std::endl;
You can also put arbitrary expressions on the right-hand side of an assignment statement:
int percentage;
percentage = ( minute * 100 ) / 60;
This ability may not seem so impressive now, but we will see other examples where composition makes it possible to express complex computations neatly and concisely.
The following is illegal:
minute+1 = hour;
The exact rule for what can go on the left-hand side of an assignment expression is not so simple as it was in C; as operator overloading and reference types can complicate the picture.
Chaining
[edit | edit source]std::cout << "The sum of " << a << " and " << b << " is " << sum << "\n";
The above line illustrates what is called chaining of insertion operators to print multiple expressions. How this works is as follows:
- The leftmost insertion operator takes as its operands, std::cout and the string "The sum of ", it prints the latter using the former, and returns a reference to the former.
- Now std::cout << a is evaluated. This prints the value contained in the location a, i.e. 123 and again returns std::cout.
- This process continues. Thus, successively the expressions std::cout << " and ", std::cout << b, std::cout << " is ", std::cout << " sum ", std::cout << "\n" are evaluated and the whole series of chained values is printed.
Table of operators
[edit | edit source]Operators in the same group have the same precedence and the order of evaluation is decided by the associativity (left-to-right or right-to-left). Operators in a preceding group have higher precedence than those in a subsequent group.
| Operators | Description | Example Usage | Associativity |
|---|---|---|---|
| Scope Resolution Operator | — | ||
| :: | unary scope resolution operator for globals |
::NUM_ELEMENTS | |
| :: | binary scope resolution operator for class and namespace members |
std::cout | |
| Function Call, Member Access, Post-Increment/Decrement Operators, RTTI and C++ Casts | Left to right | ||
| () | function call operator | swap (x, y) | |
| [] | array index operator | arr [i] | |
| . | member access operator for an object of class/union type or a reference to it |
obj.member | |
| -> | member access operator for a pointer to an object of class/union type |
ptr->member | |
| ++ -- | post-increment/decrement operators | num++ | |
| typeid() | run time type identification operator for an object or type |
typeid (std::cout) typeid (std::iostream) | |
static_cast<>()dynamic_cast<>()const_cast<>()reinterpret_cast<>()
|
C++ style cast operators for compile-time type conversion See Type Casting for more info |
static_cast<float> (i)dynamic_cast<std::istream> (stream)const_cast<char*> ("Hello, World!")reinterpret_cast<const long*> ("C++")
| |
| type() | functional cast operator ( static_cast is preferredfor conversion to a primitive type) |
float (i) | |
| also used as a constructor call for creating a temporary object, esp. of a class type |
std::string ("Hello, world!", 0, 5) | ||
| Unary Operators | Right to left | ||
| !, not | logical not operator | !eof_reached | |
| ~, compl | bitwise not operator | ~mask | |
| + - | unary plus/minus operators | -num | |
| ++ -- | pre-increment/decrement operators | ++num | |
| &, bitand | address-of operator | &data | |
| * | indirection operator | *ptr | |
| new new[] new() new()[] |
new operators for single objects or arrays |
new std::string (5, '*') new int [100] new (raw_mem) int new (arg1, arg2) int [100] | |
| delete delete[] |
delete operator for pointers to single objects or arrays |
delete ptr delete[] arr | |
sizeofsizeof() |
sizeof operator for expressions or types |
sizeof 123sizeof (int)
| |
| (type) | C-style cast operator (deprecated) | (float)i | |
| Member Pointer Operators | Right to left | ||
| .* | member pointer access operator for an object of class/union type or a reference to it |
obj.*memptr | |
| ->* | member pointer access operator for a pointer to an object of class/union type |
ptr->*memptr | |
| Multiplicative Operators | Left to right | ||
| * / % | multiplication, division and modulus operators |
celsius_diff * 9 / 5 | |
| Additive Operators | Left to right | ||
| + - | addition and subtraction operators | end - start + 1 | |
| Bitwise Shift Operators | Left to right | ||
| << >> |
left and right shift operators | bits << shift_len bits >> shift_len | |
| Relational Inequality Operators | Left to right | ||
| < > <= >= | less-than, greater-than, less-than or equal-to, greater-than or equal-to |
i < num_elements | |
| Relational Equality Operators | Left to right | ||
| == !=, not_eq | equal-to, not-equal-to | choice != 'n' | |
| Bitwise And Operator | Left to right | ||
| &, bitand | bits & clear_mask_complement | ||
| Bitwise Xor Operator | Left to right | ||
| ^, xor | bits ^ invert_mask | ||
| Bitwise Or Operator | Left to right | ||
| |, bitor | bits | set_mask | ||
| Logical And Operator | Left to right | ||
| &&, and | arr != 0 && arr->len != 0 | ||
| Logical Or Operator | Left to right | ||
| ||, or | arr == 0 || arr->len == 0 | ||
| Conditional Operator | Right to left | ||
| ?: | size >= 0 ? size : 0 | ||
| Assignment Operators | Right to left | ||
| = | assignment operator | i = 0 | |
| += -= *= /= %= &=, and_eq |=, or_eq ^=, xor_eq <<= >>= |
shorthand assignment operators (foo op= bar represents foo = foo op bar) |
num /= 10 | |
| Exceptions | — | ||
| throw | throw "Array index out of bounds" | ||
| Comma Operator | Left to right | ||
| , | i = 0, j = i + 1, k = 0 | ||
Assignment
[edit | edit source]The most basic assignment operator is the "=" operator. It assigns one variable to have the value of another. For instance, the statement x = 3 assigns x the value of 3, and y = x assigns whatever was in x to be in y. When the "=" operator is used to assign a class or struct it acts as if the "=" operator was applied on every single element. For instance:
//Example to demonstrate default "=" operator behavior.
struct A
{
int i;
float f;
A * next_a;
};
//Inside some function
{
A a1, a2; // Create two A objects.
a1.i = 3; // Assign 3 to i of a1.
a1.f = 4.5; // Assign the value of 4.5 to f in a1
a1.next_a = &a2; // a1.next_a now points to a2
a2.next_a = NULL; // a2.next_a is guaranteed to point at nothing now.
a2.i = a1.i; // Copy over a1.i, so that a2.i is now 3.
a1.next_a = a2.next_a; // Now a1.next_a is NULL
a2 = a1; // Copy a1 to a2, so that now a2.f is 4.5. The other two are unchanged, since they were the same.
}
Assignments can also be chained since the assignment operator returns the value it assigns. This time the chaining is from right to left. For example, to assign the value of z to y and assign the same value (which is returned by the = operator) to x you use:
x = y = z;
When the "=" operator is used in a declaration it has special meaning. It tells the compiler to directly initialize the variable from whatever is on the right-hand side of the operator. This is called defining a variable, in the same way that you define a class or a function. With classes, this can make a difference, especially when assigning to a function call:
class A { /* ... */ };
A foo () { /* ... */ };
// In some function
{
A a;
a = foo();
A a2 = foo();
}
In the first case, a is constructed, then is changed by the "=" operator. In the second statement, a2 is constructed directly from the return value of foo(). In many cases, the compiler can save a lot of time by constructing foo()'s return value directly into a2's memory, which makes the program run faster.
Whether or not you define can also matter in a few cases where a definition can result in different linkage, making the variable more or less available to other source files.
Arithmetic operators
[edit | edit source]Arithmetic operations that can be performed on integers (also common in many other languages) include:
- Addition, using the
+operator - Subtraction, using the
-operator - Multiplication, using the
*operator - Division, using the
/operator - Remainder, using the
%operator
Consider the next example. It will perform an addition and show the result:
#include<iostream>
using namespace std;
int main()
{
int a = 3, b = 5;
cout << a << '+' << b << '=' << (a+b);
return 0;
}
The line relevant for the operation is where the + operator adds the values stored in the locations a and b. a and b are said to be the operands of +. The combination a + b is called an expression, specifically an arithmetic expression since + is an arithmetic operator.
Addition, subtraction, and multiplication all do what you expect, but you might be surprised by division. For example, the following program:
int hour, minute;
hour = 11;
minute = 59;
std::cout << "Number of minutes since midnight: ";
std::cout << hour*60 + minute << std::endl;
std::cout << "Fraction of the hour that has passed: ";
std::cout << minute/60 << std::endl;
would generate the following output:
Number of minutes since midnight: 719
Fraction of the hour that has passed: 0
The first line is what we expected, but the second line is odd. The value of the variable minute is 59, and 59 divided by 60 is 0.98333, not 0. The reason for the discrepancy is that C++ is performing integer division.
When both of the operands are integers (operands are the things operators operate on) the result must also be an integer, and by definition integer division always rounds down even in cases like this where the next integer is so close.
A possible alternative in this case is to calculate a percentage rather than a fraction:
std::cout << "Percentage of the hour that has passed: ";
std::cout << minute*100/60 << std::endl;
The result is:
Percentage of the hour that has passed: 98
Again the result is rounded down, but at least now the answer is approximately correct. In order to get an even more accurate answer we could use a different type of variable, called floating-point, that is capable of storing fractional values.
This next example:
#include<iostream>
using namespace std;
int main()
{
int a = 33, b = 5;
cout << "Quotient = " << a / b << endl;
cout << "Remainder = "<< a % b << endl;
return 0;
}
will return:
Quotient = 6 Remainder = 3
The multiplicative operators *, / and % are always evaluated before the additive operators + and -. Among operators of the same class, evaluation proceeds from left to right. This order can be overridden using grouping by parentheses, ( and ); the expression contained within parentheses is evaluated before any other neighboring operator is evaluated. But note that some compilers may not strictly follow these rules when they try to optimize the code being generated, unless violating the rules would give a different answer.
For example the following statements convert a temperature expressed in degrees Celsius to degrees Fahrenheit and vice versa:
deg_f = deg_c * 9 / 5 + 32;
deg_c = ( deg_f - 32 ) * 5 / 9;
Compound assignment
[edit | edit source]One of the most common patterns in software with regards to operators is to update a value:
a = a + 1; //Increases a by 1
b = b * 2; //Multiplies b by 2
c = c / 4; //Divides c by 4
Since this pattern is used many times, there is a shorthand for it called compound assignment operators. They are a combination of an existing arithmetic operator and assignment operator:
- +=
- -=
- *=
- /=
- %=
- <<=
- >>=
- |=
- &=
- ^=
Thus the example given in the beginning of the section could be rewritten as
a += 1; // Equivalent to (a = a + 1)
b *= 2; // Equivalent to (b = b * 2)
c /= 4; // Equivalent to (c = c / 4)
Pre and Post Increment
[edit | edit source]Another common pattern is to increase or decrease a value by just 1. This is often used to keep a count of how many times the code has run:
- a++
- a--
- ++a
- --a
- count++
We can again use the previous example and rewrite it as:
a++ // Equivalent to both (a = a + 1) and a += 1
a-- // Equivalent to both (a = a - 1) and a -= 1
However, while "a++" and "++a" look similar, they can result in different values. Post Increment:
a++ // Increments after processing the current statement
Pre Increment:
++a // Increments before processing the current statement
In both examples above, a will be incremented by 1. This may not seem like a big difference, however when used in practice, it may not always be equivalent. For example:
x = 2
a = x++ // a = 2 and x = 3
In the above post increment example, a is assigned to the value of x first, then x is incremented. Since we know that x is 2, a is then assigned the value of 2, afterwards, x is incremented to 3.
x = 2
a = ++x // a = 3 and x = 3
In the above pre increment example, x is incremented and a is assigned to the incremented value. Since we know that x is 2, and it is being incremented by 1, a is assigned the value of 3, and x has been incremented to 3.
Character operators
[edit | edit source]Interestingly, the same mathematical operations that work on integers also work on characters.
char letter;
letter = 'a' + 1;
std::cout << letter << std::endl;
For the above example, outputs the letter b (on most systems -- note that C++ doesn't assume use of ASCII, EBCDIC, Unicode etc. but rather allows for all of these and other charsets). Although it is syntactically legal to multiply characters, it is almost never useful to do it.
Earlier I said that you can only assign integer values to integer variables and character values to character variables, but that is not completely true. In some cases, C++ converts automatically between types. For example, the following is legal.
int number;
number = 'a';
std::cout << number << std::endl;
On most mainstream desktop computers the result is 97, which is the number that is used internally by C++ on that system to represent the letter 'a'. However, it is generally a good idea to treat characters as characters, and integers as integers, and only convert from one to the other if there is a good reason. Unlike some other languages, C++ does not make strong assumptions about how the underlying platform represents characters; ASCII, EBCDIC and others are possible, and portable code will not make assumptions (except that '0', '1', ..., '9' are sequential, so that e.g. '9'-'0' == 9).
Automatic type conversion is an example of a common problem in designing a programming language, which is that there is a conflict between formalism, which is the requirement that formal languages should have simple rules with few exceptions, and convenience, which is the requirement that programming languages be easy to use in practice.
More often than not, convenience wins, which is usually good for expert programmers, who are spared from rigorous but unwieldy formalism, but bad for beginning programmers, who are often baffled by the complexity of the rules and the number of exceptions. In this book I have tried to simplify things by emphasizing the rules and omitting many of the exceptions.
Bitwise operators
[edit | edit source]These operators deal with a bitwise operations. Bit operations needs the understanding of binary numeration since it will deal with on one or two bit patterns or binary numerals at the level of their individual bits. On most microprocessors, bitwise operations are sometimes slightly faster than addition and subtraction operations and usually significantly faster than multiplication and division operations.
Bitwise operations especially important for much low-level programming from optimizations to writing device drivers, low-level graphics, communications protocol packet assembly and decoding.
Although machines often have efficient built-in instructions for performing arithmetic and logical operations, in fact all these operations can be performed just by combining the bitwise operators and zero-testing in various ways.
The bitwise operators work bit by bit on the operands. The operands must be of integral type (one of the types used for integers).
For this section, recall that a number starting with 0x is hexadecimal (hexa, or hex for short or referred also as base-16). Unlike the normal decimal system using powers of 10 and the digits 0123456789, hex uses powers of 16 and the symbols 0123456789abcdef. In the examples remember that Oxc equals 1100 in binary and 12 in decimal. C++ does not directly support binary notation, which would hamper readability of the code.
- NOT
- ~a
- bitwise complement of a.
- ~0xc produces the value -1-0xc (in binary, ~1100 produces ...11110011 where "..." may be many more 1 bits)
The negation operator is a unary operator which precedes the operand, This operator must not be confused with the "logical not" operator, "!" (exclamation point), which treats the entire value as a single Boolean—changing a true value to false, and vice versa. The "logical not" is not a bitwise operation.
These others are binary operators which lie between the two operands. The precedence of these operators is lower than that of the relational and equivalence operators; it is often required to parenthesize expressions involving bitwise operators.
- AND
- a & b
- bitwise boolean and of a and b
- 0xc & 0xa produces the value 0x8 (in binary, 1100 & 1010 produces 1000)
The truth table of a AND b:
| a | b | ∧ |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
- OR
- a | b
- bitwise boolean or of a and b
- 0xc | 0xa produces the value 0xe (in binary, 1100 | 1010 produces 1110)
The truth table of a OR b is:
| a | b | ∨ |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
- XOR
- a ^ b
- bitwise xor of a and b
- 0xc ^ 0xa produces the value 0x6 (in binary, 1100 ^ 1010 produces 0110)
The truth table of a XOR b:
| a | b | ⊕ |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
- Bit shifts
- a << b
- shift a left by b (multiply a by )
- 0xc << 1 produces the value 0x18 (in binary, 1100 << 1 produces the value 11000)
- a >> b
- shift a right by b (divide a by )
- 0xc >> 1 produces the value 0x6 (in binary, 1100 >> 1 produces the value 110)
Derived types operators
[edit | edit source]There are three data types known as pointers, references, and arrays, that have their own operators for dealing with them. Those are *, &, [], ->, .*, and ->*.
Pointers, references, and arrays are fundamental data types that deal with accessing other variables. Pointers are used to pass around a variables address (where it is in memory), which can be used to have multiple ways to access a single variable. References are aliases to other objects, and are similar in use to pointers, but still very different. Arrays are large blocks of contiguous memory that can be used to store multiple objects of the same type, like a sequence of characters to make a string.
Subscript operator [ ]
[edit | edit source]This operator is used to access an object of an array. It is also used when declaring array types, allocating them, or deallocating them.
Arrays
[edit | edit source]An array stores a constant-sized sequential set of blocks, each block containing a value of the selected type under a single name. Arrays often help organize collections of data efficiently and intuitively.
It is easiest to think of an array as simply a list with each value as an item of the list. Where individual elements are accessed by their position in the array called its index, also known as subscript. Each item in the array has an index from 0 to (the size of the array) -1, indicating its position in the array.
Advantages of arrays include:
- Random access in O(1) (Big O notation)
- Ease of use/port: Integrated into most modern languages
Disadvantages include:
- Constant size
- Constant data-type
- Large free sequential block to accommodate large arrays
- When used as non-static data members, the element type must allow default construction
- Arrays do not support copy assignment (you cannot write
arraya = arrayb) - Arrays cannot be used as the value type of a standard container
- Syntax of use differs from standard containers
- Arrays and inheritance don't mix (an array of Derived is not an array of Base, but can too easily be treated like one)
For example, here is an array of integers, called List with 5 elements, numbered 0 to 4. Each element of the array is an integer. Like other integer variables, the elements of the array start out uninitialized. That means it is filled with unknown values until we initialize it by assigning something to it. (Remember primitive types in C are not initialized to 0.)
| Index | Data |
| 00 | unspecified |
| 01 | unspecified |
| 02 | unspecified |
| 03 | unspecified |
| 04 | unspecified |
Since an array stores values, what type of values and how many values to store must be defined as part of an array declaration, so it can allocate the needed space. The size of array must be a const integral expression greater than zero. That means that you cannot use user input to declare an array. You need to allocate the memory (with operator new[]), so the size of an array has to be known at compile time. Another disadvantage of the sequential storage method is that there has to be a free sequential block large enough to hold the array. If you have an array of 500,000,000 blocks, each 1 byte long, you need to have roughly 500 megabytes of sequential space to be free; Sometimes this will require a defragmentation of the memory, which takes a long time.
To declare an array you can do:
int numbers[30]; // creates an array of 30 integers
or
char letters[4]; // create an array of 4 characters
and so on...
to initialize as you declare them you can use:
int vector[6]={0,0,1,0,0,0};
this will not only create the array with 6 int elements but also initialize them to the given values.
If you initialize the array with less than the full number of elements, the remaining elements are set to a default value - zero in the case of numbers.
int vector[6]={0,0,1}; // this is the same as the example above
If you fully initialize the array as you declare it, you can allow the compiler to work out the size of the array:
int vector[]={0,0,1,0,0,0}; // the compiler can see that there are 6 elements
Assigning and accessing data
[edit | edit source]You can assign data to the array by using the name of the array, followed by the index.
For example to assign the number 200 into the element at index 2 in the array
List[2] = 200;
will give
| Index | Data |
| 00 | unspecified |
| 01 | unspecified |
| 02 | 200 |
| 03 | unspecified |
| 04 | unspecified |
You can access the data at an element of the array the same way.
std::cout << List[2] << std::endl;
This will print 200.
Basically working with individual elements in an array is no different then working with normal variables.
As you see accessing a value stored in an array is easy. Take this other example:
int x;
x = vector[2];
The above declaration will assign x the valued store at index 2 of variable vector which is 1.
Arrays are indexed starting at 0, as opposed to starting at 1. The first element of the array above is vector[0]. The index to the last value in the array is the array size minus one. In the example above the subscripts run from 0 through 5. C++ does not do bounds checking on array accesses. The compiler will not complain about the following:
char y;
int z = 9;
char vector[6] = { 1, 2, 3, 4, 5, 6 };
// examples of accessing outside the array. A compile error is not raised
y = vector[15];
y = vector[-4];
y = vector[z];
During program execution, an out of bounds array access does not always cause a run time error. Your program may happily continue after retrieving a value from vector[-1]. To alleviate indexing problems, the sizeof expression is commonly used when coding loops that process arrays.
int ix;
short anArray[]= { 3, 6, 9, 12, 15 };
for (ix=0; ix< (sizeof(anArray)/sizeof(short)); ++ix) {
DoSomethingWith( anArray[ix] );
}
Notice in the above example, the size of the array was not explicitly specified. The compiler knows to size it at 5 because of the five values in the initializer list. Adding an additional value to the list will cause it to be sized to six, and because of the sizeof expression in the for loop, the code automatically adjusts to this change.
multidimensional arrays
[edit | edit source]You can also use multi-dimensional arrays. The simplest type is a two dimensional array. This creates a rectangular array - each row has the same number of columns. To get a char array with 3 rows and 5 columns we write...
char two_d[3][5];
To access/modify a value in this array we need two subscripts:
char ch;
ch = two_d[2][4];
or
two_d[0][0] = 'x';
example
[edit | edit source]There are also weird notations possible:
int a[100];
int i = 0;
if (a[i]==i[a])
printf("Hello World!\n");
a[i] and i[a] point to the same location. You will understand this better after knowing about pointers.
To get an array of a different size, you must explicitly deal with memory using realloc, malloc, memcpy, etc.
Why start at 0?
[edit | edit source]Most programming languages number arrays from 0. This is useful in languages where arrays are used interchangeably with a pointer to the first element of the array. In C++ the address of an element in the array can be computed from (address of first element) + i, where i is the index starting at 0 (a[1] == *(a + 1)). Notice here that "(address of the first element) + i" is not a literal addition of numbers. Different types of data have different sizes and the compiler will correctly take this into account. Therefore, it is simpler for the pointer arithmetic if the index started at 0.
Why no bounds checking on array indexes?
[edit | edit source]C++ does allow for, but doesn't force, bounds-checking implementations, in practice little or no checking is done. It affects storage requirements (needing "fat pointers") and impacts runtime performance. However, the std::vector template class, that we mentioned and we will examine later in greater detail (a template class container, representing an array provides the at() method) which does enforce bounds checking. Also in many implementations, the standard containers include particularly complete bounds checking in debug mode. They might not support these checks in release builds, as any performance reduction in container classes relative to built-in arrays might prevent programmers from migrating from arrays to the more modern, safer container classes.
address-of operator &
[edit | edit source]To get the address of a variable so that you can assign a pointer, you use the "address of" operator, which is denoted by the ampersand & symbol. The "address of" operator does exactly what it says, it returns the "address of" a variable, a symbolic constant, or a element in an array, in the form of a pointer of the corresponding type. To use the "address of" operator, you tack it on in front of the variable that you wish to have the address of returned. It is also used when declaring reference types.
Now, do not confuse the "address of" operator with the declaration of a reference. Because use of operators is restricted to expression, the compiler knows that &sometype is the "address of" operator being used to denote the return of the address of sometype as a pointer.
References
[edit | edit source]References are a way of assigning a "handle" to a variable. References can also be thought of as "aliases"; they're not real objects, they're just alternative names for other objects.
- Assigning References
- This is the less often used variety of references, but still worth noting as an introduction to the use of references in function arguments. Here we create a reference that looks and acts like a standard variable except that it operates on the same data as the variable that it references.
int tZoo = 3; // tZoo == 3
int &refZoo = tZoo; // tZoo == 3
refZoo = 5; // tZoo == 5
refZoo is a reference to tZoo. Changing the value of refZoo also changes the value of tZoo.
For example say we want to have a function to swap 2 integers
void swap(int &a, int &b){
int temp = a;
a = b;
b = temp;
}
int main(){
int x = 5;
int y = 6;
int &refx = x;
int &refy = y;
swap(refx, refy); // now x = 6 and y = 5
swap(x, y); // and now x = 5 and y = 6 again
}
References cannot be null as they refer to instantiated objects, while pointers can be null. References cannot be reassigned, while pointers can be.
int main(){
int x = 5;
int y = 6;
int &refx = x;
&refx = y; // won't compile
}
As references provide strong guarantees when compared with pointers, using references makes the code simpler. Therefore using references should usually be preferred over using pointers. Of course, pointers have to be used at the time of dynamic memory allocation (new) and deallocation (delete).
Pointers, Operator *
[edit | edit source]The * operator is used when declaring pointer types but it is also used to get the variable pointed to by a pointer.
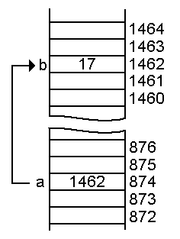
Pointers are important data types due to special characteristics. They may be used to indicate a variable without actually creating a variable of that type. Because they can be a difficult concept to understand, some special effort should be spent on understanding the power they give to programmers.
Pointers have a very descriptive name. Pointers variables only store memory addresses, usually the addresses of other variables. Essentially, they point to another variable's memory location, a reserved location on the computer memory. You can use a pointer to pass the location of a variable to a function, this enables the function's pointer to use the variable space, so that it can retrieve or modify its data. You can even have pointers to pointers, and pointers to pointers to pointers and so on and so forth.
Declaring
[edit | edit source]Pointers are declared by adding a * before the variable name in the declaration, as in the following example:
int* x; // pointer to int.
int * y; // pointer to int. (legal, but rarely used)
int *z; // pointer to int.
int*i; // pointer to int. (legal, but rarely used)
Watch out, though, because the * associates to the following declaration only:
int* i, j; // CAUTION! i is pointer to int, j is int.
int *i, *j; // i and j are both pointer to int.
You can also have multiple pointers chained together, as in the following example:
int **i; // Pointer to pointer to int.
int ***i; // Pointer to pointer to pointer to int (rarely used).
Assigning values
[edit | edit source]Everyone gets confused about pointers as assigning values to pointers may be a bit tricky, but if you know the basics, you can proceed more easily. By carefully going through the examples rather than a simple description, try to understand the points as they are presented to you.
- Assigning values to pointers (non-char type)
double vValue = 25.0;// declares and initializes a vValue as type double
double* pValue = &vValue;
cout << *pValue << endl;
The second statement uses "&" the reference operator and "*" to tell the compiler this is a pointer variable and assign vValue variable's address to it. In the last statement, it outputs the value from the vValue variable by de-referencing the pointer using the "*" operator.
- Assigning values to pointers (char type)
char pArray[20] = {"Name1"};
char* pValue(pArray);// or 0 in old compilers, nullptr is a part of C++0X
pValue = "Value1";
cout << pValue << endl ;// this will return the Value1;
So as mentioned early, a pointer is a variable which stores the address of another variable, as you need to initialize an array because you can not directly assign values to it. You will need to use pointers directly or a pointer to array in a mixed context, to use pointers alone, examine the next example.
char* pValue("String1");
pValue = "String2";
cout << pValue << endl ;
Remember you can't leave the pointer alone or initialize it as nullptr cause it will case an error. The compiler thinks it is as a memory address holder variable since you didn't point to anything and will try to assign values to it, that will cause an error since it does not point to anywhere.
Dereferencing
[edit | edit source]This is the * operator. It is used to get the variable pointed to by a pointer. It is also used when declaring pointer types.
When you have a pointer, you need some way to access the memory that it points to. When it is put in front of a pointer, it gives the variable pointed to. This is an lvalue, so you can assign values to it, or even initialize a reference from it.
#include <iostream>
int main()
{
int i;
int * p = &i;
i = 3;
std::cout<<*p<<std::endl; // prints "3"
return 0;
}
Since the result of an & operator is a pointer, *&i is valid, though it has absolutely no effect.
Now, when you combine the * operator with classes, you may notice a problem. It has lower precedence than .! See the example:
struct A { int num; };
A a;
int i;
A * p;
p = &a;
a.num = 2;
i = *p.num; // Error! "p" isn't a class, so you can't use "."
i = (*p).num;
The error happens because the compiler looks at p.num first ("." has higher precedence than "*") and because p does not have a member named num the compiler gives you an error. Using grouping symbols to change the precedence gets around this problem.
It would be very time-consuming to have to write (*p).num a lot, especially when you have a lot of classes. Imagine writing (*(*(*(*MyPointer).Member).SubMember).Value).WhatIWant! As a result, a special operator, ->, exists. Instead of (*p).num, you can write p->num, which is completely identical for all purposes. Now you can write MyPointer->Member->SubMember->Value->WhatIWant. It's a lot easier on the brain!
Null pointer
[edit | edit source]The null pointer is a special status of pointers. It means that the pointer points to absolutely nothing. It is an error to attempt to dereference (using the * or -> operators) a null pointer. A null pointer can be referred to using the constant zero, as in the following example:
int i;
int *p;
p = 0; //Null pointer.
p = &i; //Not the null pointer.
Note that you can't assign a pointer to an integer, even if it's zero. It has to be the constant. The following code is an error:
int i = 0;
int *p = i; //Error: 0 only evaluates to null if it's a pointer
There is an old macro, defined in the standard library, derived from the C language that inconsistently has evolved into #define NULL ((void *)0), this makes NULL, always equal to a null pointer value (essentially, 0).
Since a null pointer is 0, it will always compare to 0. Like an integer, if you use it in a true/false expression, it will return false if it is the null pointer, and true if it's anything else:
#include <iostream>
void IsNull (int * p)
{
if (p)
std::cout<<"Pointer is not NULL"<<std::endl;
else
std::cout<<"Pointer is NULL"<<std::endl;
}
int main()
{
int * p;
int i;
p = NULL;
IsNull(p);
p = &i;
IsNull(&i);
IsNull(p);
IsNull(NULL);
return 0;
}
This program will output that the pointer is NULL, then that it isn't NULL twice, then again that it is.
Pointers and multidimensional arrays
[edit | edit source]- Pointers and Multidimensional non-Char Arrays
A working knowledge of how to initialize two dimensional arrays, assign values to arrays, and return values from arrays is necessary. In depth information about arrays can be found in section 1.4.10.1.1 Arrays. However, when relevant to the understanding of pointers, arrays will be mentioned here, as well.
- The main objects are
- Assign Values to Multidimensional Pointers
- How to use Pointers with Multidimensional Arrays
- Return Values
- Initialize Pointers and Arrays
- How to Arrange Values in them
- Assign Values to Multidimensional Pointers.
In non-Char Type you need to involve arrays with Pointers since Pointers treat char* type to in special way and other type to another way like only refer the address or get the address and get the value by indirect method.
If you declare it like this way:
double (*pDVal)[2] = {{1,2},{1,2}};
It will probably generate an error! Because pointers used in non-Char type only directly, in char types refer the address of another variable by assigning a variable first then you can get its (that assigned variable) value indirectly!
double ArrayVal[5][5] = {
{1,2,3,4,5},
{1,2,3,4,5},
{1,2,3,4,5},
{1,2,3,4,5},
{1,2,3,4,5},
};
double(*pArray)[5] = ArrayVal;
*(*(pArray+0)+0) = 10;
*(*(pArray+0)+1) = 20;
*(*(pArray+0)+2) = 30;
*(*(pArray+0)+3) = 40;
*(*(pArray+0)+4) = 50;
*(*(pArray+1)+0) = 60;
*(*(pArray+1)+1) = 70;
*(*(pArray+1)+2) = 80;
*(*(pArray+1)+3) = 90;
*(*(pArray+1)+4) = 100;
*(*(pArray+2)+0) = 110;
*(*(pArray+2)+1) = 120;
*(*(pArray+2)+2) = 130;
*(*(pArray+2)+3) = 140;
*(*(pArray+2)+4) = 150;
*(*(pArray+3)+0) = 160;
*(*(pArray+3)+1) = 170;
*(*(pArray+3)+2) = 180;
*(*(pArray+3)+3) = 190;
*(*(pArray+3)+4) = 200;
*(*(pArray+4)+0) = 210;
*(*(pArray+4)+1) = 220;
*(*(pArray+4)+2) = 230;
*(*(pArray+4)+3) = 240;
*(*(pArray+4)+4) = 250;
There is another way instead
*(*(pArray+0)+0)
it is
*(pArray[0]+0)
You can use one of them to assign value to Array through the pointer to return values you can use either the appropriate Array or Pointer.
- Pointers and multidimensional char arrays
This is bit hard and even hard to remember so I suggest keep practicing until you get the spirit of Pointers only! You cannot use Pointers + Multidimensional Arrays with Char Type. Only for non-char type.
- Multidimensional pointer with char type
char* pVar[5] = { "Name1" , "Name2" , "Name3", "Name4", "Name5" }
pVar[0] = "XName01";
cout << pVar[0] << endl ; //this will return the XName01 instead Name1 which was replaced with Name1.
here the 5 in the first statement is the number of rows (no columns need to be specified in pointer it is only in Arrays) the next statement assigns another string to position 0 which is the position of first place of first statement. finally return the answer
- Dynamic memory allocation
In your system memory each memory block got an address so whenever you compile the code at the beginning all variable reserve some space in the memory but in Dynamic Memory Allocation it only reserve when it needed it means at execution time of that statement this allocates memory in your free space area(unused space) so it means if there is no space or no contiguous blocks then the compiler will generate and error message
- Dynamic memory allocation and pointer non-char type
This is same as assign non-char 1 dimensional Array to Pointer
double* pVal = new double[5];
//or double* pVal = new double; // this line leaves out the necessary memory allocation
*(pVal+0) = 10;
*(pVal+1) = 20;
*(pVal+2) = 30;
*(pVal+3) = 40;
*(pVal+4) = 50;
cout << *(pVal+0) << endl;
The first statement's Lside(left side) declares an variable and Rside request a space for double type variable and allocate it in free space area in your memory. So next and so fourth you can see it increases the integer value that means *(pVal+0) pVal -> if this uses alone it will return the address corresponding to first memory block. (that used to store the 10) and 0 means move 0 block ahead but its 0 means do not move stay in current memory block, and you use () parenthesis because + < * < () consider the priority so you need to use parenthesis avoid to calculating the * first
- is called INDIRECT Operator which DE-REFERENCE THE Pointer and return the value corresponding to the memory block.
(Memory Block Address+steps)
- -> De-reference.
- Dynamic memory allocation and pointer char type
char* pVal = new char;
pVal = "Name1";
cout << pVal << endl;
delete pVal; //this will delete the allocated space
pVal = nullptr //null the pointer
You can see this is the same as static memory declaration, in static declaration it goes:
char* pVal("Name1");
- Dynamic memory allocation and pointer non-char array type
double (*pVal2)[2]= new double[2][2]; //this will add 2x2 memory blocks to type double pointer
*(*(pVal2+0)+0) = 10;
*(*(pVal2+0)+1) = 10;
*(*(pVal2+0)+2) = 10;
*(*(pVal2+0)+3) = 10;
*(*(pVal2+0)+4) = 10;
*(*(pVal2+1)+0) = 10;
*(*(pVal2+1)+1) = 10;
*(*(pVal2+1)+2) = 10;
*(*(pVal2+1)+3) = 10;
*(*(pVal2+1)+4) = 10;
delete [] pVal; //the dimension does not matter; you only need to mention []
pVal = nullptr
Pointers to classes
[edit | edit source]Indirection operator ->
[edit | edit source]This pointer indirection operator is used to access a member of a class pointer.
Member dereferencing operator .*
[edit | edit source]This pointer-to-member dereferencing operator is used to access the variable associated with a specific class instance, given an appropriate pointer.
Member indirection operator ->*
[edit | edit source]This pointer-to-member indirection operator is used to access the variable associated with a class instance pointed to by one pointer, given another pointer-to-member that's appropriate.
Pointers to functions
[edit | edit source]When used to point to functions, pointers can be exceptionally powerful. A call can be made to a function anywhere in the program, knowing only what kinds of parameters it takes. Pointers to functions are used several times in the standard library, and provide a powerful system for other libraries which need to adapt to any sort of user code. This case is examined more in depth in the Functions Section of this book.
The sizeof keyword refers to an operator that works at compile time to report on the size of the storage occupied by a type of the argument passed to it (equivalently, by a variable of that type). That size is returned as a multiple of the size of a char, which on many personal computers is 1 byte (or 8 bits). The number of bits in a char is stored in the CHAR_BIT constant defined in the <climits> header file. This is one of the operators for which operator overloading is not allowed.
//Examples of sizeof use
int int_size( sizeof( int ) );// Might give 1, 2, 4, 8 or other values.
// or
int answer( 42 );
int answer_size( sizeof( answer ) );// Same value as sizeof( int )
int answer_size( sizeof answer); // Equivalent syntax
For example, the following code uses sizeof to display the sizes of a number of variables:
struct EmployeeRecord {
int ID;
int age;
double salary;
EmployeeRecord* boss;
};
//...
cout << "sizeof(int): " << sizeof(int) << endl
<< "sizeof(float): " << sizeof(float) << endl
<< "sizeof(double): " << sizeof(double) << endl
<< "sizeof(char): " << sizeof(char) << endl
<< "sizeof(EmployeeRecord): " << sizeof(EmployeeRecord) << endl;
int i;
float f;
double d;
char c;
EmployeeRecord er;
cout << "sizeof(i): " << sizeof(i) << endl
<< "sizeof(f): " << sizeof(f) << endl
<< "sizeof(d): " << sizeof(d) << endl
<< "sizeof(c): " << sizeof(c) << endl
<< "sizeof(er): " << sizeof(er) << endl;
On most machines (considering the size of char), the above code displays this output:
sizeof(int): 4
sizeof(float): 4
sizeof(double): 8
sizeof(char): 1
sizeof(EmployeeRecord): 20
sizeof(i): 4
sizeof(f): 4
sizeof(d): 8
sizeof(c): 1
sizeof(er): 20
It is also important to note that the sizes of various types of variables can change depending on what system you're on. Check the data types page for more information.
Syntactically, sizeof appears like a function call when taking the size of a type, but may be used without parentheses when taking the size of a variable type (e.g. sizeof(int)). Parentheses can be left out if the argument is a variable or array (e.g. sizeof x, sizeof myArray). Style guidelines vary on whether using the latitude to omit parentheses in the latter case is desirable.
Consider the next example:
#include <cstdio>
short func( short x )
{
printf( "%d", x );
return x;
}
int main()
{
printf( "%d", sizeof( sizeof( func(256) ) ) );
}
Since sizeof does not evaluate anything at run time, the func() function is never called. All information needed is the return type of the function, the first sizeof will return the size of a short (the return type of the function) as the value 2 (in size_t, an integral type defined in the include file STDDEF.H) and the second sizeof will return 4 (the size of size_t returned by the first sizeof).
sizeof measures the size of an object in the simple sense of a contiguous area of storage; for types which include pointers to other storage, the indirect storage is not included in the value returned by sizeof. A common mistake made by programming newcomers working with C++ is to try to use sizeof to determine the length of a string; the std::strlen or std::string::length functions are more appropriate for that task.
sizeof has also found new life in recent years in template meta programming, where the fact that it can turn types into numbers, albeit in a primitive manner, is often useful, given that the template metaprogramming environment typically does most of its calculations with types.
Dynamic memory allocation
[edit | edit source]Dynamic memory allocation is the allocation of memory storage for use in a computer program during the runtime of that program. It is a way of distributing ownership of limited memory resources among many pieces of data and code. Importantly, the amount of memory allocated is determined by the program at the time of allocation and need not be known in advance. A dynamic allocation exists until it is explicitly released, either by the programmer or by a garbage collector implementation; this is notably different from automatic and static memory allocation, which require advance knowledge of the required amount of memory and have a fixed duration. It is said that an object so allocated has dynamic lifetime.
The task of fulfilling an allocation request, which involves finding a block of unused memory of sufficient size, is complicated by the need to avoid both internal and external fragmentation while keeping both allocation and deallocation efficient. Also, the allocator's metadata can inflate the size of (individually) small allocations; chunking attempts to reduce this effect.
Usually, memory is allocated from a large pool of unused memory area called the heap (also called the free store). Since the precise location of the allocation is not known in advance, the memory is accessed indirectly, usually via a reference. The precise algorithm used to organize the memory area and allocate and deallocate chunks is hidden behind an abstract interface and may use any of the methods described below.
You have probably wondered how programmers allocate memory efficiently without knowing, prior to running the program, how much memory will be necessary. Here is when the fun starts with dynamic memory allocation.
new and delete
[edit | edit source]For dynamic memory allocation we use the new and delete keywords, the old malloc from C functions can now be avoided but are still accessible for compatibility and low level control reasons.
As covered before, we assign values to pointers using the "address of" operator because it returns the address in memory of the variable or constant in the form of a pointer. Now, the "address of" operator is NOT the only operator that you can use to assign a pointer. You have yet another operator that returns a pointer, which is the new operator. The new operator allows the programmer to allocate memory for a specific data type, struct, class, etc., and gives the programmer the address of that allocated sect of memory in the form of a pointer. The new operator is used as an rvalue, similar to the "address of" operator. Take a look at the code below to see how the new operator works.
By assigning the pointers to an allocated sector of memory, rather than having to use a variable declaration, you basically override the "middleman" (the variable declaration). Now, you can allocate memory dynamically without having to know the number of variables you should declare.
int n = 10;
SOMETYPE *parray, *pS;
int *pint;
parray = new SOMETYPE[n];
pS = new SOMETYPE;
pint = new int;
If you looked at the above piece of code, you can use the new operator to allocate memory for arrays too, which comes quite in handy when we need to manipulate the sizes of large arrays and or classes efficiently. The memory that your pointer points to because of the new operator can also be "deallocated," not destroyed but rather, freed up from your pointer. The delete operator is used in front of a pointer and frees up the address in memory to which the pointer is pointing.
delete [] parray;// note the use of [] when destroying an array allocated with new
delete pint;
The memory pointed to by parray and pint have been freed up, which is a very good thing because when you're manipulating multiple large arrays, you try to avoid losing the memory someplace by leaking it. Any allocation of memory needs to be properly deallocated or a leak will occur and your program won't run efficiently. Essentially, every time you use the new operator on something, you should use the delete operator to free that memory before exiting. The delete operator, however, not only can be used to delete a pointer allocated with the new operator, but can also be used to "delete" a null pointer, which prevents attempts to delete non-allocated memory (this action compiles and does nothing).
You must keep in mind that new T and new T() are not equivalent. This will be more understandable after you are introduced to more complex types like classes, but keep in mind that when using new T() it will initialize the T memory location ("zero out") before calling the constructor (if you have non-initialized members variables, they will be initialized by default).
The new and delete operators do not have to be used in conjunction with each other within the same function or block of code. It is proper and often advised to write functions that allocate memory and other functions that deallocate memory. Indeed, the currently favored style is to release resources in object's destructors, using the so-called resource acquisition is initialization (RAII) idiom.
As we will see when we get to the Classes, a class destructor is the ideal location for its deallocator, it is often advisable to leave memory allocators out of classes' constructors. Specifically, using new to create an array of objects, each of which also uses new to allocate memory during its construction, often results in runtime errors. If a class or structure contains members which must be pointed at dynamically-created objects, it is best to sequentially initialize arrays of the parent object, rather than leaving the task to their constructors.
// Example of a dynamic array
const int b = 5;
int *a = new int[b];
//to delete
delete[] a;
The ideal way is to not use arrays at all, but rather the STL's vector type (a container similar to an array). To achieve the above functionality, you should do:
const int b = 5;
std::vector<int> a;
a.resize(b);
//to delete
a.clear();
Vectors allow for easy insertions even when "full." If, for example, you filled up a, you could easily make room for a 6th element like so:
int new_number = 99;
a.push_back( new_number );//expands the vector to fit the 6th element
You can similarly dynamically allocate a rectangular multidimensional array (be careful about the type syntax for the pointers):
const int d = 5;
int (*two_d_array)[4] = new int[d][4];
//to delete
delete[] two_d_array;
You can also emulate a ragged multidimensional array (sub-arrays not the same size) by allocating an array of pointers, and then allocating an array for each of the pointers. This involves a loop.
const int d1 = 5, d2 = 4;
int **two_d_array = new int*[d1];
for( int i = 0; i < d1; ++i)
two_d_array[i] = new int[d2];
//to delete
for( int i = 0; i < d1; ++i)
delete[] two_d_array[i];
delete[] two_d_array;

